مبرهنة كارنو (هندسة رياضية)

في الهندسة الإقليدية، تنص مبرهنة كارنو (بالإنجليزية: Carnot's theorem)‏ نسبةً إلى لازار كارنو (1753 - 1823م) على أنَّ مجموعَ المسافاتِ من مركزِ دائرةِ مثلثِ محيطةِ إلى أضلاعه مساوٍ لمجموع نصفي قطري دائرتيه المُحيطة والداخلية. يُعبّرُ عن ذلكَ رياضياً: إذا كان ${\displaystyle \triangle ABC}$ مثلثاً و${\displaystyle D}$ مركزَ دائرتهِ المحيطة، و${\displaystyle F,G,H}$ هي مساقطها على أضلاعه، فإنَّ:[1]

$${\displaystyle DF+DG+DH=R+r}$$

  ميّز عن مبرهنة كارنو (ديناميكا حرارية).

${\displaystyle {\begin{aligned}&{}\qquad DG+DH+DF\\&{}=|DG|+|DH|-|DF|\\&{}=R+r\end{aligned}}}$

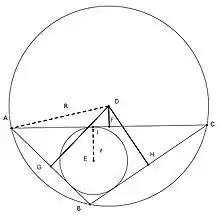
بملاحظة أن المسافات مُتجهة.أي أنها تكونُ سالبةً إذا كانت القطعة المستقيمة ${\displaystyle DX}$ تقع بكاملها خارج المثلث لكل ${\displaystyle X=F,G,H}$. على سبيل المثال، فإنَّ القطعة المستقيمة ${\displaystyle DF}$ تكون ذات طول سالب، والقطعتين المستقيمتين ${\displaystyle DH,DG}$ موجبتان.[1]