34 (number)
34 (thirty-four) is the natural number following 33 and preceding 35.
| ||||
|---|---|---|---|---|
| Cardinal | thirty-four | |||
| Ordinal | 34th (thirty-fourth) | |||
| Factorization | 2 × 17 | |||
| Divisors | 1, 2, 17, 34 | |||
| Greek numeral | ΛΔ´ | |||
| Roman numeral | XXXIV | |||
| Binary | 1000102 | |||
| Ternary | 10213 | |||
| Senary | 546 | |||
| Octal | 428 | |||
| Duodecimal | 2A12 | |||
| Hexadecimal | 2216 | |||
In mathematics
34 is the ninth distinct semiprime,[1] with four divisors including 1 and itself. Specifically, 34 is the ninth distinct semiprime, it being the sixth of the form . Its neighbors 33 and 35 are also distinct semiprimes with four divisors each, where 34 is the smallest number to be surrounded by numbers with the same number of divisors it has. This is the first distinct semiprime treble cluster, the next being (85, 86, 87).[2]

The number 34 has an aliquot sum of 20, and is the seventh member in the aliquot sequence (34, 20, 22, 14, 10, 8, 7, 1, 0) that belongs to the prime 7-aliquot tree.
Its reduced totient and Euler totient values are both 16 (or 42 = 24).[3][4] The sum of all its divisors aside from one equals 53, which is the sixteenth prime number.
There is no solution to the equation φ(x) = 34, making 34 a nontotient.[5] Nor is there a solution to the equation x − φ(x) = 34, making 34 a noncototient.[6]
It is the third Erdős–Woods number, following 22 and 16.[7]
It is the ninth Fibonacci number[8] and a companion Pell number.[9] Since it is an odd-indexed Fibonacci number, 34 is a Markov number.[10]
34 is also the fourth heptagonal number.[11]
This number is also the magic constant of Queens Problem for .[12]
There are 34 topologically distinct convex heptahedra, excluding mirror images.[13]
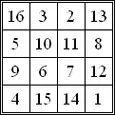
34 is the magic constant of a normal magic square,[14] and magic octagram (see accompanying images).
In science
- The atomic number of selenium
- Potentially one of the magic numbers in physics.[15][16]
- Messier object M34, a magnitude 6.0 open cluster in the constellation Perseus
- The New General Catalogue object NGC 34, a peculiar galaxy in the constellation Cetus
- The human vertebral column is made up of up to 34 vertebrae.[17]
Literature
- In The Count of Monte Cristo, Number 34 is how Edmond Dantès is referred to during his imprisonment in the Château d'If.
Transportation
- 34th Street (Manhattan), a major cross-town street in New York City
- 34th Street (New York City Subway), multiple New York City subway stations
In other fields
34 is also:
- The traffic code of Istanbul, Turkey
- "#34", a song by the Dave Matthews Band
- The number of the French department Hérault
- +34 is the code for international direct-dial phone calls to Spain
- The number used to win the 2021 Daytona 500 with Michael McDowell and Front Row Motorsports. The number and team also won at Pocono Raceway with Chris Buescher and Talladega Superspeedway with David Ragan. In 1961, Wendell Scott won with the number to become the first African American to win in NASCAR.
See also
References
- Sloane, N. J. A. (ed.). "Sequence A001358". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Sloane, N. J. A. (ed.). "Sequence A056809". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Sloane, N. J. A. (ed.). "Sequence A000010 (Euler totient function phi(n): count numbers less than and equal to n and prime to n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-09-11.
- Sloane, N. J. A. (ed.). "Sequence A002322 (Reduced totient function psi(n): least k such that x^k congruent to 1 (mod n) for all x prime to n; also known as the Carmichael lambda function (exponent of unit group mod n); also called the universal exponent of n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-09-11.
- "Sloane's A005277 : Nontotients". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
- "Sloane's A005278 : Noncototients". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
- "Sloane's A059756 : Erdős–Woods numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2020-12-04.
- "Sloane's A000045 : Fibonacci numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
- "Sloane's A002203 : Companion Pell numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
- Weisstein, Eric W. "Markov Number". mathworld.wolfram.com. Retrieved 2020-08-21.
- "Sloane's A000566 : Heptagonal numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-31.
- Sloane, N. J. A. (ed.). "Sequence A006003". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- "Counting polyhedra". Numericana. Retrieved 2022-04-20.
- Higgins, Peter (2008). Number Story: From Counting to Cryptography. New York: Copernicus. p. 53. ISBN 978-1-84800-000-1.
- "Evidence for a new nuclear 'magic number'" (Press release). Saitama, Japan: Riken. 2013-10-10. Retrieved 2013-10-14.
- Steppenbeck, D.; Takeuchi, S.; Aoi, N.; et al. (2013-10-10). "Evidence for a new nuclear 'magic number' from the level structure of 54Ca". Nature. 502 (7470): 207–210. Bibcode:2013Natur.502..207S. doi:10.1038/nature12522. PMID 24108051. S2CID 205235415.
- Jason M. Highsmith, MD (2020-03-03). "Spinal Anatomy Center". SpineUniverse. Retrieved 2022-08-10.
External links
- Prime Curios! 34 from the Prime Pages