Truncated tetraoctagonal tiling

In geometry, the truncated tetraoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,4}.

Truncated tetraoctagonal tiling
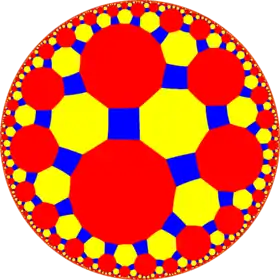Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.8.16
Schläfli symbol	tr{8,4} or $t{\begin{Bmatrix}8\\4\end{Bmatrix}}$
Wythoff symbol	2 8 4 \|
Coxeter diagram	or
Symmetry group	[8,4], (*842)
Dual	Order-4-8 kisrhombille tiling
Properties	Vertex-transitive

Dual tiling


The dual tiling is called an order-4-8 kisrhombille tiling, made as a complete bisection of the order-4 octagonal tiling, here with triangles are shown with alternating colors. This tiling represents the fundamental triangular domains of [8,4] (*842) symmetry.

Symmetry

Truncated tetraoctagonal tiling with *842,

, mirror lines

There are 15 subgroups constructed from [8,4] by mirror removal and alternation. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The subgroup index-8 group, [1⁺,8,1⁺,4,1⁺] (4242) is the commutator subgroup of [8,4].

A larger subgroup is constructed as [8,4*], index 8, as [8,4⁺], (4*4) with gyration points removed, becomes (*4444) or (*4⁴), and another [8*,4], index 16 as [8⁺,4], (8*2) with gyration points removed as (*22222222) or (*2⁸). And their direct subgroups [8,4*]⁺, [8*,4]⁺, subgroup indices 16 and 32 respectively, can be given in orbifold notation as (4444) and (22222222).

Small index subgroups of [8,4] (*842)
Index	1	2			4
Diagram
Coxeter	[8,4] =	[1⁺,8,4] =	[8,4,1⁺] = =	[8,1⁺,4] =	[1⁺,8,4,1⁺] =	[8⁺,4⁺]
Orbifold	*842	*444	*882	*4222	*4242	42×
Semidirect subgroups
Diagram
Coxeter		[8,4⁺]	[8⁺,4]	[(8,4,2⁺)]	[8,1⁺,4,1⁺] = = = =	[1⁺,8,1⁺,4] = = = =
Orbifold		4*4	8*2	2*42	2*44	4*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[8,4]⁺ =	[8,4⁺]⁺ =	[8⁺,4]⁺ =	[8,1⁺,4]⁺ =	[8⁺,4⁺]⁺ = [1⁺,8,1⁺,4,1⁺] = = =
Orbifold	842	444	882	4222	4242
Radical subgroups
Index		8	16		32
Diagram
Coxeter		[8,4*] =	[8*,4]	[8,4*]⁺ =	[8*,4]⁺
Orbifold		*4444	*22222222	4444	22222222

Related polyhedra and tilings

From a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-4 octagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 7 forms with full [8,4] symmetry, and 7 with subsymmetry.

Uniform octagonal/square tilings
[8,4], (842) (with [8,8] (882), [(4,4,4)] (444) , [∞,4,∞] (4222) index 2 subsymmetries) (And [(∞,4,∞,4)] (*4242) index 4 subsymmetry)
= = =	=	= = =	=	= =	=

{8,4}	t{8,4}	r{8,4}	2t{8,4}=t{4,8}	2r{8,4}={4,8}	rr{8,4}	tr{8,4}
Uniform duals


V8⁴	V4.16.16	V(4.8)²	V8.8.8	V4⁸	V4.4.4.8	V4.8.16
Alternations
[1⁺,8,4] (*444)	[8⁺,4] (8*2)	[8,1⁺,4] (*4222)	[8,4⁺] (4*4)	[8,4,1⁺] (*882)	[(8,4,2⁺)] (2*42)	[8,4]⁺ (842)
=	=	=	=	=	=

h{8,4}	s{8,4}	hr{8,4}	s{4,8}	h{4,8}	hrr{8,4}	sr{8,4}
Alternation duals


V(4.4)⁴	V3.(3.8)²	V(4.4.4)²	V(3.4)³	V8⁸	V4.4⁴	V3.3.4.3.8

n42 symmetry mutation of omnitruncated tilings: 4.8.2n*
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
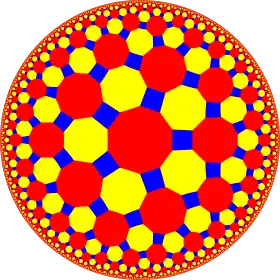
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	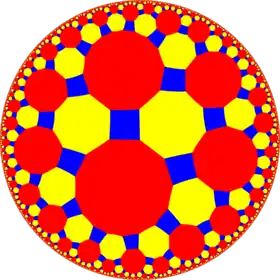4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n
Symmetry *nn2 [n,n]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *nn2 [n,n]	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Figure
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Dual
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

References

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.