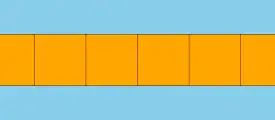
Apeirogonal prism
In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.[1]
| Apeirogonal prism | |
|---|---|
 | |
| Type | Semiregular tiling |
| Vertex configuration |  4.4.∞ |
| Schläfli symbol | t{2,∞} |
| Wythoff symbol | 2 ∞ | 2 |
| Coxeter diagram |     |
| Symmetry | [∞,2], (*∞22) |
| Rotation symmetry | [∞,2]+, (∞22) |
| Bowers acronym | Azip |
| Dual | Apeirogonal bipyramid |
| Properties | Vertex-transitive |
Thorold Gosset called it a 2-dimensional semi-check, like a single row of a checkerboard.
If the sides are squares, it is a uniform tiling. If colored with two sets of alternating squares it is still uniform.
Uniform variant with alternate colored square faces.
Its dual tiling is an apeirogonal bipyramid.
Related tilings and polyhedra
The apeirogonal tiling is the arithmetic limit of the family of prisms t{2, p} or p.4.4, as p tends to infinity, thereby turning the prism into a Euclidean tiling.
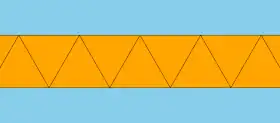
An alternation operation can create an apeirogonal antiprism composed of three triangles and one apeirogon at each vertex.
Similarly to the uniform polyhedra and the uniform tilings, eight uniform tilings may be based from the regular apeirogonal tiling. The rectified and cantellated forms are duplicated, and as two times infinity is also infinity, the truncated and omnitruncated forms are also duplicated, therefore reducing the number of unique forms to four: the apeirogonal tiling, the apeirogonal hosohedron, the apeirogonal prism, and the apeirogonal antiprism.
| (∞ 2 2) | Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|
| Wythoff symbol | 2 | ∞ 2 | 2 2 | ∞ | 2 | ∞ 2 | 2 ∞ | 2 | ∞ | 2 2 | ∞ 2 | 2 | ∞ 2 2 | | | ∞ 2 2 |
| Schläfli symbol | {∞,2} | t{∞,2} | r{∞,2} | t{2,∞} | {2,∞} | rr{∞,2} | tr{∞,2} | sr{∞,2} |
| Coxeter-Dynkin diagram |  |
|
|
|
|
|
|
 |
| Vertex config. | ∞.∞ | ∞.∞ | ∞.∞ | 4.4.∞ | 2∞ | 4.4.∞ | 4.4.∞ | 3.3.3.∞ |
| Tiling image |  |
|
|
|
 |
|
|
 |
| Tiling name | Apeirogonal dihedron | Apeirogonal dihedron | Apeirogonal dihedron | Apeirogonal prism | Apeirogonal hosohedron | Apeirogonal prism | Apeirogonal prism | Apeirogonal antiprism |
Notes
- Conway (2008), p.263
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
