Conjugado isotómico

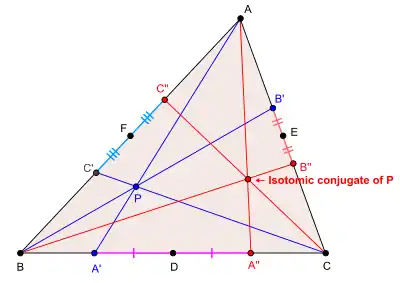
Supóngase que P no es colineal con dos vértices de ABC. Sean A', B' y C' los puntos en los que las líneas AP, BP y CP se cortan con los lados BC, CA y AB (extendidos si es necesario). Reflejando A', B', C' en los puntos medios de los lados BC, CA y AB, se obtienen respectivamente los puntos A", B" y C". Las tres líneas isotómicas AA", BB" y CC" que pasan por los vértices del triángulo se cortan en un punto, el conjugado isotómico de P (lo que puede ser probado usando el teorema de Ceva).

Si las coordenadas trilineales para P son p: q: r, entonces las trilineales para el conjugado isotómico de P son

a^-2p^-1: b^-2q^-1: c^-2r^-1,

donde a, b y c son las longitudes de los lados opuestos a los vértices A, B, y C respectivamente.

• El conjugado isotómico del centroide del triángulo ABC es el mismo centroide.

• El conjugado isotómico del punto simediano es el tercer punto de Brocard, y el conjugado isotómico del punto de Gergonne es el punto de Nagel.

• Los conjugados isotómicos de líneas rectas son circuncónicas, y por el contrario, los conjugados isotómicos de circuncónicas son rectas. Esta propiedad es válida también para los conjugados isogonales.

• Conjugado isogonal
• Elementos notables de un triángulo

• Robert Lachlan, An Elementary Treatise on Modern Pure Geometry, Macmillan and Co., 1893, page 57. ISBN 9781341105340

• Weisstein, Eric W. «Conjugado isotómico». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.