Dimensión
La dimensión (del latín dīmensiō, abstracto de dēmētiri, 'medir') es un número relacionado con las propiedades métricas o topológicas de un objeto matemático. La dimensión de un objeto es una medida topológica del tamaño de sus propiedades de recubrimiento. Existen diversas medidas o conceptualizaciones de dimensión: dimensión de un espacio vectorial, dimensión topológica, dimensión fractal, etcétera.[cita requerida]
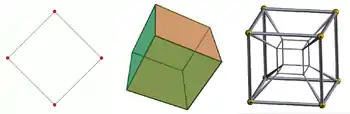
En geometría, en física y en ciencias aplicadas, la dimensión de un objeto se define informalmente como el número mínimo de coordenadas necesarias para especificar cualquier punto de ella.[1] Así, una línea tiene una dimensión porque solo se necesita una coordenada para especificar un punto de la misma. Una superficie, tal como un plano o la superficie de un cilindro o un circulo , tiene dos dimensiones, porque se necesitan dos coordenadas para especificar un punto en ella (por ejemplo, para localizar un punto en la superficie de una esfera se necesita su latitud y longitud). El interior de un cubo, de un cilindro o de una esfera es tridimensional porque son necesarias tres coordenadas para localizar un punto dentro de estos espacios. En casos más complicados como la dimensión fractal o la dimensión topológica de conjuntos abstractos, la noción de número [entero] de coordinadas no es aplicable y en esos casos deben usarse definiciones formales del concepto de dimensión.
También se usa el término "dimensión" para indicar el valor de una medida lineal o longitud recta de una figura geométrica u objeto físico, aunque dicho sentido no tiene relación con el concepto más abstracto de dimensión, que es el número de grados de libertad para realizar un movimiento en el espacio.
En mecánica clásica, el espacio y el tiempo son categorías diferentes y se refieren al espacio y tiempo absolutos. Esa concepción del mundo es un espacio cuatridimensional pero no el que se consideró necesario para describir el electromagnetismo. Las cuatro dimensiones (4D) del espaciotiempo consisten en sucesos que no están absolutamente definidos espacial y temporalmente, sino que se conocen en relación con el movimiento de un observador. El espacio de Minkowski es la primera aproximación al universo sin gravedad; las variedades pseudo-riemannianas de la relatividad general describen el espaciotiempo con materia y gravedad. Se utilizan 10 dimensiones para describir la teoría de supercuerdas (6D hiperespacio + 4D), 11 dimensiones pueden describir la supergravedad y la teoría M (7D hiperespacio + 4D), y el espacio de estados de la mecánica cuántica es un espacio de funciones infinito.
El concepto de dimensión no se limita a los objetos físicos. Los "espacios de alta dimensión" son frecuentes en las matemáticas y las ciencias. Pueden ser espacio euclidianos o espacio de parámetross más generales o espacios de configuración como en Lagrangiana o mecánica hamiltoniana; son espacios abstractos, independientes del espacio físico en el que vivimos.
Dimensiones físicas
El mundo físico en el que vivimos parece de cuatro dimensiones perceptibles. Tradicionalmente, se separa en tres dimensiones espaciales y una dimensión temporal (y en la mayoría de los casos es razonable y práctico). Podemos movernos hacia arriba o hacia abajo, hacia el norte o sur, este u oeste, y los movimientos en cualquier dirección pueden expresarse en términos de estos tres movimientos. Un movimiento hacia abajo es equivalente a un movimiento hacia arriba de forma negativa. Un movimiento norte-oeste es simplemente una combinación de un movimiento hacia el norte y de un movimiento hacia el oeste.
El tiempo, a menudo, es la cuarta dimensión. Es diferente de las tres dimensiones espaciales ya que solo hay uno, y el movimiento parece posible solo en una dirección. En el nivel macroscópico los procesos físicos no son simétricos con respecto al tiempo. Pero, a nivel subatómico (escala de Planck), casi todos los procesos físicos son simétricos respecto al tiempo (es decir, las ecuaciones utilizadas para describir estos procesos son las mismas independientemente de la dirección del tiempo), aunque esto no significa que las partículas subatómicas puedan regresar a lo largo del tiempo.
La Teoría de las cuerdas conjetura que el espacio en que vivimos tiene muchas más dimensiones (10, 11 o 26), pero que el universo medido a lo largo de estas dimensiones adicionales tienen tamaño subatómico. Estas ideas se basan en las ideas de los años 1920 en el contexto de las teorías de Kaluza-Klein.
En las ciencias físicas y la ingeniería, del tamaño de una magnitud física es la expresión del tipo de unidades de medida en que esta cantidad se expresa. La dimensión de la velocidad, por ejemplo, resulta de dividir la longitud entre el tiempo [L]/[T]. En el sistema SI, las dimensiones vienen dadas por 7 magnitudes fundamentales relacionadas con las características físicas fundamentales.
Dimensiones matemáticas
En matemáticas, no existe una definición de dimensión que incluya de manera adecuada todas las situaciones. En consecuencia, los matemáticos han elaborado muchas definiciones de dimensión para los diferentes tipos de espacio. Todas, sin embargo, están en última instancia, basadas en el concepto de la dimensión de un espacio euclídeo n, E n. El punto E 0 es 0-dimensional. La línea E 1 es 1-dimensional. El plano E 2 es 2-dimensional. En general, E n es n-dimensional.
Dimensión de un espacio vectorial
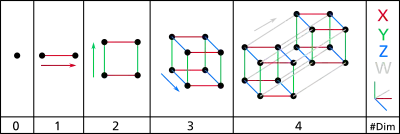
Un espacio vectorial sobre un cuerpo que se dice que tiene dimensión si existe una base de cardinal n. En un espacio vectorial, todas las bases tienen el mismo cardinal, lo que hace de la dimensión el primer invariante del álgebra lineal. El espacio vectorial trivial {0} tiene como dimensión 0 porque el conjunto vacío es su base: una combinación de cero vector da el vector nulo.
Intuitivamente hablando, la dimensión de un espacio vectorial nos dice cuántos elementos necesitamos para poder expresar cualquier elemento del espacio en términos de las combinaciones lineales de los primeros, i.e., cuántos elementos del espacio necesitamos para poder expresar todos los elementos del espacio como sumas de múltiplos de estos elementos. Los espacios vectoriales de dimensión finita son muy comunes en muchas áreas de la ciencia, pero en matemáticas y física cuántica también aparecen casos importantes de espacios vectoriales de dimensión infinita.
Dimensión topológica
La dimensión topológica es un número entero, definible para cualquier espacio topológico. Para un espacio formado por un punto la dimensión topológica es 0, para la recta real es 1, para el plano euclídeo es 2, etc.
Más formalmente escrito, un objeto tiene dimensión topológica m cuando cualquier recubrimiento de ese objeto, tiene como mínimo una dimensión topológica = m+1 (estableciendo previamente que el punto tiene dimensión topológica = 0).
Aún más formalmente: la definición para conjuntos con dimensión topológica 0 queda como sigue: se dice que un conjunto F tiene dimensión topológica 0, , si y solo si para todo x perteneciente a F y cualquier conjunto abierto U (para la topología relativa de F) que contenga a x, existe un abierto V tal que x pertenece a V que está incluido en U y la frontera de V con la intersección a F es vacía.
Dimensión fractal de Hausdorff-Besicovitch
Esta dimensión es comúnmente confundible con la entropía de Kolmogórov o la dimensión de Minkowski Bouligand. La dimensión de Hausdorff-Besicovitch se obtiene como un punto de inflexión del valor de la potencia elegida en la longitud de Hausdorff cuando esta pasa de ser infinita a ser nula. La longitud de Hausdorff es la suma del diámetro topológico elevado a una potencia "s" de un recubrimiento entero del objeto a partir de entornos o cubrimientos de diámetro delta o menor a este del propio objeto.
La entropía de Kolmogórov
Se denomina entropía de Kolmogórov a una dimensión obtenida para facilidad de cálculos como el cociente logarítmico entre el número de homotecias internas encontradas en un objeto por transformación, y la inversa de la razón de esa homotecia. Es también llamada dimensión por contaje de cajas y tiene una definición más intuitiva pero más larga al respecto.
Es de esta manera que los objetos euclidianos diferenciables se ven con una correspondencia en su valor dimensional topológica, dimensión de contaje de cajas y dimensión de Hausdorff-Besicovitch. Esto no resulta con los fractales, donde son definidos por Benoit Mandelbrot como:
Objetos tales que su dimensión de Hausdorff - Besicovitch excede estrictamente su dimensión topológica.
Finalmente sabemos que existen casos de fractales que no se apegan a esta definición; una de esas es la curva del Diablo, la cual es un fractal derivado del conjunto de Cantor.
En física
Dimensiones espaciales
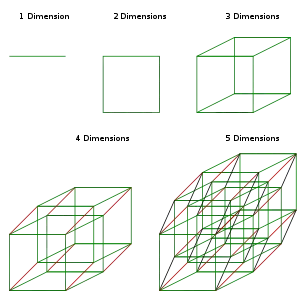
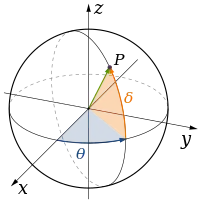
Las teorías físicas clásicas describen tres dimensiones físicas: desde un punto concreto del espacio, las direcciones básicas en las que podemos movernos son arriba/abajo, izquierda/derecha y adelante/atrás. El movimiento en cualquier otra dirección puede expresarse en términos de estas tres direcciones. Moverse hacia abajo es lo mismo que moverse hacia arriba una distancia negativa. Moverse diagonalmente hacia arriba y hacia adelante es tal como el nombre de la dirección implica; es decir, moverse en una combinación lineal de arriba y adelante. En su forma más simple: una línea describe una dimensión, un plano describe dos dimensiones y un cubo describe tres dimensiones. (Véanse Espacio y Sistema de coordenadas cartesianas).
| Número de dimensiones |
Ejemplos de sistemas de coordenadas | |||
|---|---|---|---|---|
| 1 |
| |||
| 2 |
| |||
| 3 |
|
Tiempo
Una dimensión temporal, o dimensión temporal, es una dimensión del tiempo. A menudo se hace referencia al tiempo como la cuarta dimensión del espaciotiempo por esta razón, pero esto no implica que sea una dimensión espacial. La dimensión temporal es una forma de medir el cambio físico. Se percibe de forma diferente a las tres dimensiones espaciales en el sentido de que sólo hay una y que no podemos movernos libremente en el tiempo, sino que nos movemos subjetivamente en una dirección.
Las ecuaciones utilizadas en física para modelar la realidad no tratan el tiempo de la misma manera que los humanos lo perciben comúnmente. Las ecuaciones de la mecánica clásica son simétricas con respecto al tiempo, y las ecuaciones de la mecánica cuántica son típicamente simétricas si tanto el tiempo como otras cantidades (como la carga y la paridad) se invierten. En estos modelos, la percepción de que el tiempo fluye en una dirección es un artefacto de las leyes de la termodinámica (percibimos que el tiempo fluye en la dirección del aumento de la entropía). Según Ouspensky, la cuarta dimensión, a la que tan difícil le es acceder al ser humano, es la dimensión del tiempo. El tiempo es la categoría a la cual nos resulta tan complicado acceder y la dimensión siguiente a la que deberíamos trascender, se respondió a sí mismo Ouspensky en sus fascinantes investigaciones. Según él,el tiempo es la cuarta dimensión que sería circular. Por ello la sensación cíclica de que todo se repite, no sólo en la vida del ser humano sino también en la historia humana, biológica, en la de los planetas, el Sol y el universo en general. Ouspensky comprendió de esta manera el carácter circular del tiempo y de la cuarta dimensión
El tratamiento más conocido del tiempo como una dimensión es la relatividad especial de Poincaré y Einstein (y extendida a la relatividad general), que trata el espacio y el tiempo percibidos como componentes de un múltiple de cuatro dimensiones, conocido como espaciotiempo, y en el caso especial y plano como espacio de Minkowski. El tiempo es diferente de otras dimensiones espaciales, ya que el tiempo opera en todas las dimensiones espaciales. El tiempo opera en la primera, segunda y tercera dimensiones espaciales, así como en dimensiones espaciales teóricas como una cuarta dimensión espacial. Sin embargo, el tiempo no está presente en un único punto de singularidad infinita absoluta, definido como un punto geométrico, ya que un punto infinitamente pequeño no puede tener ningún cambio y, por tanto, ningún tiempo. Al igual que cuando un objeto se mueve a través de posiciones en el espacio, también se mueve a través de posiciones en el tiempo. En este sentido la fuerza que mueve a cualquier objeto a cambiar es el tiempo.[2][3][4]
En ciencia ficción
En ciencia ficción, a veces se usa el término "dimensión" como sinónimo de universo paralelo; aunque el término esté relacionado no son sinónimos (véase teoría de las cuerdas).
Véase también
Referencias
- MathWorld: Dimension
- Rylov, Yuri A. (2007). «Método no euclidiano de la construcción geométrica generalizada y su aplicación a la geometría espacio-temporal». .
- Lane, Paul M.; Lindquist, Jay D. (22 de mayo de 2015). «Definiciones para La Cuarta Dimensión: A Proposed Time Classification System1». En Bahn, Kenneth D., ed. Proceedings of the 1988 Academy of Marketing Science (AMS) Annual Conference. Developments in Marketing Science: Proceedings of the Academy of Marketing Science. Springer International Publishing. pp. 38-46. ISBN 978-3-319-17045-9. doi:10.1007/978-3-319-17046-6_8 – via Springer Link.
- Wilson, Edwin B.; Lewis, Gilbert N. (1912). «El Manifold Espacio-Tiempo de la Relatividad. The Non-Euclidean Geometry of Mechanics and Electromagnetics». Proceedings of the American Academy of Arts and Sciences 48 (11): 389-507. JSTOR 20022840. doi:10.2307/20022840 – via JSTOR.
Bibliografía
- Murty, Katta G. (2014). «1. Systems of Simultaneous Linear Equations». Computational and Algorithmic Linear Algebra and n-Dimensional Geometry. World Scientific Publishing. ISBN 978-981-4366-62-5. doi:10.1142/8261.
- Abbott, Edwin A. (1884). Flatland: A Romance of Many Dimensions. London: Seely & Co.
- —. Flatland: .... Project Gutenberg.
- —; Stewart, Ian (2008). The Annotated Flatland: A Romance of Many Dimensions. Basic Books. ISBN 978-0-7867-2183-2.
- Banchoff, Thomas F. (1996). Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions. Scientific American Library. ISBN 978-0-7167-6015-3.
- Pickover, Clifford A. (2001). Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons. Oxford University Press. ISBN 978-0-19-992381-6.
- Rucker, Rudy (2014). The Fourth Dimension: Toward a Geometry of Higher Reality. Courier Corporation. ISBN 978-0-486-77978-2. Google preview
- Kaku, Michio (1994). Hyperspace, a Scientific Odyssey Through the 10th Dimension. Oxford University Press. ISBN 978-0-19-286189-4.
- Krauss, Lawrence M. (2005). Hiding in the Mirror. Viking Press. ISBN 978-0-670-03395-9.

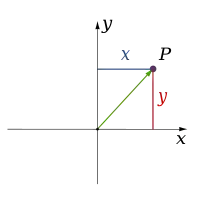

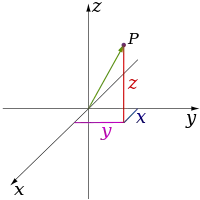

.svg.png.webp)