Ecuación podal
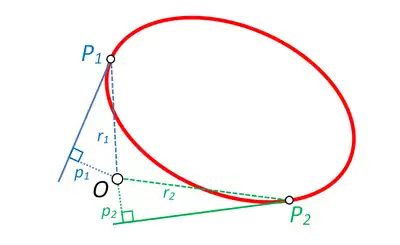
Para un curva plana C y un punto fijo dado O, la ecuación podal de la curva es una relación entre r y p, donde r es la distancia desde O a un punto en C y p es la distancia perpendicular desde O a la tangente a C en el punto considerado. El punto O se llama punto podal y los valores r y p se llaman coordenadas podales de un punto relativo a la curva y al punto podal. También es útil medir la distancia de O a la normal (la coordenada contrapodal) aunque no es una cantidad independiente y se relaciona con como .
Algunas curvas tienen ecuaciones podales particularmente simples, por lo que pueden simplificar el cálculo de algunas de sus propiedades, como la curvatura. Estas coordenadas también son adecuadas para resolver ciertos tipos de problemas de fuerza en mecánica clásica y mecánica celeste.
Ecuaciones
Coordenadas cartesianas
Para C dada en coordenadas cartesianas por f (x, y) = 0, y con O tomado como origen, las coordenadas podales del punto (x, y) están dadas por:[1]
La ecuación podal se puede encontrar eliminando x e y de estas ecuaciones y de la ecuación de la curva.
La expresión para p se puede simplificar si la ecuación de la curva se escribe en coordenadas homogéneas introduciendo una variable z, de modo que la ecuación de la curva sea g (x, y, z) = 0. El valor de p viene dado por[2]
donde el resultado se obtiene para z = 1
Coordenadas polares
Para C dada en coordenadas polares por r = f(θ), entonces
donde ψ es el ángulo tangencial polar dado por
La ecuación podal se puede deducir eliminando θ de estas ecuaciones.[3]
Alternativamente, de lo anterior, se tiene que
donde es la coordenada "contrapodal", es decir, la distancia a la normal. Esto implica que si una curva satisface una ecuación diferencial autónoma en coordenadas polares de la forma:
su ecuación de podal se convierte en
Ejemplo
Como ejemplo, tómese la espiral logarítmica con el ángulo en espiral α:
Diferenciando con respecto a se obtiene
por lo tanto
y así en coordenadas podales resulta
o utilizando el hecho de que se obtiene
Este enfoque puede generalizarse para incluir ecuaciones diferenciales autónomas de cualquier orden de la siguiente manera:[4] Una curva C, solución de una n-ésima ecuación diferencial autónoma () en coordenadas polares
es la podaria de una curva dada en coordenadas de podales por
donde la diferenciación se hace con respecto a .
Problemas de fuerzas
Las soluciones a algunos problemas de fuerzas de la mecánica clásica se pueden obtener de manera sorprendentemente fácil en coordenadas de podales.
Considérese un sistema dinámico:
describiendo la evolución de una partícula de prueba (con posición y velocidad ) en el plano en presencia de una fuerza central y potencial de Lorentz . Las cantidades:
se conservan en este sistema.
A continuación, la curva trazada por se da en coordenadas podales por
con el punto podal en el origen. Este hecho fue descubierto por P. Blaschke en 2017.[5]
Ejemplo
Como ejemplo, considérese el llamado problema de Kepler, es decir, el caso de una fuerza central, que varía inversamente con el cuadrado de la distancia:
Se puede llegar a la solución de inmediato en coordenadas podales
- ,
donde corresponde al momento angular de la partícula y a su energía. Por lo tanto, se ha obtenido la ecuación de una sección cónica en coordenadas podales.
Inversamente, para una curva dada C, se puede deducir fácilmente qué fuerzas hay que imponer sobre una partícula de prueba para moverse sobre ella.
Ecuaciones podales para curvas específicas
Espirales sinusoidales
Para una espiral sinusoidal descrita según la fórmula
el ángulo tangencial polar es
que produce la ecuación podal
La ecuación podal para un numerosas curvas conocidas se puede obtener dando a n valores específicos:[6]
| n | Curva | Punto podal | Ecuación podal |
|---|---|---|---|
| 1 | Circunferencia de radio a | Punto en la circunferencia | pa = r2 |
| −1 | Recta | Punto a una distancia a de la recta | p = a |
| 1⁄2 | Cardioide | Cúspude | p2a = r3 |
| −1⁄2 | Parábola | Foco | p2 = ar |
| 2 | Lemniscata de Bernoulli | Centro | pa2 = r3 |
| −2 | Hipérbola | Centro | rp = a2 |
Espirales
Una curva espiral de la forma
satisface la ecuación
y así se puede convertir fácilmente en coordenadas podales como
Los casos especiales incluyen:
| Curva | Punto podal | Ecuación podal | |
|---|---|---|---|
| 1 | Espiral de Arquímedes | Origen | |
| −1 | Espiral hiperbólica | Origen | |
| 1⁄2 | Espiral de Fermat | Origin | |
| −1⁄2 | Lituus | Origen |
Epicicloides e hipocicloides
Para una epi o hipocicloide dada por ecuaciones paramétricas
la ecuación podal con respecto al origen es [7]
o[8]
con
Los casos especiales que se obtienen al establecer b = a⁄n para valores específicos de n incluyen:
| n | Curva | Ecuación podal |
|---|---|---|
| 1, −1⁄2 | Cardioide | |
| 2, −2⁄3 | Nefroide | |
| −3, −3⁄2 | Deltoide | |
| −4, −4⁄3 | Astroide |
Otras curvas
Otras ecuaciones podales son:[9]
| Curva | Ecuación | Punto podal | Ecuación podal |
|---|---|---|---|
| Recta | Origen | ||
| Punto | Origen | ||
| Circunferencia | Origen | ||
| Involuta de una circunferencia | Origen | ||
| Elipse | Centro | ||
| Hipérbola | Centro | ||
| Elipse | Foco | ||
| Hipérbola | Foco | ||
| Espiral logarítmica | Polo | ||
| Óvalo cartesiano | Foco | ||
| Óvalo de Cassini | Foco | ||
| Óvalo de Cassini | Centro |
Véase también
Referencias
- Yates §1
- Edwards p. 161
- Yates p. 166, Edwards p. 162
- Blaschke Proposition 1
- Blaschke Theorem 2
- Yates p. 168, Edwards p. 162
- Edwards p. 163
- Yates p. 163
- Yates p. 169, Edwards p. 163, Blaschke sec. 2.1
Bibliografía
- R.C. Yates (1952). «Pedal Equations». A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 166 ff.
- J. Edwards (1892). Differential Calculus. London: MacMillan and Co. pp. 161 ff.
- P. Blaschke (2017). «Pedal coordinates, dark Kepler and other force problems». Journal of Mathematical Physics. 58/6. doi:10.1063/1.4984905.
Enlaces externos
- Weisstein, Eric W. «Pedal coordinates». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.