Hemipoliedro

Sus símbolos de Wythoff tienen la forma ^p/_(p − q) ^p/_q | r; y sus figuras de vértice son cuadriláteros cruzados. Por lo tanto, están relacionados con los poliedros canteados, que tienen símbolos de Wythoff similares. La configuración de vértices es ^p/_q.2r. ^p/_(p − q).2r. Las caras de 2r-gónicas pasan por el centro del modelo: si se representan como caras de un poliedro esférico, cubren un hemisferio completo y sus aristas y vértices se encuentran en un círculo máximo. La notación ^p/_(p − q) implica una cara {^p/_q} que gira hacia atrás alrededor de la figura de vértice.

Las nueve formas, enumeradas con sus símbolos de Wythoff y configuraciones de vértices son:

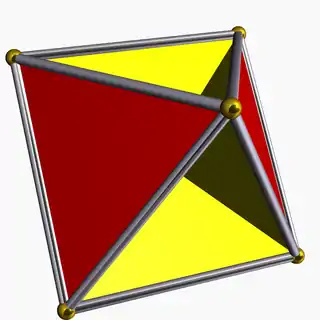Tetrahemihexaedro 3/2 3 | 2 (3.4.3/2.4) (p/q = 3, r = 2)	Octahemioctaedro 3/2 3 | 3 (3.6.3/2.6) (p/q = 3, r = 3)	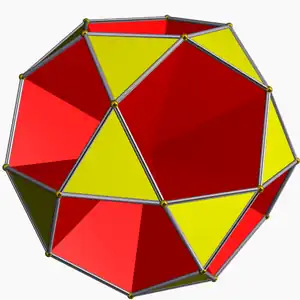Pequeño icosihemidodecaedro 3/2 3 | 5 (3.10.3/2.10) (p/q = 3, r = 5)	Gran icosihemidodecaedro 3/2 3 | 5/3 (3.10/3.3/2.10/3) (p/q = 3, r = 5/3)	Pequeño dodecahemicosaedro 5/3 5/2 | 3 (5/2.6.5/3.6) (p/q = 5/2, r = 3)
	Cubohemioctaedro 4/3 4 | 3 (4.6.4/3.6) (p/q = 4, r = 3)	Pequeño dodecahemidodecaedro 5/4 5 | 5 (5.10.5/4.10) (p/q = 5, r = 5)	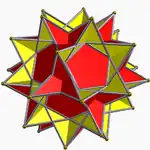Gran dodecahemidodecaedro 5/3 5/2 | 5/3 (5/2.10/3.5/3.10/3) (p/q = 5/2, r = 5/3)	Gran dodecahemicosaedro 5/4 5 | 3 (5.6.5/4.6) (p/q = 5, r = 3)

Debe tenerse en cuenta que la construcción caleidoscópica de Wythoff genera los hemipoliedros no orientables (todos excepto el octahemioctaedro) como recubrimientos dobles (dos hemipoliedros coincidentes).

En el plano euclídeo, la secuencia de hemipoliedros continúa con las siguientes cuatro teselaciones estrelladas, donde los apeirógonos aparecen como los polígonos ecuatoriales antes mencionados:

Teselado rectificado original	Diagrama de aristas	Sólido	Configuración de vértices	Wythoff	Simetría
Teselado cuadrado			4.∞.4/3.∞ 4.∞.-4.∞	∞	p4m
Teselado triangular			(3.∞.3.∞.3.∞)/2	3 ∞	p6m
Teselado trihexagonal			6.∞.6/5.∞ 6.∞.-6.∞	∞
			∞.3.∞.3/2 ∞.3.∞.-3	∞

De estos cuatro teselados, solo el 6/5 6 | ∞ se genera como un doble recubrimiento según la construcción de Wythoff.

Solo el octahemioctaedro representa una superficie orientable; los hemipoliedros restantes tienen superficies no orientables o de un solo lado. Esto se debe a que al proceder alrededor de un 2r-gono ecuatorial, las caras ^p/_q-gonales apuntan alternativamente "arriba" y "abajo", por lo que dos consecutivas tienen sentidos opuestos. Esto es equivalente a exigir que los ^p/_q-gons en los poliedros cuasiregulares correspondientes que figuran a continuación puedan tener orientaciones positivas y negativas alternativamente. Pero eso solo es posible para los triángulos del cuboctaedro (correspondientes a los triángulos del octaedro, el único poliedro regular con un número "par" de caras que se unen en un vértice), que son precisamente las caras que no son hemicaras del octahemioctaedro.[2]

Dado que los hemipoliedros tienen caras pasando por su centro, sus figuras duales tienen vértices correspondiente en el infinito del plano proyectivo real.[3] En los "Modelos duales" de Magnus Wenninger, se representan con prismas intersecados, cada uno de los cuales se extiende en ambas direcciones hasta el mismo vértice en el infinito para mantener la simetría. En la práctica, los prismas del modelo se cortan en un punto determinado conveniente para facilitar su representación. Wenninger sugirió que estas figuras son miembros de una nueva clase de figuras de estelación, denominadas "estelación hasta el infinito". Sin embargo, también sugirió que estrictamente hablando no son poliedros porque su construcción no se ajusta a las definiciones habituales.

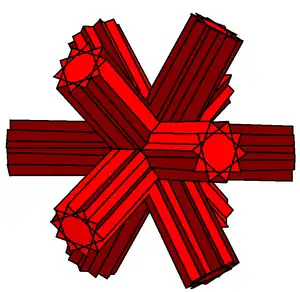
Existen 9 poliedros duales de este tipo, que comparten solo 5 formas externas distintas, cuatro de las cuales existen en pares aparentemente idénticos. Los miembros de un par dado visualmente idéntico difieren en la disposición de los vértices verdaderos y los falsos (un vértice falso es aquel en que dos aristas se cruzan pero no se unen). Las formas exteriores son:

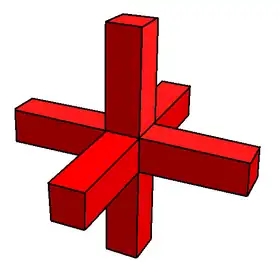Tetrahemihexaedro	Octahemioctaedro y cubohemioctaedro	Pequeño icosihemidodecacrón y pequeño dodecahemidodecacrón	Gran dodecahemidodecacrón y gran icosihemidodecacrón	Gran dodecahemicosacrón y pequeño dodecahemicosacrón
3 cuboides infinitos que se intersecan	4 prismas hexagonales infinitos que se intersecan	6 prismas decagonales infinitos que se intersecan	6 prismas decagrámicos infinitos que se intersecan	10 prismas hexagonales infinitos que se intersecan

Los hemipoliedros aparecen en pares como facetados de poliedros cuasirregulares con cuatro caras en un vértice. Estos poliedros cuasiregulares tienen configuraciones de vértice m.n.m.n y sus aristas, además de formar la m- y n -caras agonales, también forman las hemicaras de los hemipoliedros. Por lo tanto, los hemipoliedros se pueden obtener de los poliedros cuasirregulares descartando los "m"-gonos o "n"-gonos (para mantener dos caras en cada arista) y luego insertando las hemicaras. Dado que se pueden descartar m-gonos o n-gonos, cualquiera de los dos hemipoliedros pueden obtenerse a partir de cada poliedro cuasiregular, excepto el octaedro como tetratetraedro, donde m = n = 3 y las dos caras son congruentes (esta construcción no funciona para los poliedros cuasiregulares con seis caras en un vértice, también conocidos como poliedros ditrigonales, ya que sus aristas no forman hemicaras regulares).[1]

Dado que los hemipoliedros, al igual que los poliedros cuasirregulares, también tienen dos tipos de caras que se alternan alrededor de cada vértice, a veces también se los considera cuasirregulares.[1]

Poliedro cuasirregular m.n.m.n	Hemicaras (h-gonos)	Hemipoliedro con m-gonos sin caras redundantes n.h.n/n - 1.h	Hemipoliedro con n-gonos sin caras redundantes m.h.m/m - 1.h
Octaedro 3.3.3.3 m= 3, n= 3	Cuadrados {4}	Tetrahemihexaedro 3.4.3/2.4	Tetrahemihexaedro 3.4.3/2.4
Cuboctaedro 3.4.3.4 m= 3, n= 4	Hexágonos {6}	Cubohemioctaedro 4.6.4/3.6	Octahemioctaedro 3.6.3/2.6
Icosidodecaedro 3.5.3.5 m= 3, n= 5	decágonos {10}	Pequeño dodecahemidodecaedro 5.10.5/4.10	Pequeño icosihemidodecaedro 3.10.3/2.10
Dodecadodecaedro 5.5/2.5.5/2 m= 5, n= 5/2	hexágonos {6}	Pequeño dodecahemicosaedro 5/2.6.5/3.6	Gran dodecahemicosaedro 5.6.5/4.6
Gran icosidodecaedro 3.5/2.3.5/2 m= 3, n= 5/2	Decagramas {10/3}	Gran dodecahemidodecaedro 5/2.10/3.5/3.10/3	Gran icosihemidodecaedro 3.10/3.3/2.10/3

Aquí m y n corresponden a ^p/_q en párrafos anteriores, y h corresponde a 2r.

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), «Uniform polyhedra», Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 401-450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003.
• Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493. (modelos Wenninger: 67, 68, 78, 89, 91, 100, 102, 106, 107)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208.
• Har'El, Z. Solución uniforme para poliedros uniformes., Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El (Página 10, 5.2. Hemi poliedros p p'|r.)

• Glosario poliédrico de Stella
• Versi-poliedros regulares en poliedros visuales