The fifty nine icosahedra
The Fifty-Nine Icosahedra (Los Cincuenta y Nueve Icosaedros) es un libro escrito e ilustrado por H. S. M. Coxeter, P. Du Val, H. T. Flather y J. F. Petrie. Enumera ciertas estelaciones del icosaedro regular convexo o platónico, de acuerdo con un conjunto de reglas propuestas por J. C. P. Miller.

Publicado por primera vez por la Universidad de Toronto en 1938, Springer-Verlag reeditó el libro en 1982. La tercera edición de Tarquin de 1999 incluyó nuevo material de referencia y fotografías de K. y D. Crennell.
Contribuciones de los autores
Reglas de Miller
Aunque Miller no contribuyó directamente al libro, fue un colega cercano de Coxeter y Petrie. Su aportación está inmortalizada en su conjunto de reglas para definir qué formas de estelación deben considerarse "adecuadamente significativas y distintas":[1]
- (i) Las caras deben estar en veinte planos, a saber, los planos delimitadores del icosaedro regular.
- (ii) Todas las partes que componen las caras deben ser iguales en cada plano, aunque pueden estar desconectadas entre sí.
- (iii) Las partes incluidas en cualquier plano deben tener simetría trigonal, con o sin reflexión. Esto asegura la simetría icosaédrica para todo el sólido.
- (iv) Las partes incluidas en cualquier plano deben ser todas "accesibles" en el sólido completo (es decir, deben estar en el "exterior". En ciertos casos deberíamos requerir modelos de enorme tamaño para poder ver todo el exterior. Con un modelo de tamaño ordinario, algunas partes del "exterior" solo podrían ser exploradas por un diminuto insecto).
- (v) Excluimos de la consideración los casos en que las partes se pueden dividir en dos conjuntos, cada uno de los cuales da un sólido con tanta simetría como la figura completa. Pero permitimos la combinación de un par enantiomorfo que no tiene una parte común (lo que en realidad ocurre en un solo caso).
Las reglas (i) a (iii) son requisitos de simetría para los planos frontales. La regla (iv) excluye los agujeros enterrados, para garantizar que no haya dos estelaciones aparentemente idénticas. La regla (v) evita cualquier compuesto desconectado de estelaciones más simples.
Coxeter
Coxeter fue la principal fuerza impulsora detrás del trabajo. Llevó a cabo el análisis original basado en las reglas de Miller, adoptando una serie de técnicas como la combinatoria y la teoría de grafos abstracta, cuyo uso en un contexto geométrico era entonces novedoso.
Observó que el diagrama de la estelación constaba de muchos segmentos de línea. Luego desarrolló procedimientos para manipular combinaciones de las regiones planas adyacentes, con el fin de enumerar formalmente las combinaciones permitidas por las reglas de Miller.
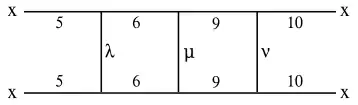
Su gráfico, reproducido aquí, muestra la conectividad de las diversas caras identificadas en el diagrama de la estelación (véase más abajo). Los símbolos griegos representan conjuntos de posibles alternativas:
- λ puede ser 3 o 4
- μ puede ser 7 u 8
- ν puede ser 11 o 12
Du Val
Du Val ideó una notación simbólica para identificar conjuntos de celdas congruentes, basándose en la observación de que se encuentran formando cáscaras alrededor del icosaedro original. Basándose en esto, probó todas las combinaciones posibles sobre las reglas de Miller, confirmando el resultado del enfoque más analítico de Coxeter.
Flather
La contribución de Flather fue indirecta, realizando modelos en cartulina de los 59 casos. Cuando conoció a Coxeter, ya había confeccionado numerosas estelaciones, incluidos algunos ejemplos que no cumplían las reglas de Miller. Luego pasó a completar la serie de cincuenta y nueve modelos, que se conservan en la biblioteca de matemáticas de la Universidad de Cambridge, Inglaterra. La biblioteca también tiene algunos modelos que no cumplen las reglas de Miller, pero no se sabe si fueron realizados por Flather o por los estudiantes posteriores de Miller.[2]
Petrie
John Flinders Petrie fue amigo de toda la vida de Coxeter y tenía una notable habilidad para visualizar la geometría en cuatro dimensiones. Junto con Coxeter, había trabajado en muchos problemas matemáticos. Su contribución directa a los cincuenta y nueve icosaedros fue el exquisito conjunto de dibujos tridimensionales que proporcionan gran parte del fascinante aspecto de la obra publicada.
Los Crennell
Para la Tercera Edición, Kate y David Crennell reajustaron el texto y redibujaron los diagramas. También agregaron una sección de referencia que contenía tablas, diagramas y fotografías de algunos de los modelos de Cambridge (que en ese momento se pensaba que eran todos de Flather). Las correcciones a esta edición se han publicado en línea.[3]
Lista de los cincuenta y nueve icosaedros
Antes de Coxeter, solo Brückner y Wheeler habían registrado conjuntos significativos de estelaciones, aunque algunas, como el gran icosaedro, se conocían desde hacía más tiempo. Desde la edición de The 59, Wenninger publicó instrucciones sobre cómo realizar modelos de algunas estelaciones. El esquema de numeración utilizado en su libro se ha vuelto ampliamente referenciado, aunque solo registró algunas de estas estelaciones.
Notas sobre la lista
Los números de índice son los de Crennell a menos que se indique lo contrario:
Crennell
- En la numeración del índice agregada a la Tercera Edición por los Crennell, las primeras 32 formas (índices 1-32) son modelos reflejados, y las últimas 27 (índices 33–59) son quirales y solo se enumeran las formas dextrógiras. Este es el orden en que se representan las estelaciones en el libro.
Celdas
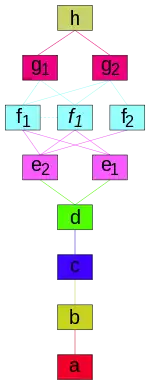
- En la notación de Du Val, cada capa se identifica en negrita, trabajando hacia afuera, como a, b, c, ..., h, siendo a el icosaedro original. Algunas capas se subdividen en dos tipos de celdas, por ejemplo e comprende e1 y e2. El conjunto f1 se subdivide en formas a derecha e izquierda, respectivamente f1 (letra normal) y f1 (letra cursiva). Cuando una estelación tiene todas las celdas presentes dentro de una capa exterior, la capa exterior se escribe con mayúscula y la interior se omite, por ejemplo a + b + c + e1 se escribe como Ce1.
Caras
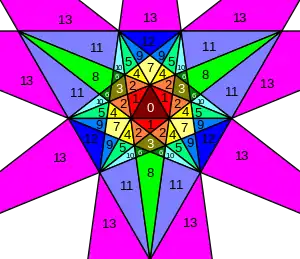
- Todas las estelaciones se pueden especificar mediante un diagrama de estelación. En el diagrama que se muestra aquí, los colores numerados indican las regiones del diagrama de estelación que deben aparecer juntas como un conjunto, si se quiere mantener la simetría icosaédrica completa. El diagrama tiene 13 conjuntos de este tipo. Algunos de estos se subdividen en pares quirales (no mostrados), lo que permite estelaciones con simetría rotacional pero no reflexiva. En la tabla, las caras que se ven desde abajo se indican con un apóstrofe, por ejemplo 3'.
Wenninger
- Los números de índice y los nombres numerados fueron asignados arbitrariamente por el editor de Wenninger de acuerdo con su aparición en su libro "Modelos de poliedros" y no guardan relación con ninguna secuencia matemática. Solo algunos de sus modelos eran de icosaedros. Sus nombres se dan en forma abreviada, dejando "... del icosaedro".
Wheeler
- Wheeler encontró sus figuras, o formas del icosaedro, seleccionando segmentos de línea del diagrama de la estelación. Distinguió cuidadosamente esto del proceso clásico de estelación ideado por Johannes Kepler. Coxeter et al. ignoró esta distinción y se refirió a todos ellos como estelaciones.
Brückner
- Max Brückner hizo y fotografió modelos de muchos poliedros, de los cuales solo unos pocos eran icosaedros. Taf. es una abreviatura de Tafel, palabra que en alemán da nombre a una imagen impresa mediante fototipia.
Observaciones
- La figura No. 8 a veces se llama el equidnaedro debido a su relativa similitud con un equidna. Este uso es independiente de la descripción que hace Johannes Kepler de un poliedro regular estrellado al que denominó equidnae.
Tabla de los cincuenta y nueve icosaedros
Algunas imágenes ilustran el icosaedro de imagen especular con la celda f1 en lugar de con la celda f1.
| Crennell | Celdas | Caras | Wenninger | Wheeler | Brückner | Observaciones | Diagrama de caras | 3D |
|---|---|---|---|---|---|---|---|---|
| 1 | A | 0 | 4 Icosaedro | 1 | El icosaedro platónico |  |
 | |
| 2 | B | 1 | 26 Triaquisicosaedro |
2 | Taf. VIII, Fig. 2 | Primera estelación del icosaedro, pequeño icosaedro triámbico, o triaquisicosaedro |
 |
 |
| 3 | C | 2 | 23 Compuesto de cinco octaedros | 3 | Taf. IX, Fig. 6 | Compuesto de cinco octaedros regular |  |
 |
| 4 | D | 3 4 | 4 | Taf. IX, Fig.17 |  |
 | ||
| 5 | E | 5 6 7 | 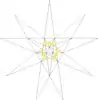 |
 | ||||
| 6 | F | 8 9 10 | 27 Segunda estelación | 19 | Segunda estelación del icosaedro |  |
 | |
| 7 | G | 11 12 | 41 Gran icosaedro | 11 | Taf. XI, Fig. 24 | Gran icosaedro |  |
 |
| 8 | H | 13 | 42 Estelación final | 12 | Taf. XI, Fig. 14 | Estelación final del icosaedro o equidnaedro |  |
 |
| 9 | e1 | 3' 5 | 37 Duodécima estelación | Duodécima estelación del icosaedro |  |
 | ||
| 10 | f1 | 5' 6' 9 10 | 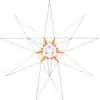 |
 | ||||
| 11 | g1 | 10' 12 | 29 Cuarta estelación | 21 | Cuarta estelación del icosaedro |  |
 | |
| 12 | e1f1 | 3' 6' 9 10 | 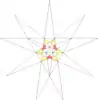 |  | ||||
| 13 | e1f1g1 | 3' 6' 9 12 | 20 |  |
 | |||
| 14 | f1g1 | 5' 6' 9 12 | 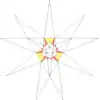 |  | ||||
| 15 | e2 | 4' 6 7 | 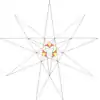 |  | ||||
| 16 | f2 | 7' 8 | 22 | 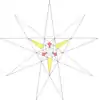 |
 | |||
| 17 | g2 | 8' 9'11 |  |  | ||||
| 18 | e2f2 | 4' 6 8 | 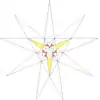 |  | ||||
| 19 | e2f2g2 | 4' 6 9' 11 | 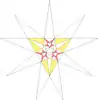 |  | ||||
| 20 | f2g2 | 7' 9' 11 | 30 Quinta estelación | Quinta estelación del icosaedro |  |
 | ||
| 21 | De1 | 4 5 | 32 Séptima estelación | 10 | Séptima estelación del icosaedro |  |
 | |
| 22 | Ef1 | 7 9 10 | 25 Compuesto de diez tetraedros | 8 | Taf. IX, Fig. 3 | Compuesto de diez tetraedros regular |  |
 |
| 23 | Fg1 | 8 9 12 | 31 Sexta estelación | 17 | Taf. X, Fig. 3 | Sexta estelación del icosaedro |  |
 |
| 24 | De1f1 | 4 6' 9 10 | 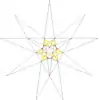 |  | ||||
| 25 | De1f1g1 | 4 6' 9 12 | 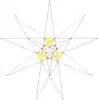 |  | ||||
| 26 | Ef1g1 | 7 9 12 | 28 Tercera estelación | 9 | Taf. VIII, Fig. 26 | Dodecaedro excavado | 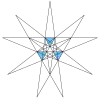 |
 |
| 27 | De2 | 3 6 7 | 5 | 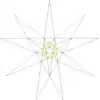 |
 | |||
| 28 | Ef2 | 5 6 8 | 18 | Taf.IX, Fig. 20 |  |
 | ||
| 29 | Fg2 | 10 11 | 33 Octava estelación | 14 | Octava estelación del icosaedro |  |
 | |
| 30 | De2f2 | 36 8 | 34 Novena estelación | 13 | Mediano icosaedro triámbico o gran icosaedro triámbico |
 |
 | |
| 31 | De2f2g2 | 3 6 9' 11 | 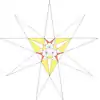 |  | ||||
| 32 | Ef2g2 | 5 6 9' 11 | 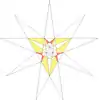 |  | ||||
| 33 | f1 | 5' 6' 9 10 | 35 Décima estelación | Décima estelación del icosaedro |  |
 | ||
| 34 | e1f1 | 3' 5 6' 9 10 | 36 Undécima estelación | Undécima estelación del icosaedro |  |
 | ||
| 35 | De1f1 | 4 5 6' 9 10 | 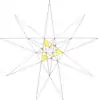 |  | ||||
| 36 | f1g1 | 5' 6' 9 10'12 | 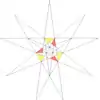 |  | ||||
| 37 | e1f1g1 | '3' 5 6' 9 10' 12 | 39 Decimocuarta estelación | Decimocuarta estelación del icosaedro |  |
 | ||
| 38 | De1f1g1 | 4 5 6' 9 10' 12 | 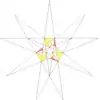 |  | ||||
| 39 | f1g2 | 5' 6' 8' 9' 10 11' | 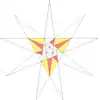 |  | ||||
| 40 | e1f1g2 | 3' 5 6' 8' 9' 10 11 |  |  | ||||
| 41 | De1f1g2 | 4 5 6' 8' 9' 10 11 | 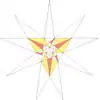 |  | ||||
| 42 | f1f2g2 | 5' 6' 7' 9' 10 11 | 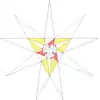 |  | ||||
| 43 | e1f1f2g2 | 3' 5 6' 7' 9' 10 11 | 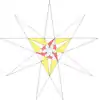 |  | ||||
| 44 | De1f1f2g2 | 4 5 6' 7' 9' 10 11 |  |  | ||||
| 45 | e2f1 | 4' 5' 6 7 9 10 | 40 Decimoquinta estelación | Decimoquinta estelación del icosaedro |  |
 | ||
| 46 | De2f1 | 3 5' 6 7 9 10 | 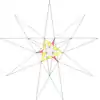 |  | ||||
| 47 | Ef1 | 5 6 7 9 10 | 24 Compuesto de cinco tetraedros |
7 (6: a izquierda) |
Taf. IX, Fig. 11 | Compuesto de cinco tetraedros regular (a derecha) |  |
 |
| 48 | e2f1g1 | 4' 5' 6 7 9 10' 12 | 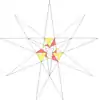 |  | ||||
| 49 | De2f1g1 | 3 5' 6 7 9 10' 12 | 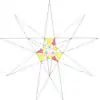 |  | ||||
| 50 | Ef1g1 | 5 6 7 9 10' 12 | 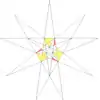 |  | ||||
| 51 | e2f1f2 | 4' 5' 6 8 9 10 | 38 Decimotercera estelación | Decimotercera estelación del icosaedro |  |
 | ||
| 52 | De2f1f2 | 3 5' 6 8 9 10 |  |  | ||||
| 53 | Ef1f2 | 5 6 8 9 10 | 15 (16: a izquierda) | 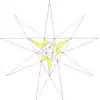 |  | |||
| 54 | e2f1f2g1 | 4' 5' 6 8 9 10' 12 | 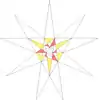 |  | ||||
| 55 | De2f1f2g1 | 3 5' 6 8 9 10' 12 | 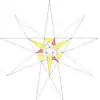 |  | ||||
| 56 | Ef1f2g1 | 5 6 8 9 10' 12 | 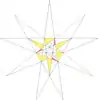 |  | ||||
| 57 | e2f1f2g2 | 4' 5' 6 9' 10 11 | 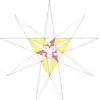 |  | ||||
| 58 | De2f1f2g2 | 3 5' 6 9' 10 11 | 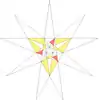 |  | ||||
| 59 | Ef1f2g2 | 5 6 9' 10 11 |  |  |
Véase también
- Modelos de poliedros de Wenninger. El libro de Wenninger Polyhedron models incluye 21 de estas estelaciones.
- Sólidos con simetría icosaédrica
Referencias
Bibliografía
- Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte. Leipzig: B. G. Treubner. ISBN 978-1-4181-6590-1. (en alemán)
- WorldCat Inglés: Polígonos y poliedros: teoría e historia. Fotografías de modelos: Tafel VIII (Plate VIII), etc. Alta resolución. escanea.
- Harold Scott MacDonald Coxeter, Patrick du Val, H.T. Flather, JF Petrie (1938) The Fifty-nine Icosahedra, estudios Universidad de Toronto, serie matemática 6: 1–26.
- Wenninger, Magnus J. (1983) Modelos de poliedros; Cambridge University Press, edición en rústica (2003). ISBN 978-0-521-09859-5.
- A. H. Wheeler (1924) "Ciertas formas del icosaedro y un método para derivar y designar poliedros superiores", Proceedings of the Congreso Internacional de Matemáticos, Toronto, vol. 1, págs. 701–708.
Enlaces externos
- Ejemplo de estelaciones del icosaedro
- Las cincuenta y nueve estelaciones del icosaedro regular
- Weisstein, Eric W. «Fifty nine icosahedron stellations». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Echidnahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Estelaciones del icosaedro
- George Hart, 59 Stellations of the Icosahedron - Archivos VRML 3D.