Tipi de Cantor
En mathématiques, le tipi de Cantor, ou éventail de Knaster-Kuratowski[1], est un espace topologique particulier : il est connexe mais quand on le prive de son sommet, il devient totalement discontinu.
Pour les articles homonymes, voir Éventail (homonymie).
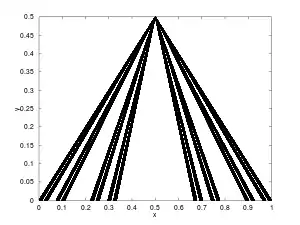
Le tipi de Cantor, ou éventail de Knaster–Kuratowski
Définition
Soient
- C l'ensemble de Cantor,
- p le point (1/2, 1/2) du plan ℝ2 et
- pour tout élément c de C, X(c) l'ensemble des points situés sur le segment de droite qui relie (c, 0) à p et dont l'ordonnée est
- rationnelle si c est une extrémité de l'un des intervalles supprimés lors de la construction de l'ensemble de Cantor,
- irrationnelle sinon.
L'éventail de Knaster-Kuratowski, de sommet p, est la réunion Y des X(c) quand c parcourt C (vue comme partie du plan munie de la topologie induite).
Le sous-espace Y\{p} est totalement discontinu, mais pas « totalement séparé » : deux points situés sur un même X(c) ne sont pas séparés par un ouvert-fermé[2],[3]. Sa dimension topologique est 1[4].
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Knaster–Kuratowski fan » (voir la liste des auteurs).
- Bronisław Knaster et Kazimierz Kuratowski, « Sur les ensembles connexes », Fundamenta Mathematicae, vol. 2, 1921, p. 206-255 : p. 233
- (en) Lynn Arthur Steen et J. Arthur Seebach, Jr., Counterexamples in Topology, Dover, (1re éd. Springer, 1978) (ISBN 978-0-486-68735-3), contre-exemples 128 et 129.
- (en) Dennis Pixton, Totally disconnected and zero dimensional metric spaces, Math 479 - Spring 2011, Real Analysis II, Binghamton University.
- (en) Keio Nagami, Dimension theory, Academic Press, , 256 p. (ISBN 978-0-12-513650-1, lire en ligne), p. 54, exemple 9.12.
- Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.