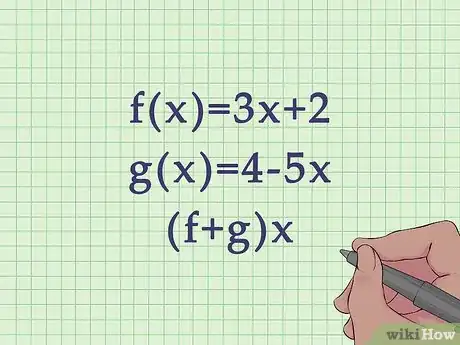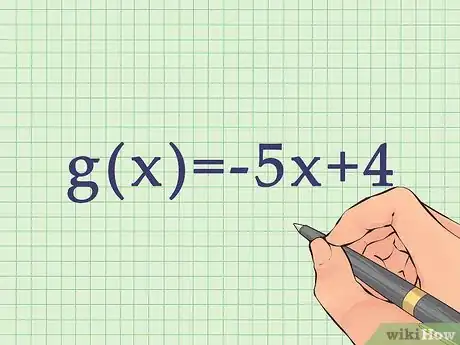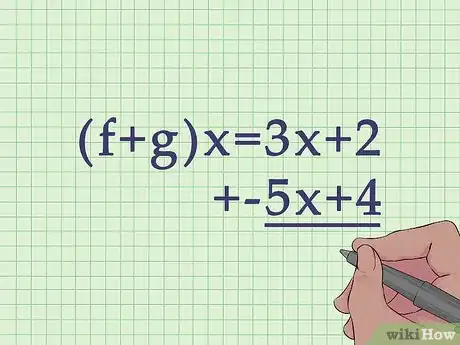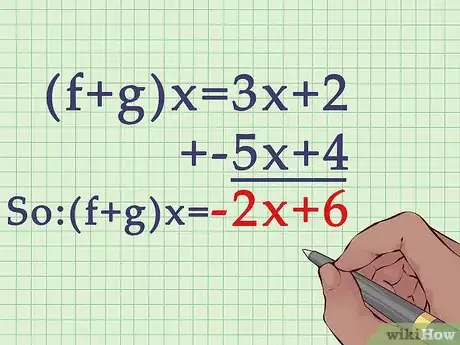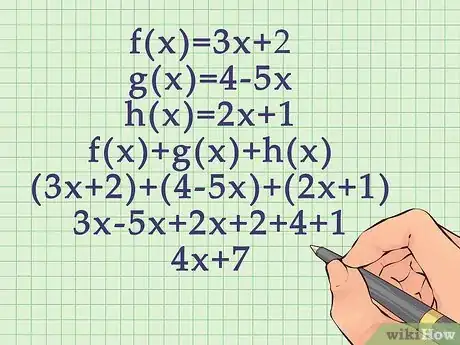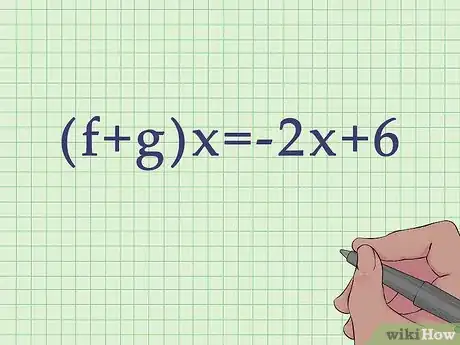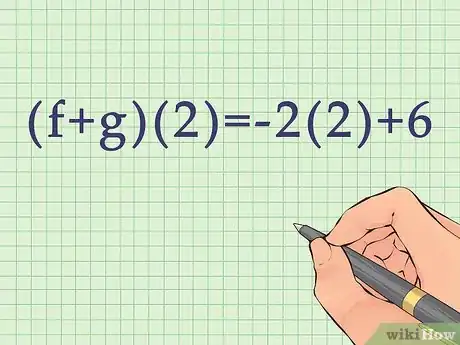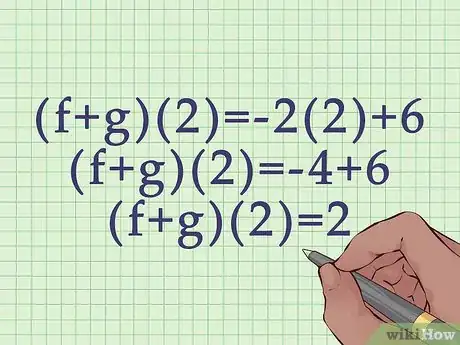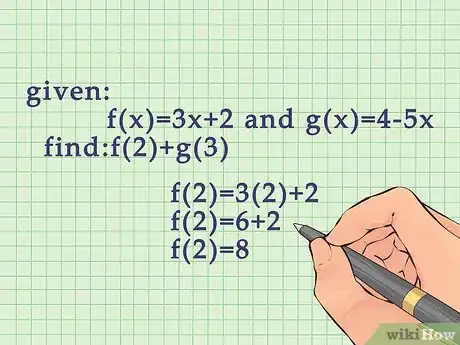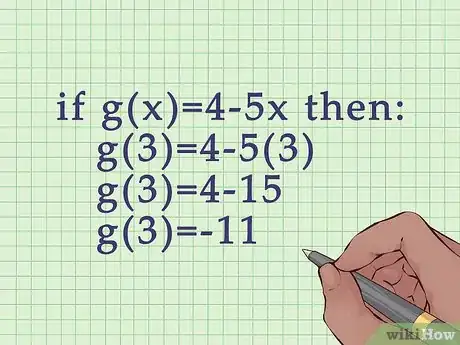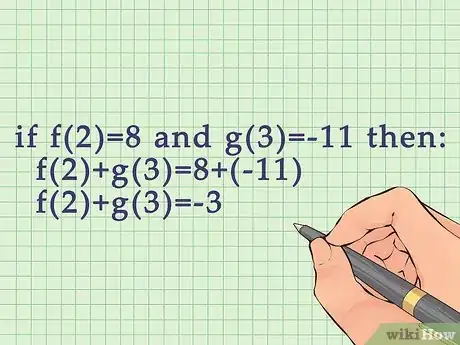How to Add and Subtract Functions

Co-authored by wikiHow Staff

Last Updated: February 17, 2023

Often you will use a function to describe curves and lines on a coordinate graph, as a function shows the relationship between the x and y coordinates. Just as you can add and subtract numbers, you can add or subtract functions. You might need to add or subtract functions when working with differing rates, scales, or measurements. Performing simple operations on functions is no more complicated than performing those operations on numbers.

Method 1

Method 1 of 3:

Adding or Subtracting Functions without an Input

1
Write out the functions that are being added or subtracted. Functions are usually stated as f(x) = relationship, where x is the variable input, and the relationship is stated as a formula for the variable x. ^{[1]
X
Research source} Since you are adding or subtracting more than one function, they will be labeled differently, most likely $f(x)$ $f(x)$ and $g(x)$ $g(x)$ .
- For example, you might be asked to add the function $f(x)=3x+2$ , and the function $g(x)=4-5x$ .
- If you are being asked to add, you will often be asked to find $(f+g)x$ .
- If you are being asked to subtract, you will often be asked to find $(f-g)x$ .
2
Reorder the functions by degree of terms. This means ordering the formula by exponents, beginning with the largest exponent ( $x^{3},x^{2},x,$ $x^{{3}},x^{{2}},x,$ etc.). If there is no exponent, order the first-degree term first (x), followed the constants (numbers without variables).
- For example, the function $g(x)$ would be reordered as $-5x+4$ . The f(x) function is already ordered by degree of terms.
Advertisement
3
Create an addition or subtraction problem using the two formulas. You can add/subtract horizontally or vertically, since you have ordered the functions by terms.^{[2]
X
Research source}
- For example, your function can be set up as $(f+g)x=(3x+2)+(-5x+4)$ ,
  or it could be set up vertically, with like terms lined up:
  $+{\begin{matrix}3x&+&2\\-5x&+&4\end{matrix}}$ .
4
Add or subtract like terms. It is helpful to add/subtract in order of the degree of terms, beginning with the highest exponent (if any). ^{[3]
X
Research source}
- For example, for $(f+g)x=(3x+2)+(-5x+4)$ , you would first add the first-degree terms:
  $3x+(-5x)=-2x$ .
  Second, you would add the constants:
  $2+4=6$ .
  So $(f+g)x=-2x+6$ .
5
Follow the same process for adding or subtracting more than two functions. Adding or subtracting functions is always just a matter of adding/subtracting the like terms in the relationship formulas.

Method 2

Method 2 of 3:

Adding or Subtracting Functions with the Same Input

1
Add or subtract the functions, as described in Method 1. This will give you the formula relationship for your variable input (x).^{[4]
X
Research source}
- For example, you might find that $(f+g)x=-2x+6$ .
2
Plug in the variable. Remember, this method only works if you are adding/subtracting functions with the same input variable.
- For example, you might be asked to find $(f+g)(2)$ . Your added function would then look like $(f+g)(2)=-2(2)+6$ .
3
Complete the calculation. Remember to use the order of operations.
- For example:
  $(f+g)(2)=-2(2)+6$
  $(f+g)(2)=-4+6$
  $(f+g)(2)=2$ .

Method 3

Method 3 of 3:

Adding or Subtracting Functions with Different Inputs

1
Plug the appropriate variable into the first function and solve. Since you are working with two different variables (inputs), you cannot add the formulas and plug in one input, you have to complete one function at a time.^{[5]
X
Research source}
- For example, if you are given $f(x)=3x+2$ and $g(x)=4-5x$ , and are asked to find $f(2)+g(3)$ , you would start by finding $f(2)$ . When you plug in the 2, you get:
  $f(2)=3(2)+2$
  $f(2)=6+2$
  $f(2)=8$ .
2
Plug the appropriate variable into the second function and solve. Make sure you are plugging in the correct variable to the correct function.
- For example, if $g(x)=4-5x$ , then:
  $g(3)=4-5(3)$
  $g(3)=4-15$
  $g(3)=-11$
3
Add or subtract the two outputs. The result will be the sum or difference of the two functions, given the provided variables.^{[6]
X
Research source}
- For example, if $f(2)=8$ and $g(3)=-11$ , then:
  $f(2)+g(3)=8+(-11)$
  $f(2)+g(3)=-3$ .

Community Q&A

Question

How do I combine 2w - 12 + w + 2?

Donagan

Top Answerer

Combine the terms with the variable in them, and combine the constant terms, then combine the results: 2w + w = 3w. -12 + 2 = -10. Combining 3w and -10 gives you 3w - 10.
Question

What do I have to remember when subtracting functions?

Community Answer

By far the most common mistake is carelessness in distributing the minus through the terms of g, resulting in some term having the wrong sign. Fortunately, this is an easy one to find and fix by picking 1 or 2 easy values of x and spot checking f(x), g(x), and (f-g)(x) at those specific points. A more subtle technicality is caused by domain mismatches. Recall that (f-g)(4) is only defined when both f(4) and g(4) are defined, even if (f-g)(x) looks algebraically like it should be defined as x=4.
Question

How do I add and subtract fractions?

Donagan

Top Answerer

See Add and Subtract Like Fractions and Add and Subtract Fractions With Unlike Denominators.