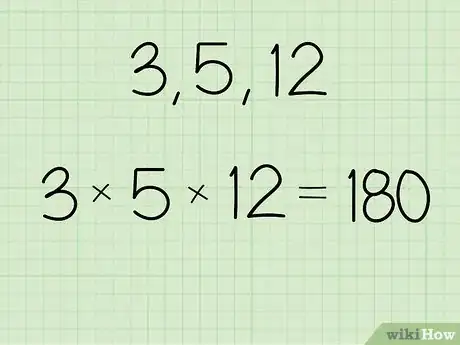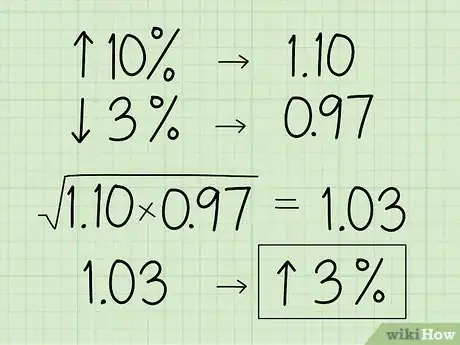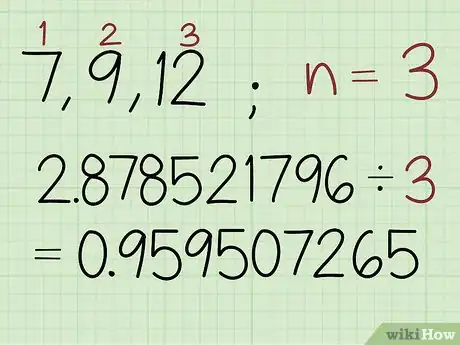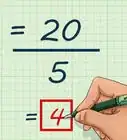This article was co-authored by wikiHow staff writer, Hunter Rising. Hunter Rising is a wikiHow Staff Writer based in Los Angeles. He has more than three years of experience writing for and working with wikiHow. Hunter holds a BFA in Entertainment Design from the University of Wisconsin - Stout and a Minor in English Writing.
This article has been viewed 854,708 times.
Learn more...
The geometric mean is another way to find the average value of a number set, but instead of adding the values and dividing like you would to find the arithmetic mean, you multiply them together before taking the root. The geometric mean can be used to calculate average rates of return in finances or show how much something has grown over a specific period of time. In order to find the geometric mean, multiply all of the values together before taking the nth root, where n equals the total number of values in the set. You can also use the logarithmic functions on your calculator to solve the geometric mean if you want.
Steps
Geometric Mean Help
Finding the Geometric Mean of a Value Set
-
1Multiply the values you want to find the geometric mean for. You can either use a calculator or do the math by hand when you find the product. Multiply all of the numbers in the set you’re calculating so you can find the product. Write down the product so you don’t forget it.[1]
- For example, if the value set is 3, 5, and 12, then you would write: (3 x 5 x 12) = 180.
- For another example, if you want to find the geometric mean for the set 2 and 18, then write: (2 x 18) = 36.
-
2Find the nth root of the product where n is the number of values. Count how many values are in the set you’re calculating the geometric mean for the value n. Use the n value to determine which root you need to take of the product. For example, take the square root if you have 2 values, cube root if you have 3 values, and so on. Use your calculator to solve the equation and write down your answer.[2]
- For example, for the set of 3, 5, and 12, write: ∛(180) ≈ 5.65.
- In the second example with a set of 2 and 18, write: √(36) = 6.
Variation: You can also write the value as an exponent 1/n if it's easier to type in your calculator. For example, for the set 3, 5, and 12, you can write (180)1/3 instead of ∛(180).
Advertisement -
3Convert percentages to their decimal multiplier equivalents. If the number set is written out as increases or decreases in percentages, avoid using the percent value in the geometric mean since it will skew your results. If the percent is an increase, move the decimal point 2 spaces to the left and add 1 to it. If there’s a percent decrease, then move the decimal point 2 places to the left and subtract it from 1.[3]
- For example, say you want to find the geometric mean of the value of an object that increases by 10%, and then falls by 3%.
- Convert 10% to a decimal and add 1 to it to get 1.10.
- Then convert 3% to a decimal and subtract it from 1 to get 0.97.
- Use the 2 decimal values to find the geometric mean: √(1.10 x 0.97) ≈ 1.03.
- Convert the number back to a percent by moving the decimal point 2 places to the right and subtracting 1 from it to find a total of a 3% increase in value.
Calculating Geometric Mean with Logarithms
-
1Add the logarithmic values for each number in the set. The LOG function takes a value out of base-10 and determines how many times you need to multiply 10 together to equal that value. Locate the LOG function on your calculator, which usually is on the left side of the keypad. Click the LOG button and enter the first value in the set. Type in a “+” before putting in LOG for your second value. Continue separating the LOG functions for each value with a plus sign before finding the sum.[4]
- For example, with a set of 7, 9, and 12, you would type in log(7) + log(9) + log(12) before hitting “=” on your calculator. When you solve the functions, your sum will be about 2.878521796.
- You may also calculate each of the logarithms separately before adding the answers together.
-
2Divide the sum of the logarithmic values by the number of values in the set. Count the number of values in your set and then divide the sum you just found by that number. The answer you get will be the logarithmic value of the geometric mean.[5]
- In this example, there’s a set of 3 numbers, so type in: 2.878521796 / 3 ≈ 0.959507265.
-
3Take the antilog of the quotient to determine the geometric mean. The antilog function is the inverse of the LOG function on your calculator and it converts the value back to base-10. Look for the symbol “10x” on your calculator, which is usually a secondary function of the LOG button. Press the “2nd” button in the top left corner of the calculator followed by the LOG button to activate the antilog. Type in the quotient you found in the last step before solving the equation.[6]
- For this example, your calculator will read: 10(0.959507265) ≈ 9.11.
Community Q&A
-
QuestionHow do I identify average numbers geometric mean, arithmetic mean and harmonic mean?
DonaganTop AnswererSee wikiHow's articles on each of those subjects. -
QuestionWhat is the geometric mean of 2, 4, 16, and 32?
Community AnswerTo make this trivially easy, use logarithms Base 2. Then the logarithms are 1, 2, 4, and 5. The simple average of those logarithms is 3, so the geometric mean of 2, 4, 16, and 32 is 2^3 = 8. -
QuestionHow do I find the geometric mean of 3 and 7?DonaganTop Answerer3 x 7 = 21. √21 = 4.58.
Things You’ll Need
- Calculator
References
- ↑ https://www.mathsisfun.com/numbers/geometric-mean.html
- ↑ https://www.mathsisfun.com/numbers/geometric-mean.html
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.cuemath.com/data/geometric-mean/
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
- ↑ https://www.cuemath.com/data/geometric-mean/
- ↑ https://www.waterboards.ca.gov/water_issues/programs/swamp/docs/cwt/guidance/3413.pdf
About This Article
To calculate the geometric mean of 2 numbers, multiply those 2 numbers together, then calculate the square root of the resulting product. If you have 3 or more numbers, multiply all of the numbers together, then raise them to the power of 1 divided by n, where n is the total number of entries in the data set. To learn how to calculate the geometric mean of a data set using logarithms, read on!
