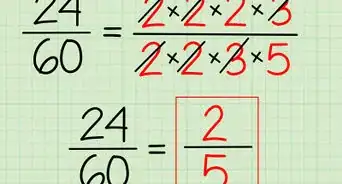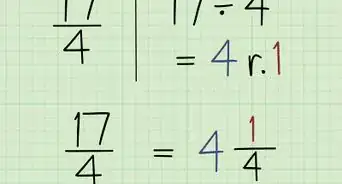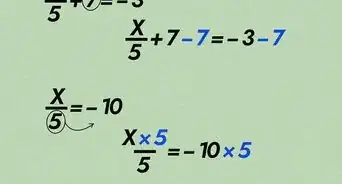This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
This article has been viewed 29,324 times.
A fraction containing a fraction in the numerator and denominator is a called a complex fraction. These types of expressions can be daunting, especially when they are algebraic expressions including variables. Simplifying them becomes easier when you remember that a fraction bar is the same thing as a division sign. To simplify a complex fraction, turn it into a division problem first. Then, divide as you would divide any fraction by a fraction. Remember to take the reciprocal of the second fraction and multiply. When working with variables, it is important to remember certain algebraic rules to simplify the expression.
Steps
Dividing a Fraction by a Fraction
-
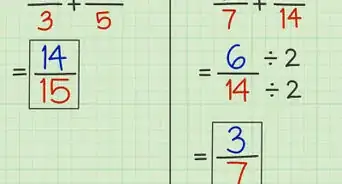
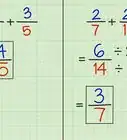
1Rewrite the complex fraction as a division problem. Remember that a fraction bar means “divided by,” so when you see a fraction over a fraction, you need to divide the top fraction by the bottom fraction.[1]
- For example, you might see . You can rewrite this as .
-
2Take the reciprocal of the second fraction. To divide a fraction by a fraction, you take the reciprocal of the second fraction, and you change the division sign to a multiplication sign. A reciprocal is a fraction in which the numerator and denominator are reversed.[2]
- For example:
becomes
Advertisement - For example:
-
3Rewrite the expression as a single fraction. Use parentheses to show the multiplication, but do not multiply any terms yet. Writing the expression this way may help you identify terms that can cancel.
- For example,.
-
4Simplify the expression. Use the normal rules for simplifying a rational expression to do this. Cancel out terms common to the numerator and denominator.[3]
- Remember that you cannot cancel out a single term (like ) from a binomial (like ).
- Also remember that if you have an term in the numerator, and an term in the denominator, you can cancel out one , and the in the denominator disappears, and the in the numerator becomes .
- For example, you can cancel an in the numerator and denominator in the expression :
-
5Complete the necessary multiplications. If you have any remaining parentheses in the numerator or denominator, simplify these by multiplying. The result will be your final simplified expression.
- For example, . So, .
Applying Algebra Rules to Complex Problems
-
1Use the FOIL method to multiply binomials. The FOIL method helps you remember to first multiply the first terms, then the outer terms, then the inner terms, then the last terms. When dividing a fraction by a fraction, this should be your last step after cancelling terms in the numerator and denominator.[4]
- For example, if you are simplifying the expression , after taking the reciprocal and combining terms, you end up with the expression . First, cancel the in the numerator and denominator, then multiply the binomials using the FOIL method:
- For example, if you are simplifying the expression , after taking the reciprocal and combining terms, you end up with the expression . First, cancel the in the numerator and denominator, then multiply the binomials using the FOIL method:
-
2Use the distributive property. You can use the distributive property to factor out a term. This might help you cancel terms. Conversely, you can use the distributive property to multiply a term into a binomial when you are simplifying your expression[5]
- For example, if you are simplifying the expression , after taking the reciprocal and combining terms, you end up with the expression . First, factor out a 2 from . Then you can cancel a 2 from the numerator and denominator. Then, simplify the expression by completing the multiplication:
- For example, if you are simplifying the expression , after taking the reciprocal and combining terms, you end up with the expression . First, factor out a 2 from . Then you can cancel a 2 from the numerator and denominator. Then, simplify the expression by completing the multiplication:
-
3Turn whole numbers into fractions. You will need to do this if the numerator or denominator of the complex fraction contains a whole number being added or subtracted to a fraction. Remember that to add or subtract fractions, the fractions need to have the same denominator. So, to turn a whole number in the top or bottom of a complex fraction into a fraction, multiply it by , where is the denominator of the fraction it is being added to or subtracted from.[6]
- For example, if you have , you would change the 2 into a fraction by multiplying it by :
- For example, if you have , you would change the 2 into a fraction by multiplying it by :
Community Q&A
-
QuestionHow do I multiply a positive fraction by a negative number?
 DonaganTop AnswererMultiply in the usual way, but place a negative sign in front of the answer (positive times negative equals negative).
DonaganTop AnswererMultiply in the usual way, but place a negative sign in front of the answer (positive times negative equals negative). -
QuestionHow do I solve 2x/3*9x/4x^2(square)y?
 DonaganTop AnswererIt can't be solved, because it's not an equation, but it can be simplified: (2x / 3)(9x / 4x²y) = 18x² / 12x²y = 3 / 2y.
DonaganTop AnswererIt can't be solved, because it's not an equation, but it can be simplified: (2x / 3)(9x / 4x²y) = 18x² / 12x²y = 3 / 2y.
References
- ↑ https://www.virtualnerd.com/algebra-1/algebra-background/fractions/complex-fractions/simplify-fraction-over-fraction
- ↑ https://www.mathsisfun.com/algebra/fractions-algebra.html
- ↑ https://www.khanacademy.org/math/arithmetic-home/arith-review-fractions/visualizing-equiv-frac/e/simplifying_fractions
- ↑ https://www.mathwarehouse.com/algebra/polynomial/foil-method-binomials.php
- ↑ https://www.coolmath.com/prealgebra/06-properties/05-properties-distributive-01
- ↑ https://www.khanacademy.org/math/cc-third-grade-math/imp-fractions/imp-fractions-and-whole-numbers/v/whole-numbers-as-fractions
-Step-1-Version-2.webp)


-Step-2-Version-2.webp)

-Step-3-Version-2.webp)

-Step-4-Version-2.webp)







-Step-5-Version-2.webp)


-Step-6-Version-2.webp)






-Step-7-Version-2.webp)







-Step-8-Version-2.webp)