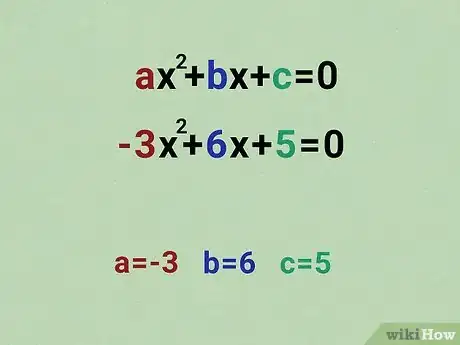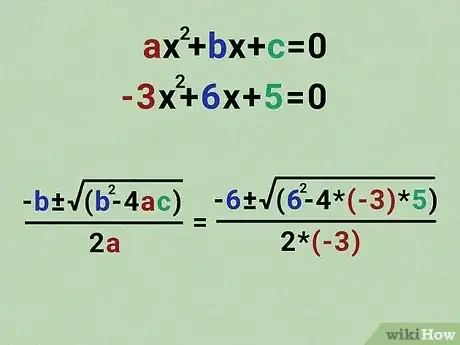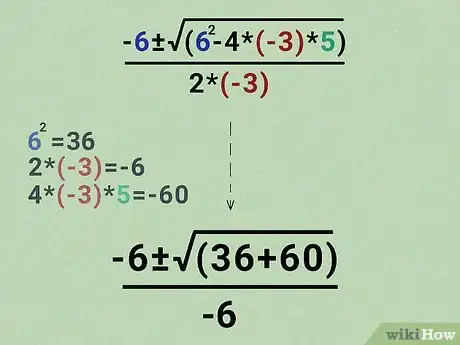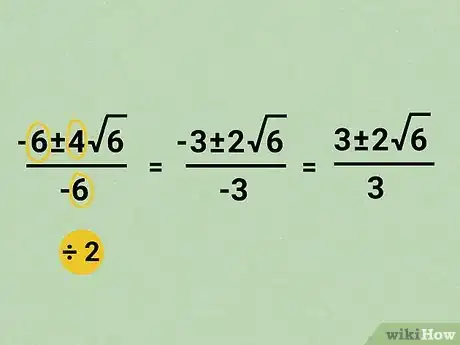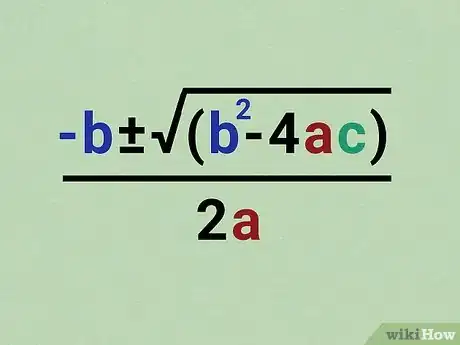This article was co-authored by David Jia and by wikiHow staff writer, Amber Crain. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
There are 7 references cited in this article, which can be found at the bottom of the page.
wikiHow marks an article as reader-approved once it receives enough positive feedback. In this case, several readers have written to tell us that this article was helpful to them, earning it our reader-approved status.
This article has been viewed 28,442 times.
You can use a few different techniques to solve a quadratic equation and the quadratic formula is one of them. The coolest thing about the formula is that it always works. You can apply it to any quadratic equation out there and you'll get an answer every time. That's not the case with the other techniques! The second coolest thing about the quadratic formula: it's easy to use. In this article, we'll walk you through the entire process from start to finish so you can crush your next algebra exam.
Steps
See if the equation equals zero.
-
If it does, the equation is ready for you to solve. You can't use quadratic formula until the equation equals
 . If the equation you’re looking at doesn’t equal zero, don’t worry. We'll show you how to convert it.[1]
X
Research source
. If the equation you’re looking at doesn’t equal zero, don’t worry. We'll show you how to convert it.[1]
X
Research source
- Here's a quadratic equation in standard form:

 [2]
X
Research source
[2]
X
Research source
- Here are 2 examples to demonstrate:
-

This equation is ready to solve because it equals .
. -

This equation is not ready to solve just yet. We need to convert it first.
-
- Here's a quadratic equation in standard form:
Convert the equation to standard form.
-
Standard form means the equation equals “0” and is ready to solve. It might sound complicated, but converting to standard form is pretty easy. You just need to move some things around a bit! It’s easier to show you, so check out these examples:[3] X Research source
- If an equation looks like this:

- Move the
 to the left side of the equal sign and put
to the left side of the equal sign and put  on the right side of the equal sign. Remember: numerals change from
on the right side of the equal sign. Remember: numerals change from  to
to  (or vice versa) when you move them to the other side of the equal sign.
(or vice versa) when you move them to the other side of the equal sign.
-
Our converted equation:

-
Our converted equation:
- Move the
- If an equation looks like this:

- Move all the terms to left side of the equal sign.
-
Our converted equation:

-
Our converted equation:
- Move all the terms to left side of the equal sign.
- If an equation looks like this:

- Undo the brackets to expand and move 5 to the left of the equal sign.
-
Our converted equation:

-
Our converted equation:
- Undo the brackets to expand and move 5 to the left of the equal sign.
- If an equation looks like this:
Identify the coefficients.
-
The coefficients are the a, b, and c in the standard form equation. Remember, the standard formula is

 . Our equation in standard formula is
. Our equation in standard formula is  . All you have to figure out a, b, and c.[4]
X
Research source
. All you have to figure out a, b, and c.[4]
X
Research source
- The coefficients in our equation:
- The coefficients in our equation:
Plug the coefficients into the quadratic formula.
-
Replace the a, b, and c in the quadratic formula with our coefficients. This part is easy! Just switch out the letters with the coefficients.[5] X Research source
- Remember, the quadratic formula looks like this:
 ± √(
± √(

- Our coefficients:
 ,
,  , and
, and 
- Our equation after inserting the coefficients:
 ± √(
± √(

- Remember, the quadratic formula looks like this:
Use the order of operations to simplify the formula.
-
Just do the math in the equation as you normally would. Now that all the coefficients have a numerical value, you can do the simple math in the equation.[6] X Research source

-
 x
x 
-
 x
x 
-
 x
x  =
= 
- You end up with:
 ± √
± √

- Then, simplify once more:
 ± √
± √

- Then, simplify once more:
- You end up with:
Simplify the radical.
-
The radical is the number inside √ which is 96. To simplify, find the prime factorization of the number inside the radical.[7] X Research source "Prime factorization" means dividing the number by 2 (the first prime number). Then, continue dividing by 2 until you get a decimal or remainder. At that point, divide by 3, 5, 7, etc. until all you have left are prime numbers.[8] X Research source
- Here's the prime factorization of 96: 2 x 2 x 2 x 2 x 2 x 3 = 96.
- Group the pairs: (2 x 2) (2 x 2). There are four 2s, so 4 goes outside the radical sign.
- Multiply what's left: (2 x 3) = 6. This goes inside the radical sign.
- So √
 simplified = 4√
simplified = 4√
- Putting it all together:
 ± 4√
± 4√

- Putting it all together:
- So √
- Here's the prime factorization of 96: 2 x 2 x 2 x 2 x 2 x 3 = 96.
Reduce the problem.
-
Our equation can be reduced by 2. -6, 4, and 6 are all divisible by 2. That means the equation can be reduced by 2. Divide each number by 2:
- -6 ÷ 2 = -3
- 4 ÷ 2 = 2
- 6 ÷ 2 = 3
- The reduced equation:
 ± 2√
± 2√
 or
or  ± 2√
± 2√

(both answers are correct because of the ± sign)- These are your final answers.[9] X Research source
- The reduced equation:
Circle your answer(s).
Memorize the quadratic formula.
-
The quadratic formula is
 ± √(
± √(
 . You'll need to memorize the formula at some point (probably for the upcoming exam), so committing it to memory now isn't a bad idea. The formula might look a bit complicated at first glance, but we have some fun tips to help you out.
. You'll need to memorize the formula at some point (probably for the upcoming exam), so committing it to memory now isn't a bad idea. The formula might look a bit complicated at first glance, but we have some fun tips to help you out.
- Sing these lyrics to the tune of Pop Goes the Weasel:
X is equal to negative B
Plus or minus the square root
Of B-squared minus four A C
All over two A - If songs aren't your thing, try memorizing this story instead:
A negative boy was thinking yes or no about going to a party.
At the party, he talked to a square boy but not to the 4 awesome cats.
It was all over at 2 am.[10] X Research source
- Sing these lyrics to the tune of Pop Goes the Weasel:
You Might Also Like










References
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/quad_formula/quad_formula.html
- ↑ https://www.youtube.com/watch?v=i7idZfS8t8w&t=59s
- ↑ https://www.mathsisfun.com/algebra/quadratic-equation.html
- ↑ https://www.youtube.com/watch?v=i7idZfS8t8w&t=129s
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/quad_formula/quad_formula.html
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/quad_formula/quad_formula.html
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/radicals/simplify/simplifying.html
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/radicals/simplify/images/examples/prime_factorization.html
- ↑ https://www.chem.tamu.edu/class/fyp/mathrev/mr-quadr.html
About This Article