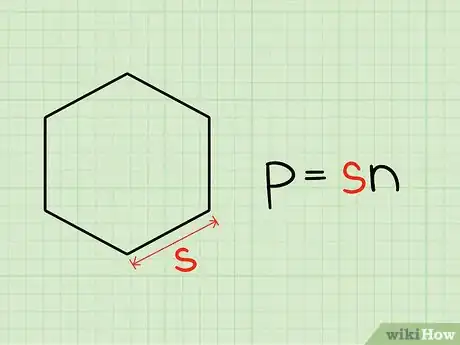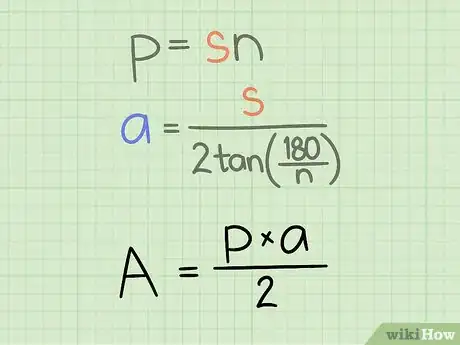wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 23 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 395 588 veces.
Un polígono regular es una figura convexa bidimensional con lados congruentes y ángulos del mismo valor. Muchos polígonos, como los cuadriláteros o los triángulos, tienen fórmulas sencillas con las que se puede hallar su área, pero si vas a trabajar con un polígono que tiene más de cuatro lados, entonces lo mejor es utilizar la fórmula que te presentaremos en el presente artículo, que utiliza la forma del apotema y el perímetro del polígono para calcular el área. Con un poco de esfuerzo, puedes hallar el área de cualquier polígono regular en tan solo unos minutos.
Pasos
Parte 1
Parte 1 de 2:Calcular el área
-
1Calcula el perímetro. El perímetro es la longitud total del contorno de cualquier figura bidimensional. En los polígonos regulares, se puede calcular multiplicando la longitud de un lado del polígono por el número de lados (n).[1]
-
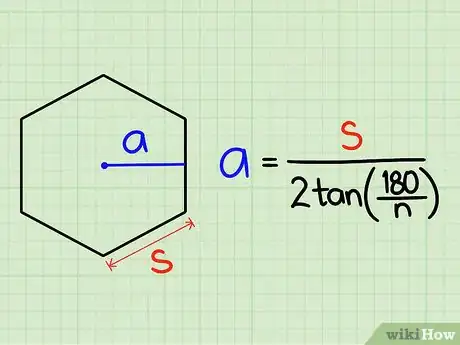
2Determina el valor de la apotema. La apotema de un polígono regular es la menor distancia posible desde el punto central del polígono hacia uno de sus lados, creando un triángulo rectángulo. Calcular la apotema es un poco más complicado que calcular el perímetro.
- La fórmula para calcular la longitud de la apotema es la siguiente: la longitud del lado (s) dividida entre 2 veces la tangente (tan) de 180° divido por el número de lados (n).
-
3Conoce la fórmula para calcular el área de un polígono. El área de cualquier polígono regular está dada por la fórmula:Área = (a x p)/2, donde a es la longitud de la apotema y p es el perímetro del polígono.
-
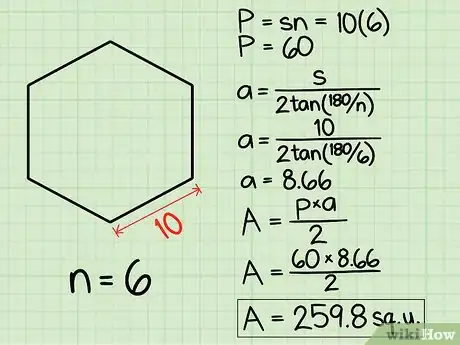
4Reemplaza los valores de a y p en la fórmula y obtén el área. Como ejemplo, vamos a utilizar un hexágono (6 lados) con un lado (s) con una longitud de 10.
- El perímetro es 6 x 10 (n x s), igual a 60 (entonces, p = 60).
- La apotema se calcula por su propia fórmula, sustituyendo 6 y 10 por n y s. El resultado de 2tan (180/6) es 1,1547, y luego 10 dividido entre 1,1547 da 8,66.
- El área del polígono es Área = a x p / 2, o 8,66 multiplicado por 60 y dividido entre 2. La solución es un área de 259,8 unidades.
- También ten en cuenta que no hay paréntesis en la ecuación del "Área", así que 8,66 dividido entre 2 y multiplicado por 60 te dará el mismo resultado, así como 60 dividido entre 2 y multiplicado por 8,66 te dará el mismo resultado.
Parte 2
Parte 2 de 2:Comprender los conceptos de una forma diferente
-
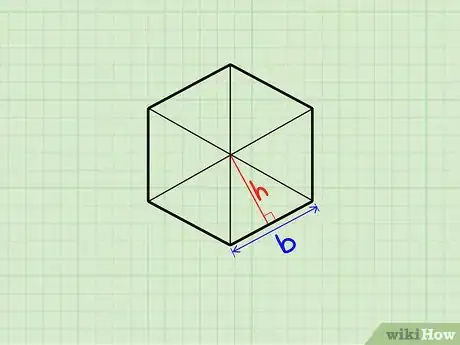
1Ten en cuenta que un polígono regular puede verse como una suma de varios triángulos. Cada lado representa la base de un triángulo y hay la misma cantidad de triángulos y de lados en el polígono. Todos los triángulos son iguales en longitud de la base, altura y área.[2]
-
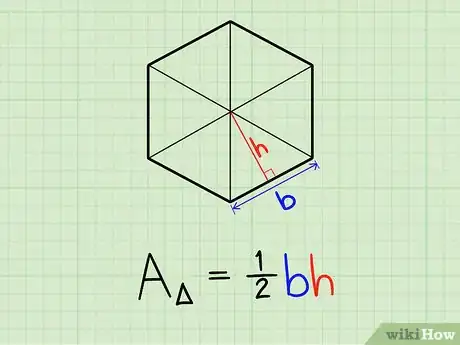
2Recuerda la fórmula para hallar el área de un triángulo. El área de cualquier triángulo es 1/2 por la longitud de la base (la cual es la longitud del lado en el polígono) multiplicado por la altura (la cual es la apotema en un polígono regular).[3]
-
3Observa las similitudes. La fórmula para hallar el área de un polígono regular es 1/2 por la apotema multiplicado por el perímetro. El perímetro es la longitud de un lado multiplicada por el número de lados (n); en un polígono regular, n también representa el número de triángulos que conforman la figura. Por lo tanto, la fórmula es lo mismo que el área de un triángulo multiplicada por el número de triángulos que conforman el polígono.[4]
Consejos
- Para más información sobre cómo trabajar con raíces cuadradas, revisa estos artículos: "Cómo multiplicar raíces cuadradas" y "Cómo dividir raíces cuadradas".
- Si tienes un dibujo del polígono separado en triángulos y tienes el área de uno de ellos, entonces no tienes que hallar la apotema. Simplemente toma el área del triángulo y multiplícala por el número de lados del polígono.