Cómo calcular probabilidades

El concepto matemático de cuotas está relacionado, aunque es distinto del concepto de probabilidad. En términos simples, las cuotas son la forma en la que se expresa una relación entre un número de resultados favorables contra el número de resultados desfavorables en una situación dada. Por lo general, se expresan como una proporción (como por ejemplo 1 : 3 o 1/3). Calcular cuotas es un elemento de estrategia muy importante en muchos juegos de azar, como la ruleta, las carreras de caballos y el póquer. Independientemente de que seas un apostador experimentado o simplemente alguien curioso, aprender a calcular cuotas puede hacer los juegos de azar una actividad mucho más divertida y rentable.

Parte 1

Parte 1 de 3:
Calcula cuotas básicas

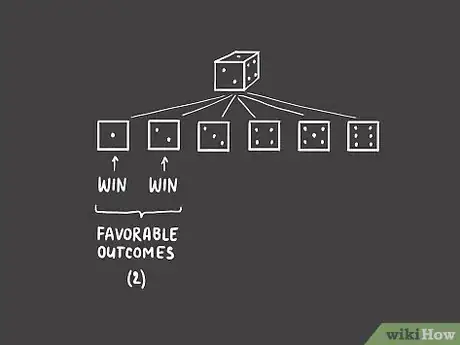
1
Determina el número de resultados favorables en la situación. Supongamos que vamos a apostar a lanzar un dado. En este caso, apostamos en el número en el que creemos que va a caer el dado después de lanzarlo. Supongamos que apostamos por sacar un uno o un dos. En este caso, existen dos posibilidades de que ganemos, si el dado cae en dos, ganamos, lo mismo que si el dado cae en uno. Por lo tanto, hay dos resultados favorables.
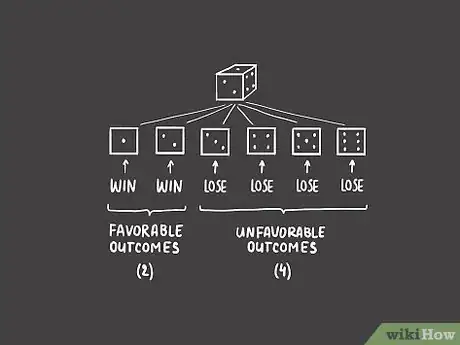
2
Determina el número de resultados desfavorables. En los juegos de azar, existe siempre la posibilidad de perder. Si apostamos a que vamos a sacar un uno o un dos, eso significa que perdemos si sacamos un tres, un cuatro, un cinco o un seis. Ya que podemos perder al sacar cualquiera de esos cuatro números, eso significa que existen cuatro resultados desfavorables.
- Otra forma de verlo es como número total de resultados posibles menos el número de resultados favorables. Al lanzar un dado, el número total de resultados posibles es igual a seis, uno por cada cara del dado. En nuestro ejemplo, restamos dos (el número de resultados favorables) de seis. 6 - 2 = 4, es decir, el número de resultados desfavorables.
- De forma similar, puedes restar el número de resultados desfavorables del número de resultados posibles para hallar el número de resultados favorables.
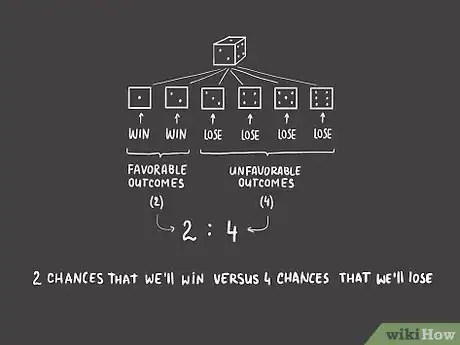
3
Expresa cuotas numéricamente. Generalmente, las cuotas se expresan como la relación entre resultados favorables y resultados desfavorables, normalmente utilizando dos puntos. En nuestro ejemplo, la cuota que expresa nuestra probabilidad de éxito es 2 : 4, dos posibilidades de ganar contra cuatro posibilidades de perder. Si dividimos ambos términos por el común múltiplo de dos, se puede simplificar como una fracción normal a 1 : 2. Esta relación se puede escribir como una "cuota de 1 a 2".
- Puedes representar esta relación como una fracción. En este caso, la cuota se expresa como 2/4, y se simplifica como 1/2. Nota: Una cuota de 1/2 no significa que tenemos la mitad (50%) de probabilidades de ganar. En realidad la probabilidad de éxito es del 33,3% (1/3). Recuerda que las cuotas son la relación entre los resultados favorables y los resultados desfavorables, no una medida numérica de las probabilidades que tenemos de ganar.
4
Aprender a calcular las cuotas en contra de que suceda un evento. La cuota 1 : 2 expresa la cuota a favor de éxito. Si queremos hallar la cuota que expresa nuestras opciones de obtener un resultado desfavorable, necesitamos hallar las cuotas en contra. Para hallar las cuotas en contra, simplemente invierte la proporción de la cuota a favor. 1 : 2 se convierte en 2 : 1.
- Si expresas la cuota en contra como una fracción, obtienes 2/1. Recuerda, como se dijo anteriormente, esta no es una expresión de tus probabilidades de perder, es la relación de resultados desfavorables en contra de los resultados favorables. Si fuera una expresión de tus probabilidades de perder, tendrías una probabilidad de perder de 200%, lo cual obviamente es imposible. De la siguiente forma es cómo se entiende el resultado de una cuota en contra. En realidad, tienes una probabilidad de perder de 66%, dos posibilidades de perder contra una posibilidad de ganar, significa 2 pérdidas / 3 posibles resultados = 0,66 = 66%.
5
Conoce la diferencia entre cuota y probabilidad. Los conceptos de cuota y probabilidad se encuentran relacionados, pero no son iguales. La probabilidad es una representación de la posibilidad de que cierto resultado suceda. Se halla dividiendo el número de resultados deseados sobre el número de resultados posibles. En nuestro ejemplo, la probabilidad (no la cuota) de que saquemos un uno o un dos (de un dado con seis caras) es 2 / 6 = 1 / 3 = 0,33 = 33%. Por lo que nuestra cuota a favor de 1 : 2 se convierte en una probabilidad de ganar del 33%.
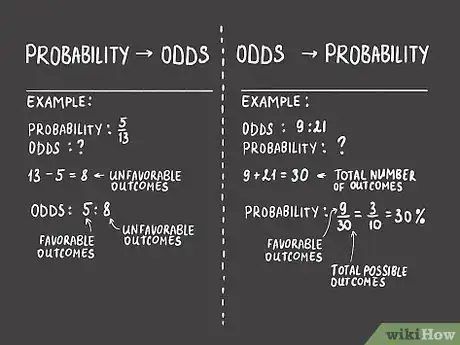
- Es fácil realizar la conversión entre probabilidades y cuotas. Para hallar la cuota dada una probabilidad, primero expresamos la probabilidad como una fracción (utilizaremos 5/13 como ejemplo). Resta el numerador (5) del denominador (13) : 13 - 5 = 8. La respuesta es el número de resultados favorables. La cuota se puede expresar como 5 : 8, la relación entre los resultados favorables y los resultados desfavorables.^{[1]
  X
  Fuente de investigación}
- Para hallar la probabilidad dada una cuota, primero expresa la cuota como una fracción (utilizaremos 9 / 21 como ejemplo). Suma el numerador (9) al denominador (21): 9 + 21 = 30. La respuesta es el número total de posibles resultados. La probabilidad se puede expresar como 9/30 = 3/10 = 30%, el número de resultados favorables sobre el número total de posibles resultados.^{[2]
  X
  Fuente de investigación
  Ibid.}
- Una fórmula simple para calcular cuotas con una probabilidad es C = P / (1 - P). #* Una fórmula simple para calcular probabilidades con una cuota es P = C / (C + 1).^{[3]
  X
  Fuente de investigación}

Parte 2

Parte 2 de 3:
Calcula cuotas complejas

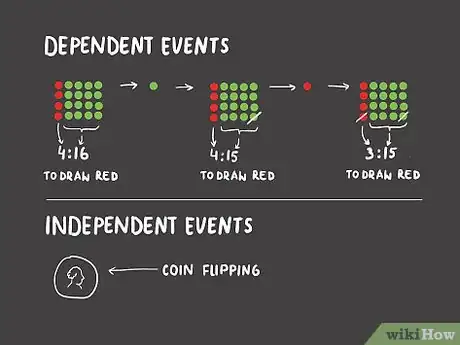
1
Comprende la diferencia entre eventos dependientes e independientes. En ciertos escenarios, las cuotas de cierto evento varían basado en los resultados de eventos pasados. Por ejemplo, si tienes una frasco con veinte canicas, de las cuales cuatro son rojas y dieciséis son verdes, tienes un cuota de 4 : 16 (1 : 4) de sacar una canica roja al azar. Supongamos que sacas una canica verde. Si no regresas la canica al frasco, en el próximo intento, tienes una cuota de 4 : 15 de sacar una canica roja. Luego, si sacas una canica roja, tienes una cuota de 3 : 15 (1 : 5) en el siguiente intento. Sacar una canica roja es un evento dependiente, las cuotas dependen de las canicas que se hayan sacado.
- Los eventos independientes son eventos cuyas cuotas no se ven afectadas por los eventos anteriores. Lanzar una moneda y obtener cara es un evento independiente, no tienes más probabilidad de sacar cara basado en los lanzamientos anteriores.
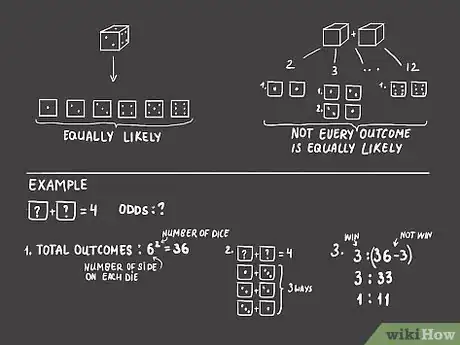
2
Determina cuando todos los resultados tienen las mismas posibilidades. Si lanzamos un dado, tenemos la misma posibilidad de obtener cualquier número del 1 al 6. Sin embargo, si lanzamos dos dados y sumamos sus números, tenemos la posibilidad de obtener cualquier número del 2 al 12, no todos los resultados tienen las mismas posibilidades. Solo hay una forma de sacar un dos (sacando un uno en ambos lanzamientos) y solo hay una forma de sacar un 12 (obteniendo 6 en ambos lanzamientos). Por el contrario, hay muchas formas de sacar un siete. Por ejemplo, puedes sacar un 1 y un 6, un 2 y un 5, un 3 y 4, etc. En este caso, las cuotas de cada suma deben reflejar el hecho de que algunos resultados son más probables que otros.
- Utilicemos un problema como ejemplo. Para calcular las cuotas para obtener un cuatro al sumar los números obtenidos al lanzar dos dados (por ejemplo, 1 y 3), primero calculamos el número total de posibles resultados. Cada dado tiene seis posibles resultados. Eleva el número de posibles resultados de cada dado a la potencia del número de dados que vas a utilizar: 6 (número de caras en cada dado)^{2(número de dados)} = 36 posibles resultados. A continuación, halla todas las formas posibles con las que puedes obtener cuatro con los dos dados: puedes sacar un 1 y un 3, un 2 y un 2 o un 3 y un 1, existen en total 3 formas en las que puedes sacar un cuatro. Por lo que la cuota para sacar un "cuatro" al sumar el resultado de ambos dados es 3 : (36-3) = 3 : 33 = 1 : 11.
- Las cuotas varían exponencialmente basado en el número de eventos que ocurran de forma simultánea. La cuota para obtener un "yahtzee" (sacar el mismo número al lanzar cinco dados) en un solo lanzamiento es muy pequeña, 6 : 6⁵ - 6 = 6 : 7770 = ¡1 : 1295!
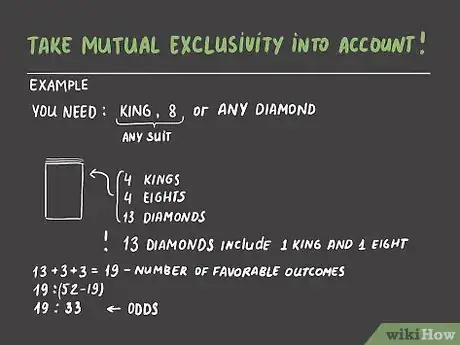
3
Ten en cuenta la exclusividad mutua. En ocasiones, ciertos resultados se pueden sobreponer, lo cual se debe ver reflejado en las cuotas. Por ejemplo, si juegas póquer y tienes en tu mano un nueve, un diez, una sota y una reina de diamantes, quieres que tu próxima carta sea un rey o un ocho de cualquier palo (para hacer una escalera) o de forma alternativa, cualquier diamante (para hacer un color). Supongamos que el repartidor saca la siguiente carta de una baraja estándar de cincuenta y dos cartas. Hay trece diamantes en la baraja, cuatro reyes y cuatro ocho. Sin embargo, el número total de resultados favorables no es 13 + 4 + 4 = 21. El trece de diamantes ya incluye el rey y el ocho de diamantes, no querrás contarlos dos veces. El número real de resultados favorables es 13 + 3 + 3 = 19. Por lo tanto, la cuota para obtener una carta para sacar una escalera o color es 19 : (52 - 19) o 19 : 33. ¡Nada mal!
- En la vida real, si ya tienes cartas en la mano, es muy raro que te repartan cartas de una baraja completa de cincuenta y dos cartas. Ten en cuenta que el número de cartas en la baraja disminuye a medida que se reparten las cartas. Además, si juegas contra otras personas, tienes que adivinar qué cartas tienen al hacer un estimado de tus cuotas. Esa es la parte divertida del póquer.

Parte 3

Parte 3 de 3:
Comprende las cuotas en las apuestas

1
Conoce los formatos más utilizados en los que se expresan las cuotas en las apuestas. Si te vas a adentrar en el mundo de las apuestas, es importante que sepas que las cuotas en las apuestas normalmente no reflejan las verdaderas "cuotas" matemáticas de que determinado evento ocurra. En lugar de eso, las cuotas en las apuestas, especialmente en juegos como las carreras de caballos o las apuestas deportivas, reflejan el pago que dará el corredor de apuestas si la apuesta es exitosa. Por ejemplo, si apuestas $100 en un caballo con cuota de 20:1 en contra, eso no significa que hay veinte resultados donde el caballo pierda y uno donde gane. Significa que te pagarán 20 veces tu apuesta original, en este caso, ¡$2000! El formato para expresar este tipo de cuotas a veces varía regionalmente. Aquí tienes varias formas no estándar en las que se expresan las cuotas en las apuestas:
- Cuotas decimales (o "formato europeo"). Son bastante fáciles de entender. Las cuotas decimales como su nombre lo indican, se expresan como un número decimal, como por ejemplo 2,50. Este número es la relación de pago frente a la apuesta original. Por ejemplo, con una cuota de 2,50, si apuestas $100 y ganas, recibes $250 dólares, 2,5 veces tu apuesta original. En este caso, obtienes una ganancia de $150.
- Cuotas fraccionales (o "formato del Reino Unido"). Estas se expresan como una fracción, como por ejemplo 1/4. Representan la relación de ganancia (no de pago total) de una apuesta exitosa. Por ejemplo, si apuestas $100 en algo con una cuota fraccional de 1/4 y ganas, tu ganancia será 1/4 de la apuesta original, en este caso, el pago será de $125, obtienes una ganancia de $25 (1/4 de tu apuesta original).
- Cuotas americanas (o "money line"). Este tipo de cuota puede ser algo difícil de entender. Se expresan como un número precedido por un signo de menos o de más, como por ejemplo -200 o +50. Un signo de menos significa que el número representa cuánto dinero tienes que apostar para ganar $100. Un signo positivo significa que el número representa cuánto ganas si apuestas $100. ¡Es muy importante recordar esa distinción! Por ejemplo, si apostamos $50 con una cuota americana de -200, si ganamos, obtenemos un pago de $75, para una ganancia total de $25 (necesitamos apostar $200, si queremos ganar $100). Si apostamos $50 con una cuota americana de +200, obtenemos un pago de $150, para una ganancia total de $100 (si apuestas $100, la ganancia sería de $200).
  - En este tipo de cuota, un "100" (sin más ni menos) representa una apuesta uniforme, el dinero que apuestes será igual a la ganancia.
2
Comprende cómo se establecen las cuotas en las apuestas. Las cuotas que fijan los corredores de apuestas y los casinos no se calculan normalmente utilizando la probabilidad matemática de que suceda determinado evento. En lugar de eso, se definen cuidadosamente para que en el largo plazo, el corredor de apuestas o el casino ganen dinero, independientemente de los resultados a corto plazo. Ten en cuenta lo anterior cuando vayas a apostar, recuerda, al final, la casa siempre gana.
- Miremos un ejemplo. Una rueda de una ruleta estándar tiene 38 números, del 1 al 36, más el 0 y 00.^{[4]
  X
  Fuente de investigación}. Si apuestas a un espacio (supongamos 11), tienes una cuota a favor de 1 : 37. Sin embargo, el casino establece la cuota de pago en 35 : 1, si la bola cae en el 11, ganas 35 veces tu apuesta original. Ten en cuenta que la cuota de pago es ligeramente menor a la cuota a favor. Si al casino no estuviera interesado en hacer dinero, la cuota de pago sería 37 : 1. Sin embargo, al definir la cuota de pago ligeramente por debajo de la cuota real de victoria, el casino gana dinero gradualmente con el paso del tiempo, incluso si tiene que realizar un pago grande ocasional cuando la bola cae en 11.
3
No caiga presa de las falacias comunes al apostar. Apostar puede ser divertido, incluso adictivo. Sin embargo, ciertas estrategias de apuesta bastante extendidas que en principio parecen tener "sentido común", son desde el punto de vista matemático, completamente falsas. A continuación tienes algunas cosas que debes tener en cuenta cuando vayas a apostar:
- Nunca esperes una buena racha. Si has jugado póquer por más de una hora y no has sacado una sola mano buena, tal vez quieras quedarte en la mesa con la esperanza de que una escalera o una escalera real esté a "la vuelta de la esquina". Desafortunadamente, las cuotas no cambian con la cantidad de tiempo que llevas apostando. Las cartas se barajan al azar antes de repartirlas, por lo que si has sacado diez manos malas seguidas, tienes la misma probabilidad de obtener otra mano mala que si hubieras sacado cientos de manos malas seguidas. Esto se extiende a la mayoría de juegos de azar, como la ruleta, las máquinas tragamonedas, etc.
- Apegarse a una apuesta específica no incrementa las cuotas. Tal vez conozcas a alguien que tiene un "número de la suerte", aunque puede ser divertido apostar dinero en un número con un significado personal especial, en los juegos de azar, no tienes más probabilidades de ganar al apostar siempre al mismo número que al apostar a números diferentes. Los números de lotería, las máquinas tragamonedas y los números en la ruleta, son completamente aleatorios. Por ejemplo, en la ruleta, tienes la misma probabilidad de obtener un "9" tres veces seguidas que obtener cualquier otros tres números en un orden específico.
- Si te faltó muy poco para acertar al número ganador, no estuviste "cerca" de ganar. Si escogiste el número 41 para una lotería y el número ganador es el 42, es algo difícil de asimilar, ¡pero no te desanimes! Ni siquiera estuviste cerca. Dos números cercanos (como el 41 y el 42) no están unidos matemáticamente de ninguna forma en los juegos de azar.

Consejos

Revisa las reglas del juego específico que planeas jugar para conocer más información que te ayude a calcular las cuotas.
Calcular las cuotas de la lotería es mucho más difícil.
En internet puedes encontrar gráficos donde ya hayan calculado las cuotas.
Busca servicios web gratuitos que calculen las cuotas en tiempo real para que te guíen y sepas cómo los corredores de apuestas van a calcular las cuotas para los próximos eventos deportivos.

Advertencias

Debes saber que en las apuestas, tienes las probabilidades en contra. Esto aumenta cuando juegas un juego aleatorio que no depende de los resultados anteriores, como las máquinas tragamonedas.