wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 32 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
En este artículo, hay 12 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 1 308 185 veces.
El volumen de una figura es la medida de cuánto espacio tridimensional ocupa.[1] También puedes pensar en el volumen de una figura como cuánta agua (o aire, arena, etc.) podría albergar si se llenara por completo. Las unidades de volumen comunes incluyen los centímetros cúbicos (cm3), los metros cúbicos (m3), las pulgadas cúbicas (in3) y los pies cúbicos (ft3).[2] Este artículo te enseñará a calcular el volumen de seis formas tridimensionales diferentes que, a menudo, se encuentran en los exámenes de matemáticas, incluyendo los cubos, las esferas y los conos. Es posible que notes que muchas de las fórmulas para el volumen tienen similitudes que pueden hacer que sea más fácil recordarlas. ¡Observa si puedes descubrirlas!
Pasos
Método 1
Método 1 de 6:Calcular el volumen de un cubo
-
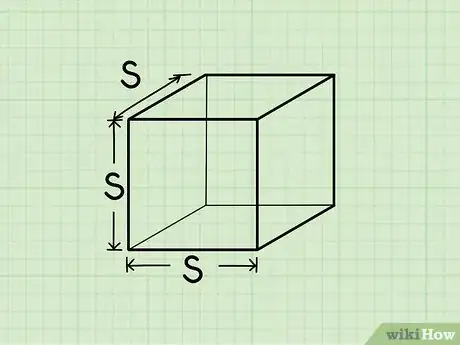
1Reconoce un cubo. Un cubo es una forma tridimensional que tiene seis caras cuadradas iguales.[3] En otras palabras, es una forma de caja con todos los lados iguales.
- Un dado de seis lados es un buen ejemplo de un cubo que podrías encontrar en casa. Los cubos de azúcar y los bloques de letras para niños también suelen ser cubos.
-
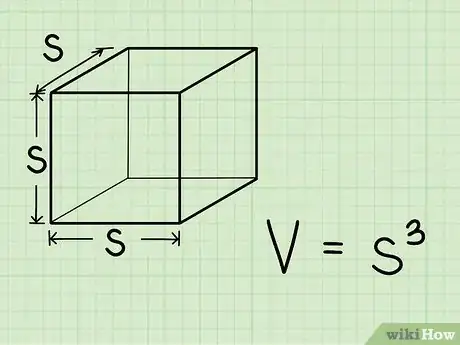
2Aprende la fórmula para el volumen de un cubo. Debido a que las longitudes de todos los lados de un cubo son iguales, la fórmula para el volumen de este es muy fácil. Es V = l3, en donde "V" es el volumen y "l" es la longitud de los lados del cubo.
- Para hallar s3, simplemente multiplica "s" por sí mismo 3 veces: s3 = s * s * s.
-
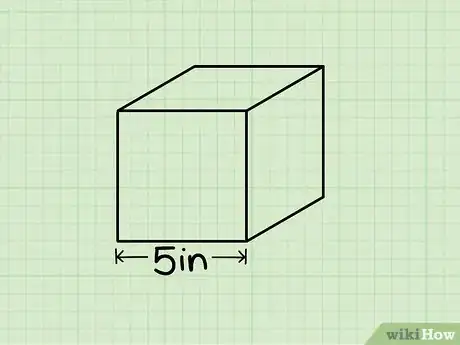
3Halla la longitud de un lado del cubo. Dependiendo de tu tarea, el cubo estará etiquetado con esta información o es posible que debas medir la longitud del lado con una regla. Recuerda que, debido a que es un cubo, las longitudes de todos los lados deben ser iguales, así que no importa cuál midas.
- Si no estás completamente seguro de que la figura sea un cubo, mide cada uno de los lados para determinar si son iguales. Si no lo son, tendrás que usar el método a continuación para calcular el volumen de un sólido rectangular.
-
4Sustituye la longitud del lado en la fórmula V = s3 y calcula. Por ejemplo, si encuentras que la longitud de los lados del cubo es 12 cm (5 pulgadas), debes escribir la fórmula como sigue: V = (12 cm)3. 12 * 12 x * 12 = 1728 cm3 (125 pulgadas cúbicas), ¡el volumen de nuestro cubo!
-
5Asegúrate de presentar tu respuesta en unidades cúbicas. En el ejemplo anterior, la longitud del lado del cubo se midió en centímetros, así que el volumen se dio en centímetros cúbicos. Si la longitud del lado del cubo hubiera sido 3 cm, por ejemplo, el volumen sería V = (3 cm)3 o V = 27 cm3.Anuncio
Método 2
Método 2 de 6:Calcular el volumen de un sólido rectangular
-
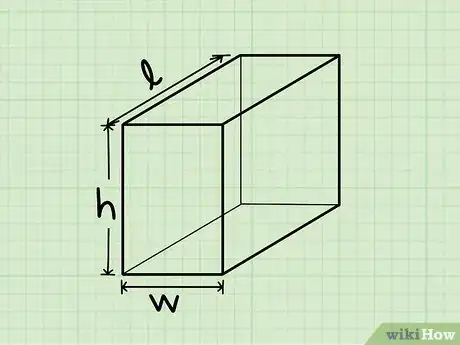
1Reconoce un sólido rectangular. Un sólido rectangular, también conocido como un prisma regular, es una forma tridimensional con seis lados rectángulos.[4] En otras palabras, un sólido rectangular es simplemente un rectángulo o forma de caja tridimensional.
- Un cubo es en realidad solo un sólido rectangular especial en el que los lados de todos los rectángulos son iguales.
-
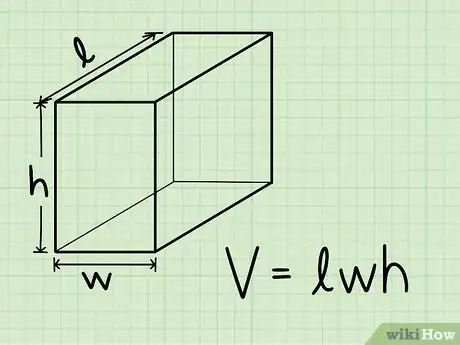
2Aprende la fórmula para calcular el volumen de un sólido rectangular. La fórmula para el volumen de un sólido rectangular es V = longitud * ancho * altura, o V = lwh.[5]
-
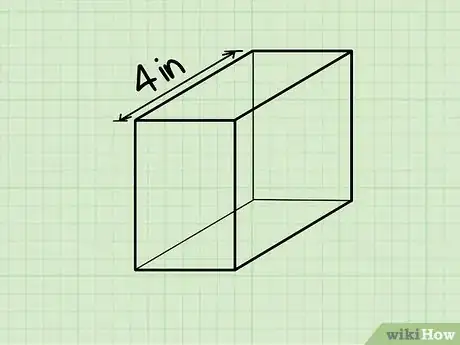
3Halla el largo del sólido rectangular. La longitud es el lado más largo del sólido rectangular que es paralelo al suelo o la superficie sobre la cual está apoyado. La longitud puede darse en un diagrama o quizás debas medirla con una regla o cinta métrica.
- Ejemplo: la longitud de este sólido rectangular es de 10 cm (4 pulgadas), así que l = 10 cm.
- No te preocupes demasiado por cuál lado es el largo; cuál, el ancho; etc. Con tal de que termines con tres medidas diferentes, el cálculo dará el mismo resultado independientemente de cómo ordenes los términos.
-
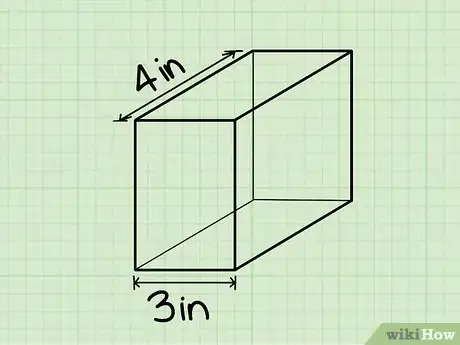
4Halla el ancho del sólido rectangular. El ancho del sólido rectangular es la medida del lado más corto del sólido que sea paralelo al suelo o la superficie sobre la cual está apoyado. Nuevamente, busca una etiqueta en el diagrama que indique el ancho o mídelo con una regla o cinta métrica.
- Ejemplo: el ancho de este sólido rectangular es de 7,5 cm (3 pulgadas), así que a = 7,5 cm.
- Si mides el sólido rectangular con una regla o cinta métrica, recuerda tomar y registrar todas las medidas en las mismas unidades. No midas un lado en pulgadas y el otro en centímetros; ¡todas las medidas deben usar la misma unidad!
-
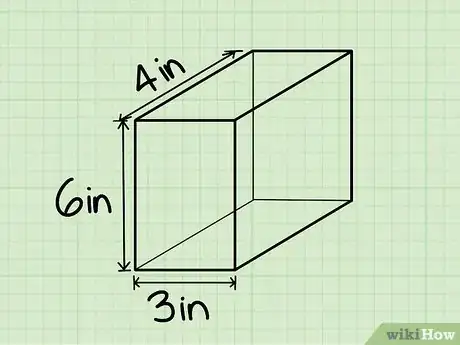
5Halla la altura del sólido rectangular. Esta altura es la distancia desde el suelo o superficie sobre la cual el sólido rectangular está apoyado hasta su parte superior. Ubica la información en tu diagrama o mide la altura usando una regla o cinta métrica.
- Ejemplo: la altura de este sólido rectangular es de 15 cm (6 pulgadas), así que h = 15 cm.
-
6Sustituye las dimensiones del sólido rectangular en la fórmula para el volumen y calcula. Recuerda que V = l x w x h.
- En nuestro ejemplo, l = 10, w = 7,5 y h = 15. Por lo tanto, V = 10 x 7,5 x 15 = 1125.
-
7Asegúrate de expresar tu respuesta en unidades cúbicas. Debido a que el sólido del ejemplo estaba medido en centímetros, el volumen debe escribirse como 1125 centímetros cúbicos o 1125 cm3 (72 pulgadas cúbicas).
- Si las medidas del sólido rectangular fueran: longitud = 2 cm, ancho = 4 cm, y altura = 8 cm, el volumen sería 2 cm x 4 cm x 8 cm, o 64 cm3.
Anuncio
Método 3
Método 3 de 6:Calcular el volumen de un cilindro
-
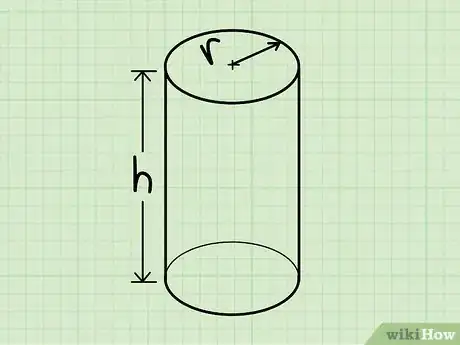
1Aprende a identificar un cilindro. Un cilindro es una forma tridimensional que tiene dos extremos planos idénticos que son circulares y un solo lado curvo que los une.[6]
- Una lata es un buen ejemplo de un cilindro, y también lo es una batería AA o AAA.
-
2Memoriza la fórmula del volumen de un cilindro. Para calcular el volumen de un cilindro, debes saber su altura y el radio de la base circular (la distancia del centro del círculo al borde) en la parte superior y la inferior. La fórmula es V = πr2h, en donde "V" es el volumen, "r" es el radio de la base circular, "h" es la altura y π es la constante pi.
- En algunos problemas de geometría, la respuesta se dará en términos de pi, pero, en la mayoría de los casos, es suficiente redondear pi a 3,14. Consulta con tu instructor para averiguar qué es lo que prefiere.
- La fórmula para hallar el volumen de un cilindro en realidad es muy similar a la utilizada para un sólido rectangular: simplemente multiplicas la altura de la figura por el área superficial de la base. En un sólido rectangular, esta área superficial es la longitud x el ancho; para el cilindro, es πr2, el área de un círculo con un radio "r".
-
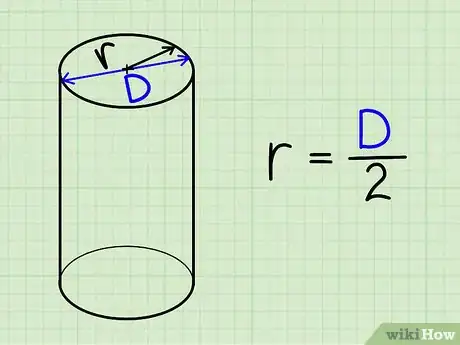
3Halla el radio de la base. Si se te da el radio en el diagrama, simplemente usa ese número. Si se te da el diámetro en lugar del radio, simplemente tienes que dividir el valor entre 2 para obtener el radio (d = 2r).
-
4Mide el objeto si no se te da el radio. Ten en cuenta que obtener medidas precisas de un sólido circular puede ser un poco complicado. Una opción es medir la base del cilindro a través de la parte superior con una regla o cinta métrica. Haz tu mejor esfuerzo para medir el cilindro en su parte más ancha y divide esta medida entre 2 para hallar el radio.
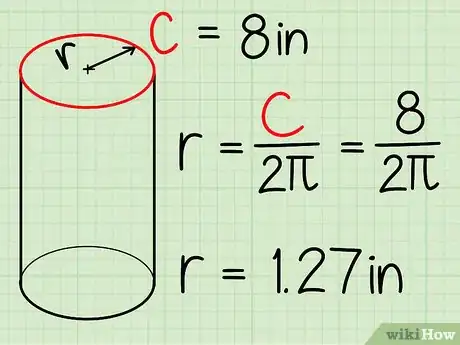
- Otra opción es medir la circunferencia del cilindro (la distancia alrededor de él) usando una cinta métrica o un trozo de cuerda que puedas marcar y luego medir con una regla. Luego, sustituye las medidas en la fórmula C (circunferencia) = 2πr. Divide la circunferencia entre 2π (6,28) y esto te dará el radio.
- Por ejemplo, si la circunferencia que mediste es de 20 cm (8 pulgadas), el radio sería 3,18 cm (1,27 pulgadas).
- Si necesitas una medida muy precisa, puedes usar ambos métodos para asegurarte de que las medidas sean similares. Si no lo son, vuelve a revisarlas. El método de la circunferencia, generalmente, produce resultados más precisos.
-
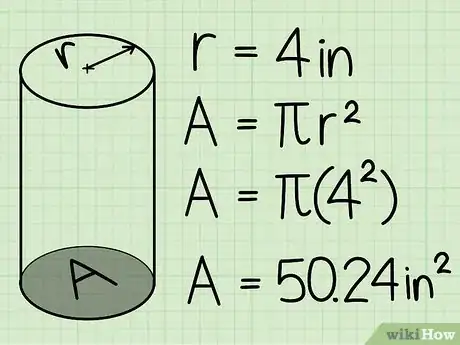
5Calcula el área de la base circular. Sustituye el radio de la base en la fórmula πr2. Luego, multiplica el radio por sí mismo una vez y luego multiplica el producto por π. Por ejemplo:
- Si el radio del círculo es igual a 10 cm (4 pulgadas), el área de la base será A = π102.
- 102 = 10 x 10, o 100. 100 x π (3,14) = 314 cm2 (50,24 pulgadas cuadradas).
- Si tienes el diámetro de la base en lugar del radio, recuerda que d = 2r. Simplemente tienes que dividir el diámetro por la mitad para hallar el radio.
-
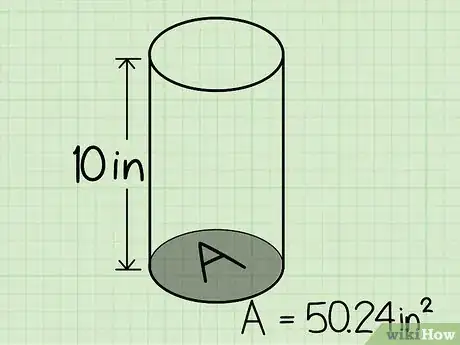
6Halla la altura del cilindro. Esto es simplemente la distancia entre las dos bases circulares o la distancia desde la superficie sobre la cual el cilindro está apoyado hasta la parte superior de este. Encuentra en tu diagrama la etiqueta que indica la altura del cilindro o mide la altura con una regla o cinta métrica.
-
7Multiplica el área de la base por la altura del cilindro para hallar el volumen. También puedes ahorrarte un paso y simplemente sustituir los valores de las dimensiones del cilindro en la fórmula V = πr2h. Para el cilindro del ejemplo con un radio de 10 cm (4 pulgadas) y una altura de 25 cm (10 pulgadas), las medidas son las siguientes:
- V = π10225
- π102 = 314
- 314 x 25 = 7850
- V = 7850
-
8Recuerda presentar tu respuesta en unidades cúbicas. El cilindro del ejemplo se midió en centímetros, así que el volumen debe expresarse en centímetros cúbicos: V = 7850 cm3. Si el cilindro se hubiera medido en pulgadas, el volumen se expresaría en pulgadas cúbicas.Anuncio
Método 4
Método 4 de 6:Calcular el volumen de una pirámide regular
-
1Comprende qué es una pirámide regular. Una pirámide regular es una forma tridimensional con un polígono como base y lados laterales que se estrechan hasta formar un vértice (la punta de la pirámide).[7] Una pirámide regular es una pirámide en la que la base es un polígono regular, lo que significa que todos los lados del polígono son de igual longitud y todos los ángulos son de igual medida.[8]
- Por lo general, nos imaginamos a una pirámide con una base cuadrada y lados que se estrechan hasta una sola punta, pero la base de una pirámide en realidad puede tener 5, 6 ¡o incluso 100 lados!
- Una pirámide con una base circular se llama cono, el cual se discutirá en el siguiente método.
-
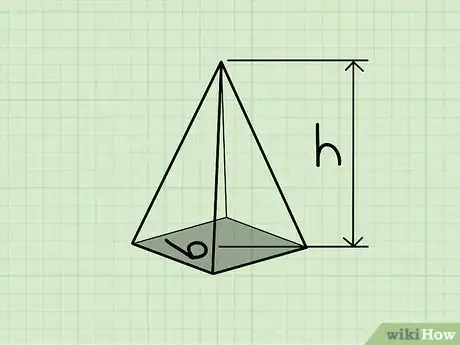
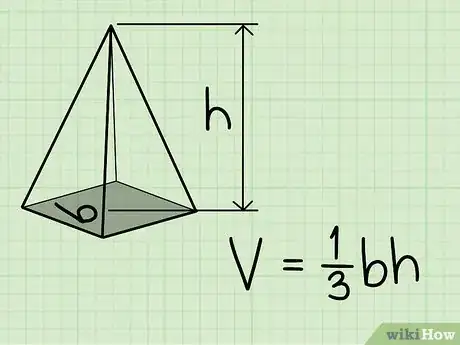
2Aprende la fórmula para el volumen de una pirámide regular. La fórmula para el volumen de una pirámide regular es V = 1/3bh, en donde "b" es el área de la base de la pirámide (el polígono en la parte inferior) y "h" es la altura de la pirámide, o la distancia vertical desde la base hasta el vértice (la punta).
- La fórmula del volumen es la misma para pirámides rectas, en las que la punta está directamente sobre el centro de la base, y para pirámides oblicuas, en las que la punta no está centrada.
-
3Calcula el área de la base. La fórmula para esto dependerá del número de lados que tenga la base de la pirámide. En la pirámide de nuestro diagrama, la base es un cuadrado con lados que tienen 15 cm (6 pulgadas) de largo. Recuerda que la fórmula para el área de un cuadrado es A = l2, en donde "l" es la longitud de los lados. Así que, para esta pirámide, el área de la base es (15)2, o 225 cm2 (36 pulgadas cuadradas).
- La fórmula del área de un triángulo es A = 1/2bh, en donde "b" es la base del triángulo y "h" es la altura.
- Es posible hallar el área de cualquier polígono regular usando la fórmula A = 1/2pa, en donde "A" es el área, "p" es el perímetro de la figura y "a" es la apotema o la distancia desde el centro de la figura hasta el punto medio de cualquiera de sus lados. Este es un cálculo bastante complicado que va más allá del ámbito de este artículo, pero dale un vistazo al artículo Cómo calcular el área de un polígono para obtener buenas instrucciones sobre cómo usar esta fórmula. También puedes facilitarte la vida y buscar una calculadora de polígonos regulares en línea.[9]
-
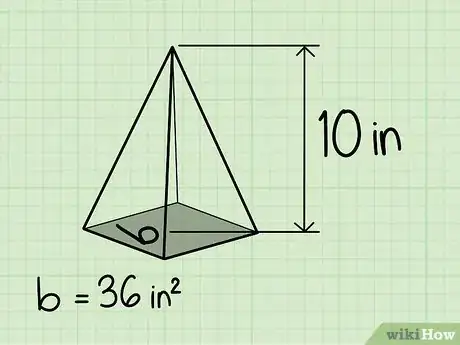
4Halla la altura de la pirámide. En la mayoría de los casos, esto se indicará en el diagrama. En nuestro ejemplo, la altura de la pirámide es de 25 cm (10 pulgadas).
-
5Multiplica el área de la base de la pirámide por su altura y divídela entre 3 para hallar el volumen. Recuerda que la fórmula para el volumen es V = 1/3bh. En la pirámide del ejemplo, la cual tenía una base con un área de 225 y una altura de 25, el volumen es: 225 x 25 x 1/3, o 1875.
- Si tuviéramos una pirámide diferente, con una base pentagonal de un área de 66 y una altura de 20, el volumen sería: 1/3 x 66 x 10 = 220.
-
6Recuerda expresar tu respuesta en unidades cúbicas. Las medidas de nuestra pirámide de ejemplo se dieron en centímetros, así que su volumen debe expresarse en centímetros cúbicos, o 1875 cm3 (120 pulgadas cúbicas). Si nuestra pirámide se hubiera medido en pulgadas, el volumen se expresaría en pulgadas cúbicas.Anuncio
Método 5
Método 5 de 6:Calcular el volumen de un cono
-
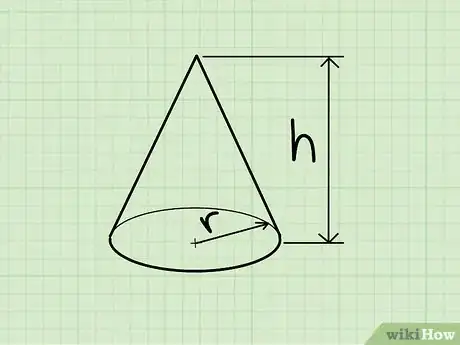
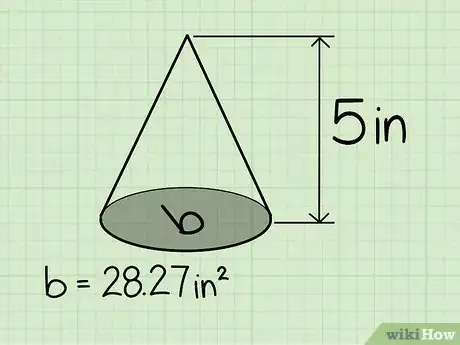
1Aprende las propiedades de un cono. Un cono es un sólido tridimensional que tiene una base circular y un solo vértice (la punta del cono). Otra forma de verlo es que un cono es una pirámide especial que tiene una base circular.[10]
- Si el vértice del cono está directamente sobre el centro de la base circular, al cono se le llama "cono recto". Si no está directamente sobre el centro, al cono se le llama "cono oblicuo". Afortunadamente, la fórmula para calcular el área de un cono es la misma ya sea recto u oblicuo.
-
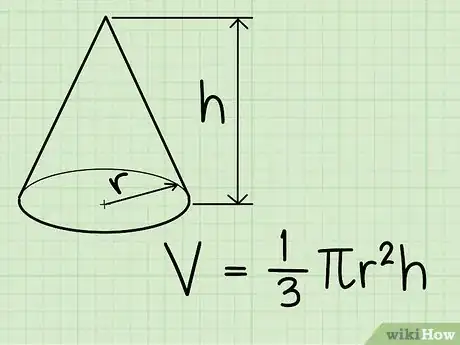
2Conoce la fórmula para calcular el volumen de un cono. La fórmula es V = 1/3πr2h, en donde "r" es el radio de la base circular del cono, "h" es la altura del cono y π es la constante pi, la cual puede redondearse a 3,14.
- La parte de πr2 de la fórmula se refiere al área de la base circular del cono. La fórmula para el volumen del cono es, por lo tanto, 1/3bh, tal como la fórmula para el volumen de una pirámide en el método anterior.
-
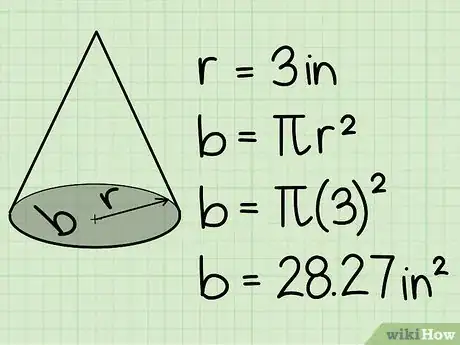
3Calcula el área de la base circular del cono. Para hacer esto, tienes que saber el radio de la base, el cual debe figurar en el diagrama. Si, en cambio, se te da el diámetro de la base circular, simplemente divide ese número entre 2, ya que el diámetro es simplemente 2 veces el radio (d = 2r). Luego, sustituye el radio en la fórmula A = πr2 para calcular el área.
- En el ejemplo del diagrama, el radio de la base circular del cono es de 7,5 cm (3 pulgadas). Cuando sustituimos esto en la fórmula, obtenemos: A = π(7,5)2.
- 7,52 = 56,25, así que A = 56,25π cm2 (9π pulgadas cuadradas).
- A = 176,62 cm2 (28,27 pulgadas cuadradas).
-
4Halla la altura del cono. Esta es la distancia vertical entre la base del cono y su vértice. En nuestro ejemplo, la altura del cono es de 12 cm (5 pulgadas).
-
5Multiplica la altura del cono por el área de la base. En nuestro ejemplo, el área de la base es 176,62 cm2 (28,27 pulgadas cuadradas) y la altura es 12 cm (5 pulgadas), así que bh = 176,62 x 12 = 2119,5 cm3 (141,35 pulgadas cúbicas).
-
6Ahora multiplica el resultado por 1/3 (o simplemente divide entre 3) para hallar el volumen del cono. En el paso anterior, en realidad calculamos el volumen del cilindro que se formaría si las paredes del cono se extendieran hacia arriba hacia otro círculo en lugar de inclinarse hacia una sola punta. Dividir entre 3 nos da el volumen solo del cono en sí.
- En nuestro ejemplo, 2119,5 x 1/3 = 706,5, el volumen de nuestro cono.
- Para reformularlo, 1/3π(7,5)2(12) = 706,5.
-
7Recuerda expresar tu respuesta en unidades cúbicas. Nuestro cono se midió en centímetros, así que su volumen debe expresarse en centímetros cúbicos: 706,5 cm3 (47,12 pulgadas cúbicas).Anuncio
Método 6
Método 6 de 6:Calcular el volumen de una esfera
-
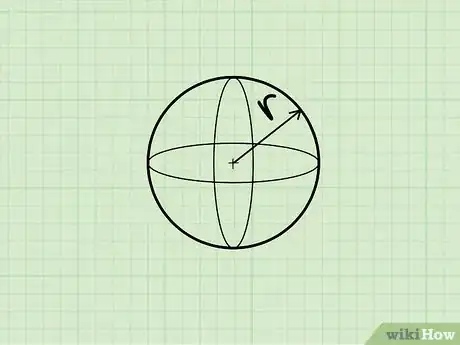
1Identifica a una esfera. Una esfera es un objeto tridimensional perfectamente redondo en el que cada punto de la superficie se encuentra a igual distancia del centro. En otras palabras, una esfera es un objeto en forma de bola.[11]
-
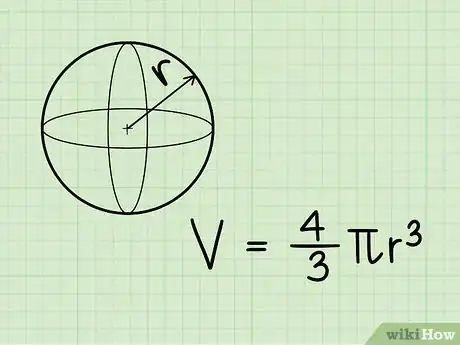
2Aprende la fórmula para el volumen de una esfera. La fórmula para el volumen de una esfera es V = 4/3πr3 (escrito: "cuatro tercios de pi por r al cubo"), en donde "r" es el radio de la esfera y π es la constante pi (3,14).[12]
-
3Halla el radio de la esfera. Si tienes el radio en el diagrama, hallar "r" es solo será cuestión de localizarlo. Si se te da el diámetro, debes dividir este número entre 2 para hallar el radio. Por ejemplo, el radio de la esfera en el diagrama es de 7,5 cm (3 pulgadas).
-
4Mide la esfera si no se te da el radio. Si necesitas medir un objeto esférico (como una pelota de tenis) para hallar el radio, primero busca un trozo de cuerda lo suficientemente largo como para envolverlo alrededor del objeto. Luego, envuelve la cuerda alrededor del objeto en su punto más ancho y marca los puntos en donde la cuerda se superponga a sí misma. Luego, mide la cuerda con una regla para hallar la circunferencia. Divide ese valor entre 2π, o 6,28, y esto te dará el radio de la esfera.
- Por ejemplo, si mides una pelota y encuentras que su circunferencia es de 45 cm (18 pulgadas), divide ese número entre 6,28 y descubrirás que el radio es de 7,17 cm (2,87 pulgadas).
- Medir un objeto esférico puede ser un poco complicado, así que es posible que quieras tomar 3 medidas diferentes y luego promediarlas (sumar las tres medidas y luego dividir entre 3) para asegurarte de tener el valor más preciso posible.
- Por ejemplo, si tus tres medidas para la circunferencia fueron 45 cm (18 pulgadas), 45,08 cm (17,75 pulgadas) y 46,2 cm (18,2 pulgadas), sumarías esos tres valores (45 + 45,08 + 46,2 = 136,28 cm o 53,95 pulgadas) y dividirías ese valor entre 3 (136,28/3 = 45,43 cm o 17,98 pulgadas). Usa este valor promedio en los cálculos del volumen.
-
5Eleva el radio al cubo para hallar r3. Elevar un número al cubo simplemente significa multiplicar el número por sí mismo 2 veces, así que r3 = r x r x r. En nuestro ejemplo, r = 7,5, así que r3 = 7,5 x 7,5 x 7,5, o 421,88.
-
6Ahora multiplica tu respuesta por 4/3. Puedes ya sea usar tu calculadora o hacer la multiplicación a mano y luego simplificar la fracción. En nuestro ejemplo, multiplicar 421,88 por 4/3 = 1687,5/3 o 562,5.
-
7Multiplica el resultado por π para hallar el volumen de la esfera. El último paso para calcular el volumen es simplemente multiplicar el resultado que tienes hasta el momento por π. Redondear π a dos dígitos generalmente es suficiente para la mayoría de problemas de matemáticas (a menos que tu profesor haya especificado lo contrario), así que multiplica por 3,14 y tendrás tu respuesta.
- En nuestro ejemplo, 562,5 x 3,14 = 1766,25.
-
8Expresa tu respuesta en unidades cúbicas. En nuestro ejemplo, la medida del radio de la esfera estaba en centímetros, así que nuestra respuesta en realidad es V = 1766,25 centímetros cúbicos (1766,25 cm3 o 113,09 pulgadas cúbicas).Anuncio
Referencias
- ↑ http://www.mathsisfun.com/definitions/volume.html
- ↑ http://www.mathsisfun.com/measure/us-standard-volume.html
- ↑ https://www.mathsisfun.com/definitions/cube.html
- ↑ http://www.algebralab.org/lessons/lesson.aspx?file=Geometry_3Dprisms.xml
- ↑ http://www.studyzone.org/mtestprep/math8/g/rectvolumel.cfm
- ↑ https://www.mathsisfun.com/definitions/cylinder.html
- ↑ http://www.mathwords.com/p/pyramid.htm
- ↑ http://www.mathwords.com/r/regular_pyramid.htm
- ↑ http://www.calculatorsoup.com/calculators/geometry-plane/polygon.php
Acerca de este wikiHow
Para calcular el volumen de un cubo, utiliza la fórmula v = s^3, donde s es la longitud de los lados del cubo. Para calcular el volumen de un cilindro, utiliza la fórmula v = hπr^2, donde r es el radio de la base, h la altura y π el número pi. Si necesitas calcular el volumen de un prisma rectangular, utiliza la fórmula v = lwh, donde l es la longitud, w el ancho y h la altura.




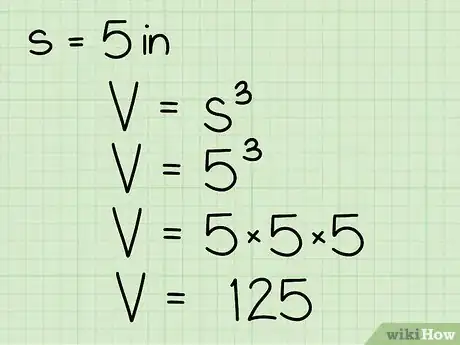
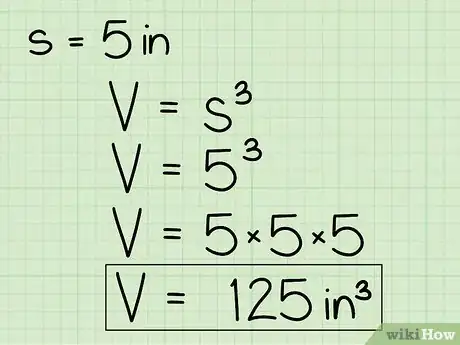
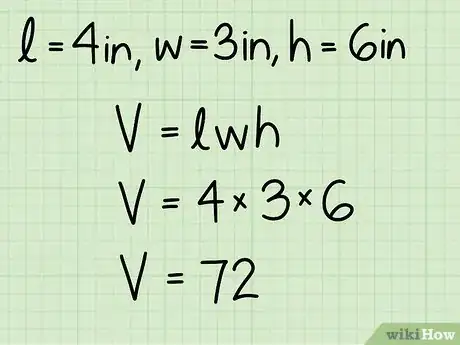
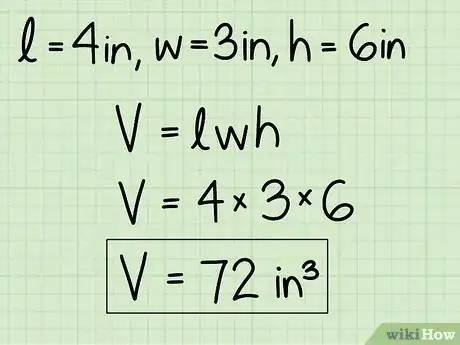
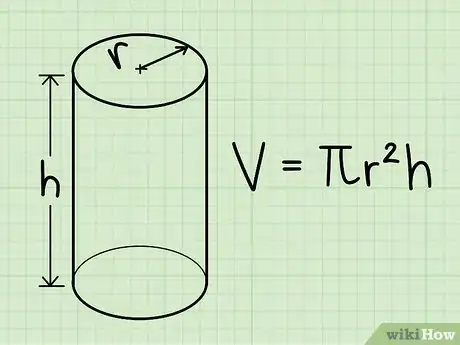


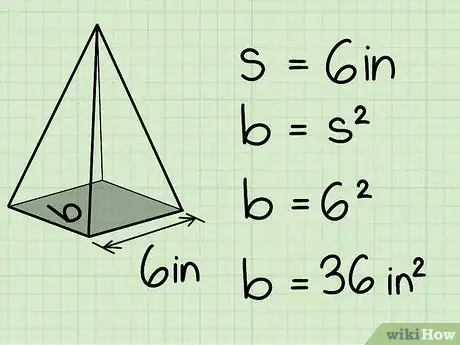
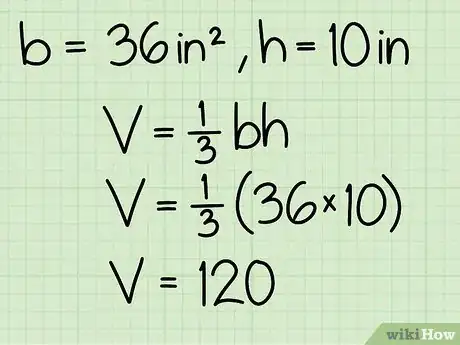
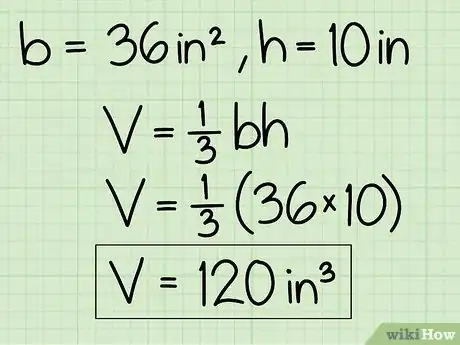
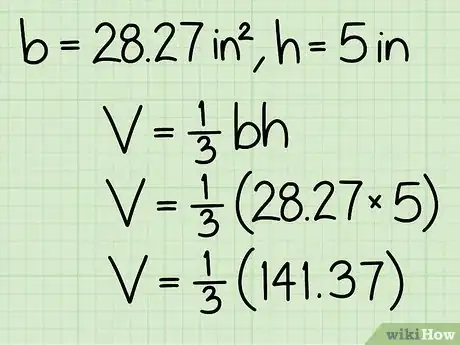


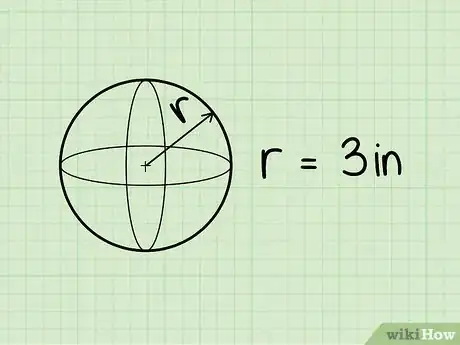

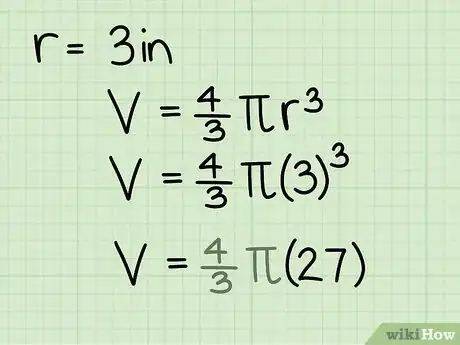









-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)