wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 49 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 490 902 veces.
¿Cómo cambias esos números y letras extraños en algo que tú o tu computadora puedan entender? Convertir un número hexadecimal en un número binario es muy fácil y es por eso que el sistema hexadecimal se ha adaptado en algunos lenguajes de programación. Realizar una conversión al sistema decimal es un poco más complicado, pero una vez que lo entiendas, será fácil repetir el proceso para cualquier número.
Pasos
Parte 1
Parte 1 de 3:Convertir un número hexadecimal a uno binario
-
1Convierte cada dígito hexadecimal a cuatro dígitos binarios. El sistema hexadecimal se adoptó en primer lugar debido a lo sencillo que es realizar conversiones ambos. Básicamente, el sistema hexadecimal se utiliza como una forma de mostrar la información binaria en una cadena más corta.[1] Este gráfico es lo único que necesitarás para convertir un número a otro:
Hexadecimal Binario 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 A 1010 B 1011 C 1100 D 1101 E 1110 F 1111 -
2Hazlo tú mismo. Es en verdad tan simple como cambiar el dígito en cuatro dígitos binarios equivalentes. Los siguientes son algunos números hexadecimales que puedes convertir. Resalta el texto invisible a la derecha del signo igual para verificar tu respuesta:
- A23 = 1010 0010 0011
- BEE = 1011 1110 1110
- 70C558 = 0111 0000 1100 0101 0101 1000
-
3Entiende la razón por la que funciona. En el sistema binario con "base dos", pueden utilizarse n dígitos binarios para representar 2n números diferentes. Por ejemplo, con cuatro dígitos binarios, puedes representar 24 = 16 números diferentes. Dado que el hexadecimal es un sistema con base de dieciséis, se puede utilizar un dígito para representar 161 = 16 números diferentes. Esto hace que la conversión entre ambos sistemas sea sumamente sencilla.
- También puedes verlo como si los sistemas de conteo "se dieran vuelta" a otro dígito al mismo tiempo. El sistema hexadecimal cuenta "...D, E, F, 10" al mismo tiempo que el binario cuenta "1101, 1110, 1111, 10000".
Parte 2
Parte 2 de 3:Convertir un número hexadecimal a uno decimal
-
1Verifica la forma en la que funciona la base diez. Puedes utilizar la notación decimal a diario sin detenerte a pensar en el significado, pero cuando lo aprendiste por primera vez, es posible que tu padre o tu maestro te lo hayan explicado con más detalle. Una revisión rápida de la manera en que los números ordinarios se escriben te ayudará a convertir dicho número:
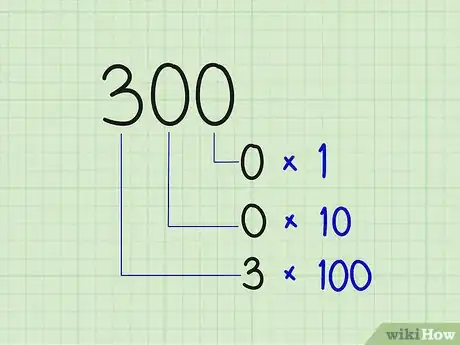
- Cada dígito en un número decimal se encuentra en un "lugar" determinado. Si nos movemos de derecha a izquierda, encontraremos el "lugar de las unidades", "el de las decenas", "el de las centenas", etc. El dígito 3 simplemente significará 3 si se le coloca en el lugar de las unidades, pero representará 30 si se ubica en el de las decenas y 300 en el de las centenas.
- Para ponerlo en términos matemáticos, los "lugares" representan 100, 101, 102 y así sucesivamente. Esta es la razón por la que este sistema se llama "base diez" o "decimal" en nombre a la palabra latina para "décimo".
-
2Escribe un número decimal como un problema de suma. Tal vez parezca obvio, pero es el mismo proceso que emplearemos para convertir un número hexadecimal, así que es un buen punto de partida. Escribamos el número 480,13710. Recuerda que el subíndice 10 nos indica que el número está escrito en una base diez:
- Comienza con el dígito en el extremo derecho, 7 = 7 x 100 o 7 x 1
- Luego ve hacia la izquierda, 3 = 3 x 101 o 3 x 10
- Al repetir todos los dígitos, resolvemos que 480,137 = 4x100,000 + 8x10,000 + 0x1,000 + 1x100 + 3x10 + 7x1.
-
3Escribe los valores de lugar al lado de un número hexadecimal. Dado que el sistema hexadecimal tiene base dieciséis, los "valores de lugar" corresponden a potencias de dieciséis. Para realizar la conversión al sistema decimal, multiplica cada valor de lugar por la potencia de dieciséis respectiva. Comienza este proceso escribiendo las potencias de dieciséis al lado de los dígitos de un número hexadecimal. Utilizaremos como ejemplo el número hexadecimal C92116. Comienza a la derecha con 160 y aumenta el exponente cada vez que pases al siguiente dígito de la izquierda:
- 116 = 1 x 160 = 1 x 1 (todos los números tienen valor decimal salvo donde se indica)
- 216 = 2 x 161 = 2 x 16
- 916 = 9 x 162 = 9 x 256
- C = C x 163 = C x 4096
-
4Convierte caracteres alfabéticos al sistema decimal. Los dígitos numéricos son los mismos tanto en el sistema decimal como en el hexadecimal, así que no necesitarás cambiarlos (por ejemplo, 716 = 710). En el caso de caracteres alfabéticos, consulta la siguiente lista para cambiarlos a un equivalente decimal:
- A = 10
- B = 11
- C = 12 (lo utilizaremos en nuestro ejemplo anterior)
- D = 13
- E = 14
- F = 15
-
5Realiza el cálculo. Ahora que todo está escrito en números decimales, resuelve cada problema de multiplicación y suma los resultados. Una calculadora será muy útil para la mayoría de los números hexadecimal. Siguiendo con el ejemplo anterior, aquí C921 se vuelve a escribir como una fórmula decimal y se resuelve:
- C92116 = (en decimal) (1 x 1) + (2 x 16) + (9 x 256) + (12 x 4096)
- = 1 + 32 + 2,304 + 49,152.
- = 51,48910. Por lo general, la versión decimal tendrá más dígitos que la hexadecimal, pues esta última puede almacenar más información por dígito.
-
6Practica la conversión. Estos son algunos números que puedes convertir del sistema hexadecimal al decimal. Una vez que tengas la respuesta, resalta el texto invisible a la derecha del signo igual para verificarla:
- 3AB16 = 93910
- A1A116 = 4137710
- 500016 = 2048010
- 500D16 = 2049310
- 18A2F16 = 10091110
Parte 3
Parte 3 de 3:Comprender los aspectos básicos del sistema hexadecimal
-
1Aprende a usar el sistema hexadecimal. Nuestro sistema decimal regular tiene como base a las decenas, utilizando diez símbolos diferentes para mostrar los números. El hexadecimal es un sistema que tiene como base el dieciséis, lo que significa que emplea dieciséis caracteres para mostrar los números.
- Comenzando desde el cero en adelante:
Hexadecimal Decimal Hexadecimal Decimal 0 0 10 16 1 1 11 17 2 2 12 18 3 3 13 19 4 4 14 20 5 5 15 21 6 6 16 22 7 7 17 23 8 8 18 24 9 9 19 25 A 10 1A 26 B 11 1B 27 C 12 1C 28 D 13 1D 29 E 14 1E 30 F 15 1F 31
- Comenzando desde el cero en adelante:
-
2Utiliza un subíndice para mostrar qué sistema utilizas. Cada vez que pueda parecer poco claro el sistema que utilizas, emplea un número decimal en el subíndice para denotar la base. Por ejemplo, 1710 significa "diecisiete con base diez" (un número decimal cualquiera). 1710 = 1116 u "11 con base de dieciséis" (hexadecimal). Puedes omitirlo si tu número hexadecimal contiene un caracter alfabético, como B o E. Nadie lo confundirá con un número decimal.
Consejos
- Podría ser necesario utilizar una calculadora en línea para convertir los números hexadecimales grandes a decimales. También puedes ahorrarte el trabajo y utilizar un conversor en línea para que haga el trabajo por ti, aunque es recomendable saber cómo funciona el proceso.[2]
- Puedes adaptar la conversión "hexadecimal a decimal" para convertir cualquier otro sistema de numeración con base x al sistema decimal. Simplemente reemplaza las potencias de dieciséis con las de x. ¡Trata de aprender el sistema de numeración babilónica con base 60![3]









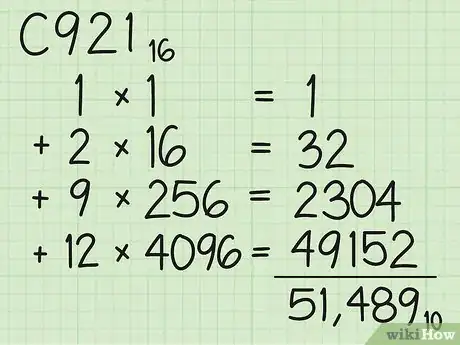









-to-Grams-(g)-Step-9-Version-4.webp)
-to-Fahrenheit-(°F)-Step-6.webp)