Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 8 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 256 031 veces.
Existe una gran cantidad de formas de hallar la dimensión faltante de un rectángulo, y el método que utilices dependerá de la información que ya tengas. Ten en cuenta que puedes hacerlo siempre y cuando conozcas el área o perímetro de la figura y la longitud de uno de los lados (o la relación entre la longitud y el ancho). Las propiedades de un rectángulo te permiten emplear estos métodos para hallar la longitud o el ancho.
Pasos
Método 1
Método 1 de 4:Utilizar el área y la longitud
-
1Utiliza la fórmula para hallar el área de un rectángulo. La fórmula es , donde es el área del rectángulo, representa la longitud y , el ancho.[1]
- Este método solo funcionará si conoces el área y la longitud de uno de los lados del rectángulo.
- La fórmula también puede presentarse como , donde es la altura del rectángulo y se utiliza en lugar de la longitud.[2] Estos dos términos se refieren a la misma dimensión.
-
2Reemplaza los valores del área y la longitud en la fórmula. Asegúrate de sustituir cada variable con el valor correcto.
- Por ejemplo, si quieres hallar el ancho de un rectángulo con un área de 24 centímetros cuadrados y cuya longitud mide 8 centímetros, la fórmula deberá ser la siguiente:
- Por ejemplo, si quieres hallar el ancho de un rectángulo con un área de 24 centímetros cuadrados y cuya longitud mide 8 centímetros, la fórmula deberá ser la siguiente:
-
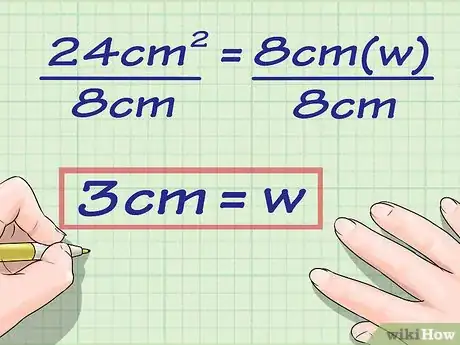
3Resuelve la ecuación para hallar . Para hacerlo, divide cada lado de la ecuación entre la longitud.
- Por ejemplo, en la ecuación , podrías dividir cada lado entre 8.
- Por ejemplo, en la ecuación , podrías dividir cada lado entre 8.
-
4Escribe tu respuesta final. No olvides colocar la unidad de medida.
- Por ejemplo, para un rectángulo con un área de y cuya longitud mide , el ancho será .
Anuncio
Método 2
Método 2 de 4:Utilizar el perímetro y la longitud
-
1Utiliza la fórmula para hallar el perímetro de un rectángulo. La fórmula es , donde es el perímetro del rectángulo, representa la longitud y , el ancho.[3]
- Este método solo funcionará si conoces el perímetro y la longitud de uno de los lados del rectángulo.
- La fórmula también puede presentarse como , donde representa la altura del rectángulo y se utiliza en lugar de la longitud.[4] Las variables y se refieren a la misma medida y, de acuerdo a la propiedad distributiva, ambas fórmulas, aunque estén redactadas de manera distinta, darán el mismo resultado.
-
2Reemplaza los valores del perímetro y la longitud en la fórmula. Asegúrate de sustituir las variables con los valores correctos.
- Por ejemplo, si quieres hallar el ancho de un rectángulo con un perímetro de 22 centímetros cuya longitud es de 8 centímetros, la fórmula será la siguiente:
- Por ejemplo, si quieres hallar el ancho de un rectángulo con un perímetro de 22 centímetros cuya longitud es de 8 centímetros, la fórmula será la siguiente:
-
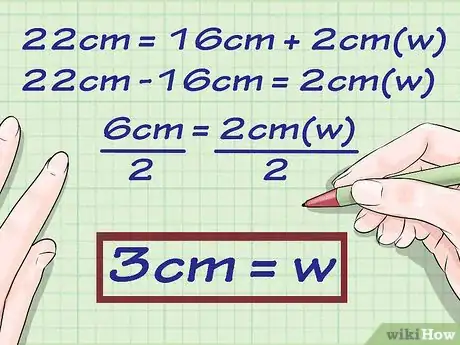
3Resuelve la ecuación para hallar . Para hacerlo, tendrás que restar la longitud a cada lado de la ecuación y luego dividir las expresiones entre 2.
- Por ejemplo, en la ecuación , tendrías que restar 16 a cada lado y luego dividir el resultado entre 2.
- Por ejemplo, en la ecuación , tendrías que restar 16 a cada lado y luego dividir el resultado entre 2.
-
4Escribe la respuesta final. No olvides incluir la unidad de medida.
- Por ejemplo, para un rectángulo con un perímetro de y cuya longitud mide , el ancho será .
Anuncio
Método 3
Método 3 de 4:Utilizar la diagonal y la longitud
-
1Utiliza la fórmula para hallar la diagonal de un rectángulo. La fórmula es , donde es la medida de la diagonal del rectángulo, representa la longitud y , el ancho.[5]
- Este método solo funcionará si conoces la medida de la diagonal y la longitud de uno de los lados del rectángulo.
- La fórmula también puede presentarse como , donde es la altura del rectángulo y se utiliza en lugar de la longitud.[6] Las variables y se refieren a la misma medida.
-
2Reemplaza los valores de la diagonal y la altura en la fórmula. Asegúrate de sustituir las variables con los valores correctos.
- Por ejemplo, si quieres hallar el ancho de un rectángulo con una diagonal de 5 centímetros y cuya altura mide 4 centímetros, la fórmula será la siguiente:
-
3Eleva al cuadrado ambos lados de la ecuación. Tendrás que eliminar la raíz cuadrada a fin de que sea más sencillo aislar la variable.
- Por ejemplo:
- Por ejemplo:
-
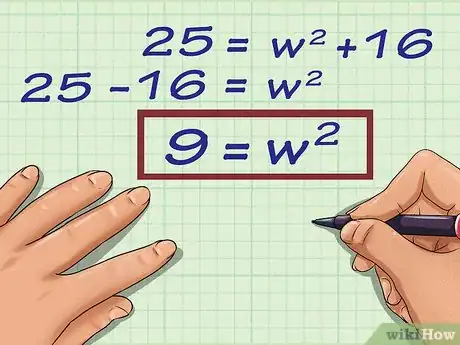
4Aísla la variable . Para hacerlo, tendrás que restar el valor de la altura al cuadrado a cada lado de la ecuación.
- Por ejemplo, en la ecuación , tendrías que restar 16 a cada lado.
- Por ejemplo, en la ecuación , tendrías que restar 16 a cada lado.
-
5Resuelve la ecuación para hallar . Para hacerlo, tendrás que calcular la raíz cuadrada a cada lado de la ecuación.
- Por ejemplo:
- Por ejemplo:
-
6Escribe la respuesta final. No olvides incluir la unidad de medida.
- Por ejemplo, para un rectángulo con una diagonal de y cuya altura mide , el ancho será .
Anuncio
Método 4
Método 4 de 4:Utilizar el área o perímetro y la longitud relativa
-
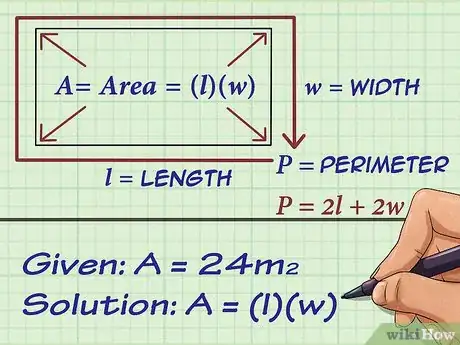
1Utiliza la fórmula para hallar el área o el perímetro de un rectángulo. La fórmula que elijas dependerá de la información que ya conozcas. Es decir, si conoces el área, utiliza la fórmula del área; si conoces el perímetro, utiliza su fórmula.
- Si no conoces ni el área ni el perímetro, o la relación entre la longitud y el ancho, no podrás aplicar este método.
- La fórmula para hallar el área de un rectángulo es .
- La fórmula para hallar el perímetro de un rectángulo es .
- Por ejemplo, quizá sepas que el área del rectángulo es 24 centímetros cuadrados. En este caso, tendrás que emplear la fórmula del área.
-
2Escribe la expresión de modo tal que describa la relación entre la longitud y el ancho. Procura que la ecuación indique el valor de .
- Dicha relación puede expresarse diciendo cuántas veces más grande es un lado que el otro o cuántas unidades más que un lado mide el otro.
- Por ejemplo, quizá sepas que la longitud del rectángulo mide 5 centímetros más que el ancho. En ese caso, la ecuación para indicar el valor de la longitud sería .
-
3Reemplaza la variable en la fórmula correspondiente con la expresión del valor de la longitud. Al hacerlo, la ecuación solo tendrá la variable , lo que significa que puedes resolverla para hallar el valor del ancho.
- Por ejemplo, si sabes que el área es 24 centímetros cuadrados y que , la fórmula se verá así:
- Por ejemplo, si sabes que el área es 24 centímetros cuadrados y que , la fórmula se verá así:
-
4Simplifica la ecuación. La ecuación simplificada puede tener varias formas según la relación entre la longitud y el ancho, y dependiendo de si trabajas con la fórmula del área o la del perímetro.[7] Considera la posibilidad de utilizar la ecuación que te permita hallar el valor de de la forma más sencilla.[
- Por ejemplo, puedes tomar la ecuación y convertirla en para simplificarla.
-
5Resuelve la ecuación para hallar el valor de . Al igual que en el paso anterior, la forma como lo hagas dependerá de la ecuación simplificada. Aplica las reglas básicas de álgebra y geometría para resolver el problema.
- Para resolver la ecuación, quizá necesites utilizar sumas o divisiones, factorizar una ecuación cuadrática, o aplicar la fórmula cuadrática.[8]
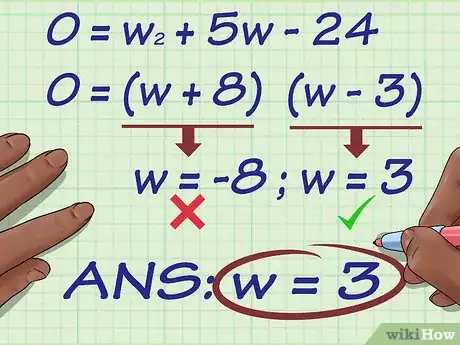
- Por ejemplo, puede factorizarse de la siguiente manera:
Por lo tanto, tendrás dos posibles soluciones para el valor de : o . Dado que la medida de las dimensiones de un rectángulo no puede ser negativa, simplemente eliminarás -8. Por lo tanto, la solución es .[9]
Anuncio
Referencias
- ↑ http://www.coolmath.com/reference/rectangles# The_area_of_a_rectangle
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.virtualnerd.com/middle-math/geometry-measurement/rectangle-perimeter-area/rectangle-perimeter-example
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://www.coolmath.com/reference/rectangles# The_diagonal_of_a_rectangle
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml











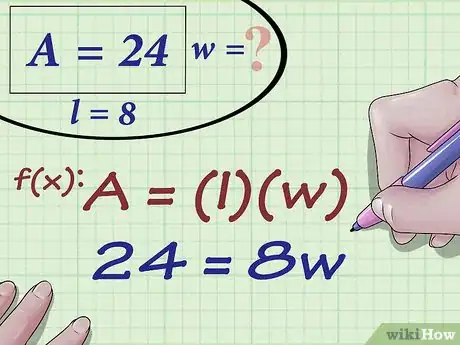













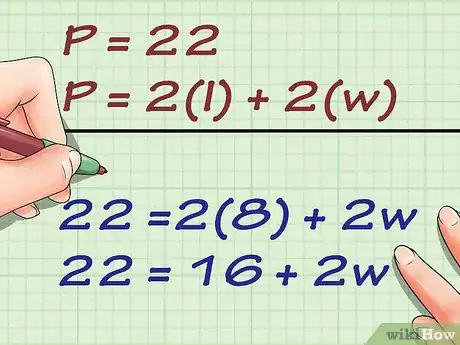


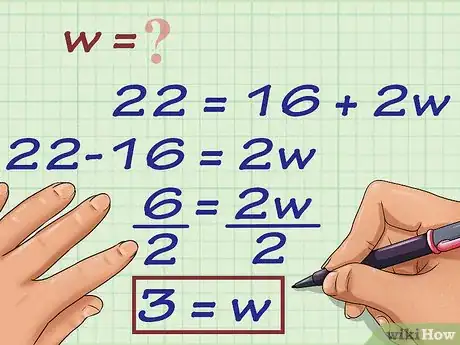



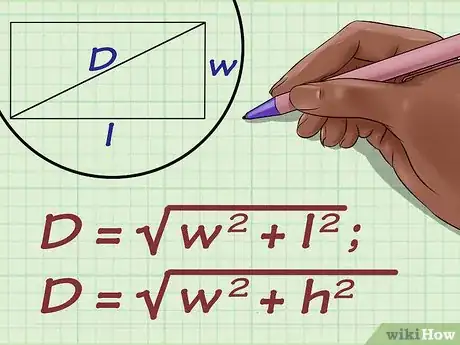



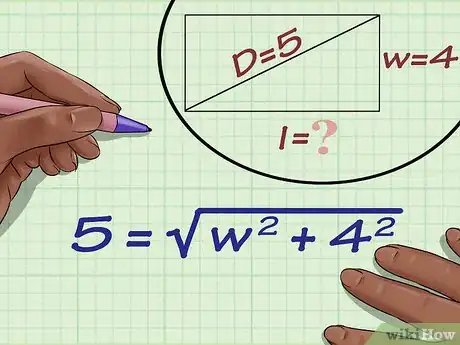

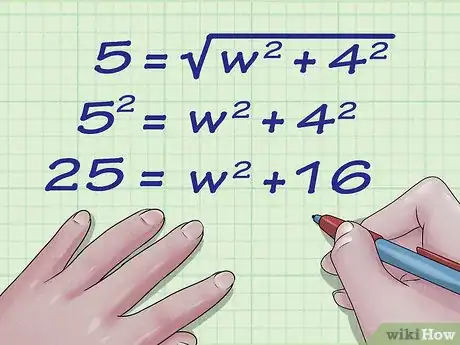




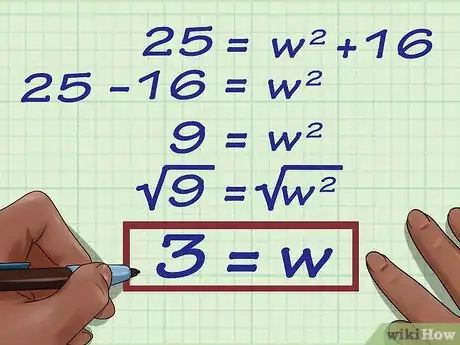






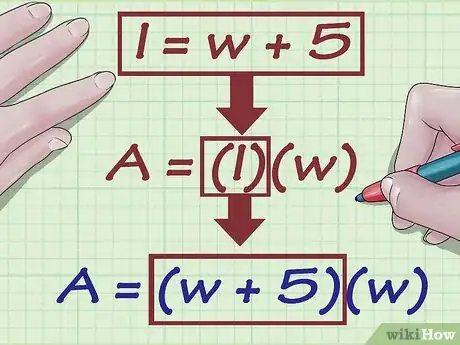













-to-Grams-(g)-Step-9-Version-4.webp)

-to-Fahrenheit-(°F)-Step-6.webp)






wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 256 031 veces.