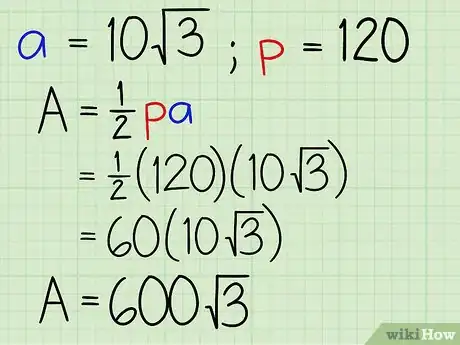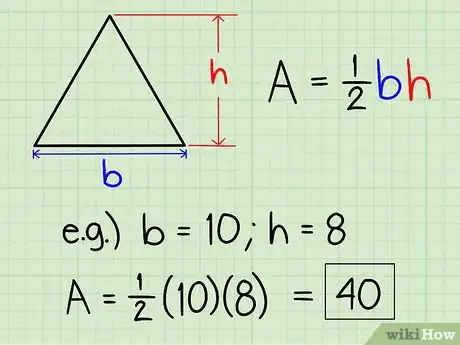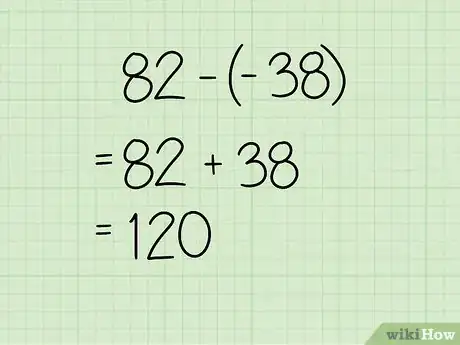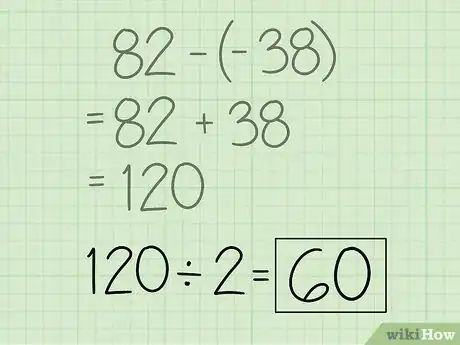Cómo calcular el área de un polígono

Información del autor

Calcular el área de un polígono puede ser tan simple como hallar el área de un triángulo regular o puede ser tan complicado como hallar el área de una figura plana irregular de once lados. Si quieres saber cómo hallar el área de distintos tipos de polígonos, solo tienes que seguir estos pasos.

Parte 1

Parte 1 de 3:
Hallar el área de un polígono regular utilizando sus apotemas

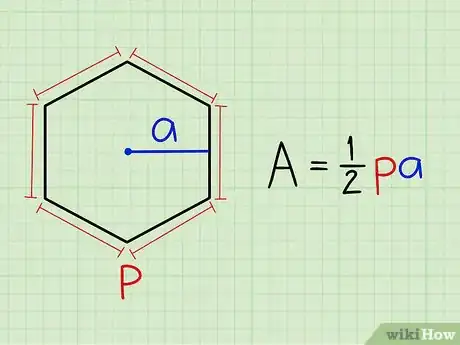
1
Anota la fórmula para hallar el área de un polígono regular. Para hallar el área de un polígono regular, lo único que tienes que hacer es seguir esta fórmula sencilla: área = 1/2 x perímetro x apotema. Aquí tienes el significado de cada elemento:
- Perímetro = la suma de las longitudes de todos los lados
- Apotema = un segmento que une el centro del polígono con el punto medio de cualquier lado perpendicular a dicho lado
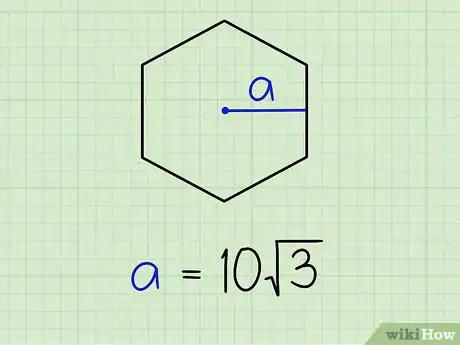
2
Halla la apotema del polígono. Si vas a utilizar el método del apotema, la longitud del apotema se dará a conocer en el problema. Imaginemos que quieres calcular el área de un hexágono cuyo apotema tiene una longitud de 10√3.
3
Halla el perímetro del polígono. Si el perímetro se da a conocer en el problema, prácticamente está todo hecho, pero es probable que haya algo más de trabajo que hacer. Si el apotema se da a conocer y sabes que se trata de un polígono regular, puedes utilizar este dato para hallar el perímetro. A continuación, verás la forma de hacerlo:
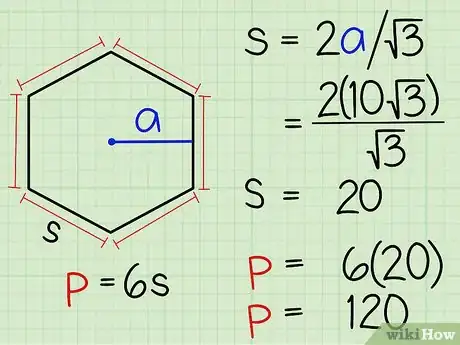
- Piensa en el apotema como si fuese el lado de longitud "x√3" perteneciente a un triángulo de 30-60-90 grados. Puedes recurrir a esta imagen porque el hexágono está formado por seis triángulos equiláteros. Cada apotema corta a uno de esos triángulos por la mitad, creando dos triángulos con ángulos de 30-60-90 grados.
- Sabes que el lado opuesto al ángulo de 60 = x√3 (el apotema), el lado opuesto al ángulo de 30 = x, y el lado opuesto al ángulo de 90 = 2x. Si 10√3 corresponde a "x√3", es fácil ver que x = 10.
- Sabes que x = la mitad de la longitud de la base del triángulo equilátero. Multiplícalo por dos para hallar la longitud total de la base. La base del triángulo tiene una longitud de 20 unidades. Hay seis de estos lados en el hexágono, así que tendrás que multiplicar 20 x 6 para obtener el perímetro del hexágono; es decir, 120.
4
Introduce en la fórmula los valores del apotema y del perímetro. Si utilizas la fórmula área = 1/2 x perímetro x apotema, puedes introducir los valores 120 unidades para el perímetro y 10√3 para el apotema. Aquí puedes ver la resolución después de añadir los valores numéricos a la fórmula:
- Área = 1/2 x 120 x 10√3
- Área = 60 x 10√3
- Área = 600√3
5
Simplifica el resultado. Es posible que debas expresar el resultado en decimales en lugar de utilizar la raíz cuadrada. Si es así, solo necesitas utilizar la calculadora para hallar el valor más aproximado a √3 y multiplicarlo por 600. √3 x 600 = 1039,2. Este es el resultado final.

Anuncio

Parte 2

Parte 2 de 3:
Hallar el área de un polígono regular utilizando otras fórmulas

1
Halla el área de un triángulo rectángulo. Si quieres hallar el área de un triángulo rectángulo, lo único que tienes que hacer es utilizar esta fórmula: área = 1/2 x base x altura.
- Si se trata de un triángulo con una base de 10 unidades y una altura de 8, el área = 1/2 x 8 x 10, o 40.
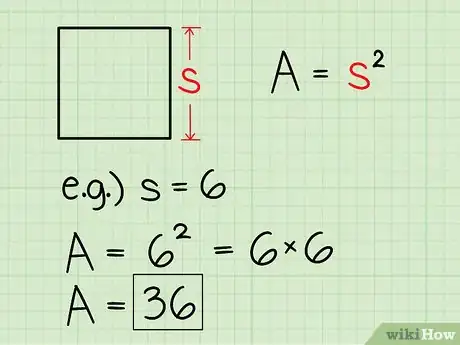
2
Halla el área de un cuadrado. Para hallar el área de un cuadrado, simplemente tienes que elevar al cuadrado la longitud de cualquiera de sus lados. Esto en realidad es lo mismo que multiplicar la base por la altura del cuadrado, ya que en el caso de esta figura en particular, la longitud de la base es igual a la de la altura.
- Si el lado del cuadrado tiene una longitud de 6 unidades, el área es 6 x 6, o 36.
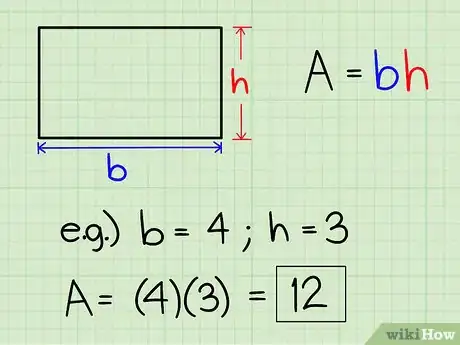
3
Halla el área de un rectángulo. Para hallar el área de un rectángulo, solo tienes que multiplicar la base por la altura.
- Si la base del rectángulo mide 4 unidades de longitud y la altura es de 3, el área es 4 x 3, o 12.
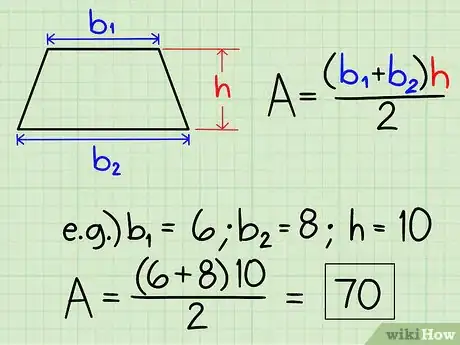
4
Halla el área de un trapezoide. Para hallar el área de un trapezoide, solo tienes que utilizar esta fórmula: área = [(base 1 + base 2) x altura]/2.
- Supongamos que tienes un trapezoide con bases de 6 y de 8 unidades de longitud, y con una altura de 10 unidades. Hallar el área es muy sencillo: [(6 + 8) x 10]/2, lo que puede simplificarse a (14 x 10)/2, o 140/2, obteniendo como resultado un área de 70.
Anuncio

Parte 3

Parte 3 de 3:
Hallar el área de un polígono irregular

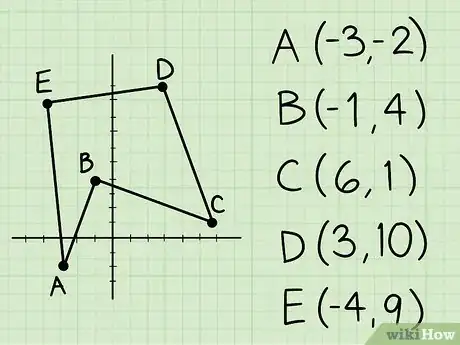
1
Anota las coordenadas de los vértices del polígono irregular. Se puede hallar el área de un polígono irregular conociendo las coordenadas de sus vértices.
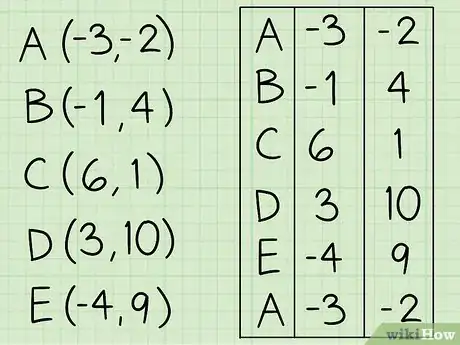
2
Haz un vector. Escribe las coordenadas “x” e “y” de cada vértice del polígono en sentido antihorario. Repite las coordenadas del primer punto al final de la lista.
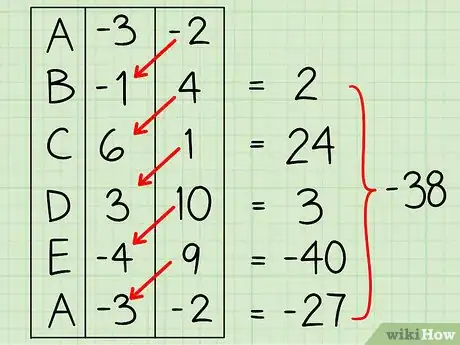
3
Multiplica la coordenada “x” de cada vértice por la coordenada “y” del siguiente vértice. Suma los resultados. La suma total de estos productos será igual a 82.
4
Multiplica la coordenada “y” de cada vértice por la coordenada “x” del siguiente vértice. De nuevo, suma estos resultados. La suma total de estos productos es igual a -38.
5
Resta el resultado de la suma de los primeros productos al resultado de la suma de los segundos productos. Resuelve restando -38 a 82: 82 - (-38) = 120.
6
Divide el resultado de esta resta entre 2 para hallar el área del polígono. Solo tienes que dividir 120 entre 2, obteniendo 60, y habrás terminado.

Anuncio

Consejos

Si anotas las coordenadas de los vértices en sentido horario en lugar de antihorario, obtendrás el resultado negativo del área. Por lo tanto, puedes utilizar este orden a la hora de anotar los vértices para identificar el patrón cíclico de una secuencia de puntos dados que forman un polígono.
Con esta fórmula, obtendrás el área con una orientación determinada. Si la utilizas para calcular el área de una figura en la que dos de los segmentos se cruzan, como las líneas de un ocho, obtendrás el área encerrada entre los puntos que siguen un sentido antihorario menos el área encerrada entre los puntos que siguen un sentido horario.

Anuncio