Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
Este artículo ha sido visto 56 191 veces.
El área es la medida de la superficie que hay en el interior de una medida bidimensional. A veces, hallar el área es tan sencillo como multiplicar dos números, pero en otras ocasiones puede ser más complicado. Este artículo te mostrará el método resumido para calcular el área de las siguientes figuras: cuadriláteros, triángulos, círculos, la superficie de una pirámide o un cilindro, y el área que hay bajo un arco.
Pasos
Método 1
Método 1 de 10:Rectángulos
-
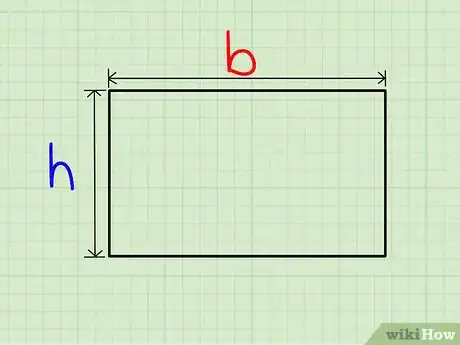
1Halla las longitudes de dos lados consecutivos del rectángulo. Dado que los rectángulos están compuestos por dos pares de lados opuestos y de igual longitud, consideraremos un lado como la base (b) y otro como la altura (h). Generalmente, el lado horizontal es la base y el vertical, la altura.[1]
-
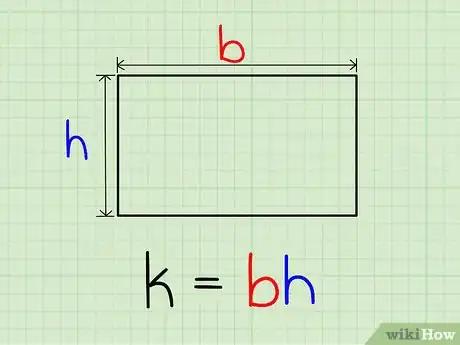
2Multiplica la base por la altura para obtener el área. Si el área del rectángulo es k, entonces k=b*h. Esto significa que el área es simplemente el producto de la base por la altura.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo hallar el área de un cuadrilátero.
Anuncio
Método 2
Método 2 de 10:Cuadrados
-
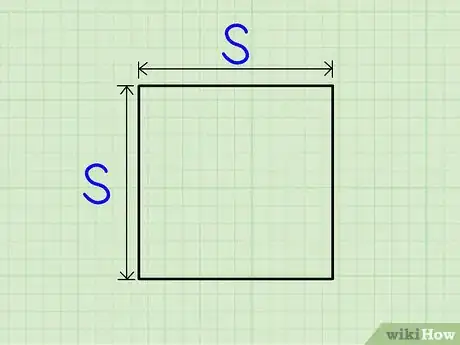
1Halla la longitud de un lado del cuadrado. Dado que los cuadrados tienen cuatro lados iguales, esta medida será válida para cualquiera de ellos.[2]
-
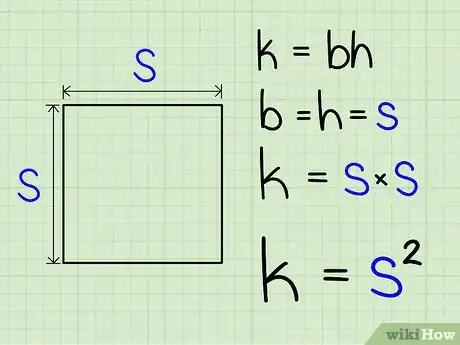
2Eleva la longitud del lado al cuadrado. Ya tienes el área.
- Este método funciona porque un cuadrado no es más que un rectángulo especial cuya longitud es igual a su ancho. Por lo tanto, al resolver la fórmula k=b*h, b y h tienen el mismo valor. Al final, solo tienes que elevar al cuadrado el valor numérico de una medida para hallar el área.
Anuncio
Método 3
Método 3 de 10:Paralelogramos
-
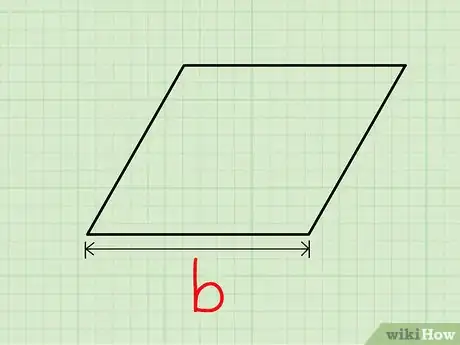
1Elige un lado como base del paralelogramo. Halla la medida de esta base.
-
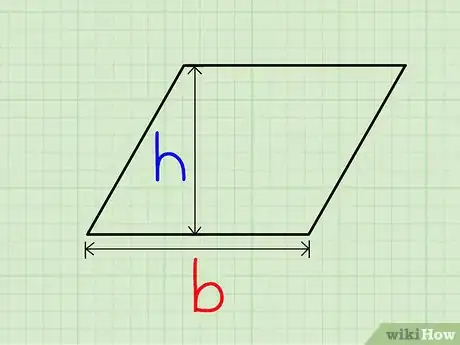
2Dibuja una línea perpendicular a esta base y determina su longitud desde el punto en el que corta a la base hasta el punto en que corta al lado opuesto a la base. Esta longitud es la altura.[3]
- Si el lado opuesto a la base no es suficientemente largo como para que la perpendicular lo corte, prolóngalo hasta que se interseque con la línea perpendicular.
-
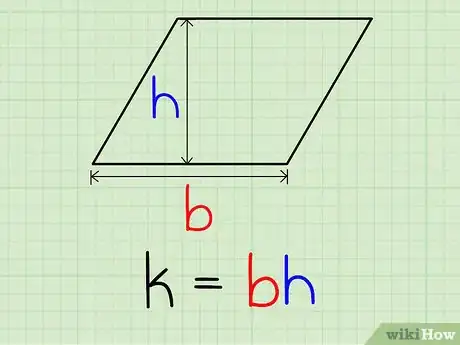
3Introduce la base y la altura en la ecuación k=b*h.[4]
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo calcular el área de un paralelogramo.
Anuncio
Método 4
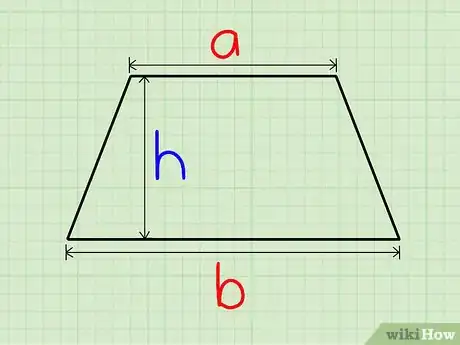
Método 4 de 10:Trapezoides
-
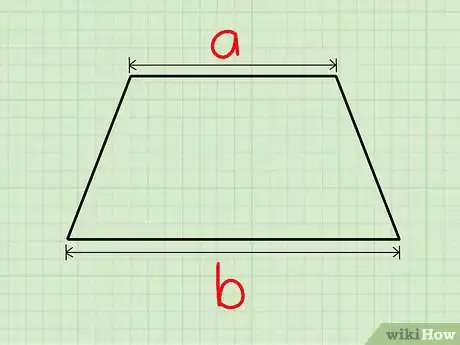
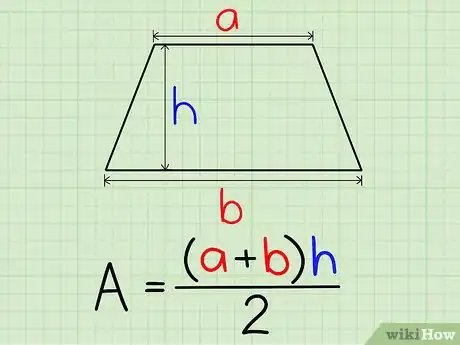
1Halla las longitudes de dos lados paralelos. Asigna estos valores a las variables a y b.
-
2Halla la altura. Dibuja una línea perpendicular que se interseque con ambos lados perpendiculares, de forma que la longitud del segmento obtenido entre esos dos puntos determine la altura del paralelogramo (h).[5]
-
3Introduce estos valores en la fórmula A=0,5(a+b)h.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo calcular el área de un trapezoide.
Anuncio
Método 5
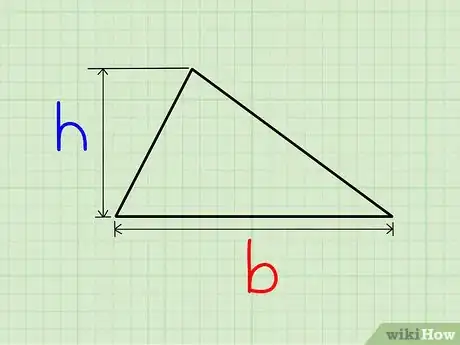
Método 5 de 10:Triángulos
-
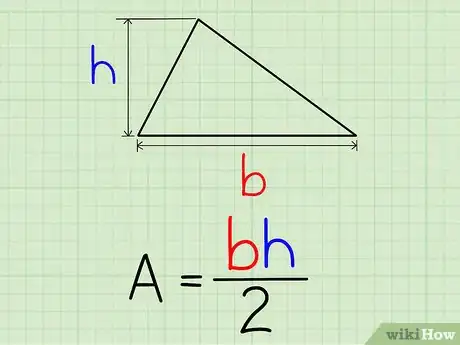
1Halla la base y la altura del triángulo. La base es la longitud de un lado del triángulo, y la altura es la longitud del segmento perpendicular que va desde la base hasta el vértice opuesto del triángulo.
-
2Para calcular el área, introduce los valores de la base y la altura en la ecuación A=0,5b*h.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo calcular el área de un triángulo.
Anuncio
Método 6
Método 6 de 10:Polígonos regulares
-
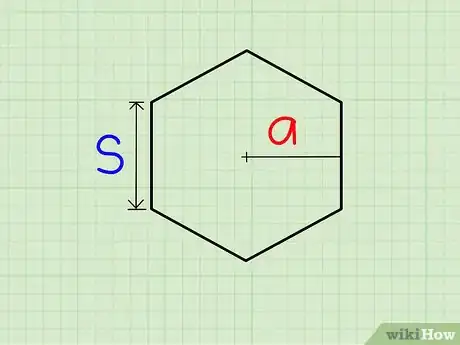
1Halla la longitud de un lado y la longitud de la apotema (el segmento perpendicular a un lado que conecta el punto medio de dicho lado con el centro del polígono). La longitud de la apotema se representará con la variable a.
-
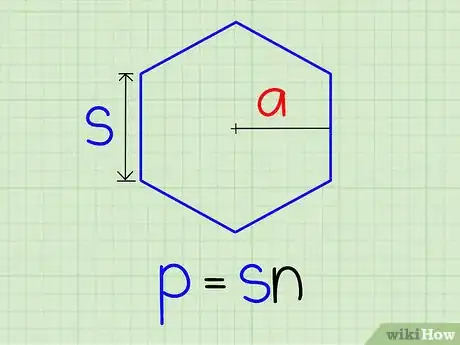
2Multiplica la longitud del lado por el número total de lados para obtener el perímetro del polígono (p).
-
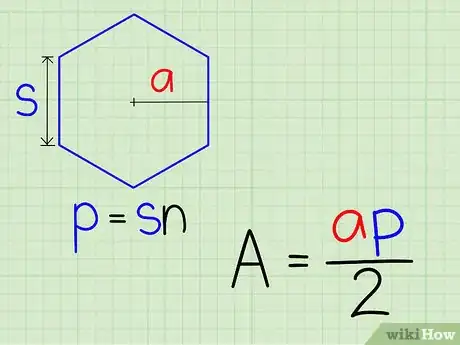
3Introduce estos valores en la ecuación A=0,5a*p.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo hallar el área de un polígono regular.
Anuncio
Método 7
Método 7 de 10:Círculos
-
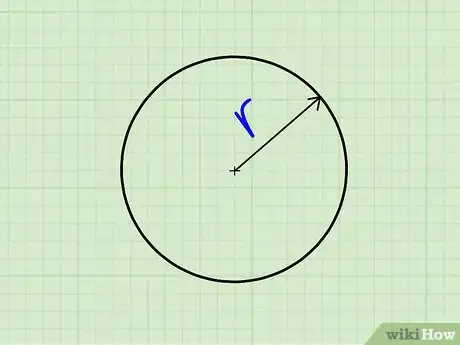
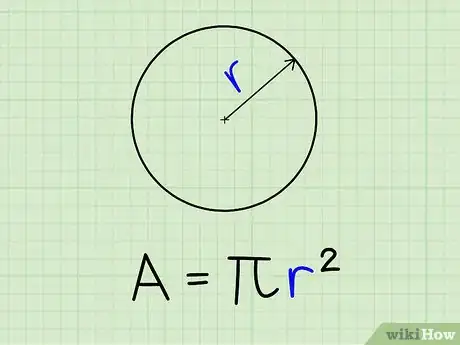
1Halla el radio del círculo (r). El radio es el segmento que conecta el centro del círculo con cualquier punto de la circunferencia que lo delimita. Por definición, este valor es siempre el mismo en cada círculo, independientemente del punto que elijas de la circunferencia.
-
2Introduce el valor del radio en la ecuación A=πr^2.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo calcular el área de un círculo.
Anuncio
Método 8
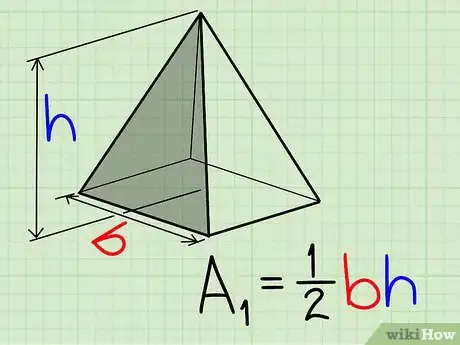
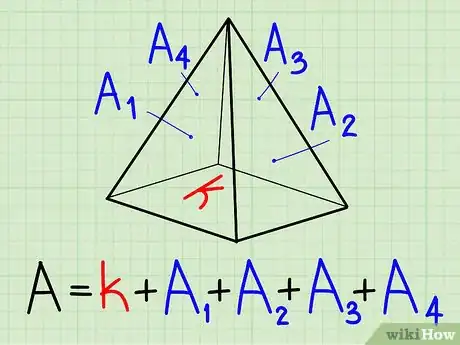
Método 8 de 10:Área de la superficie de una pirámide
-
1Halla el área de la base rectangular utilizando la fórmula anteriormente explicada en este artículo para calcular el área de un rectángulo: k=b*h.
-
2Halla el área de cada lado triangular utilizando la fórmula anteriormente explicada en este artículo para calcular el área de un triángulo: A=0,5b*h.
-
3Suma todas las áreas: la de la base y la de cada una de los lados.Anuncio
Método 9
Método 9 de 10:El área de la superficie de un cilindro
-
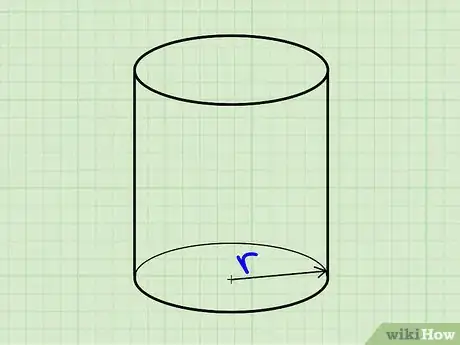
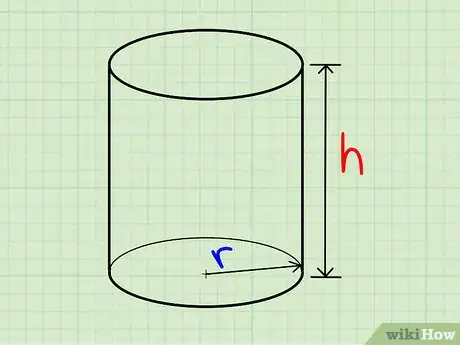
1Halla el radio de una de las dos bases circulares.
-
2Halla la altura del cilindro.
-
3Halla el área de las bases utilizando la fórmula del área de un círculo: A=πr^2.
-
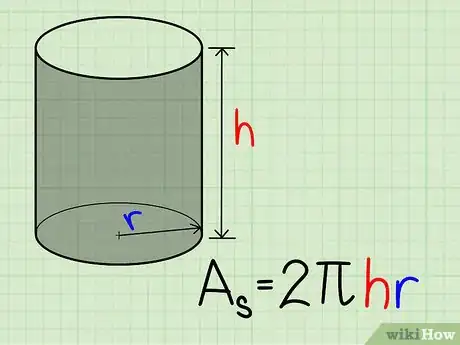
4Halla el área de la superficie lateral multiplicando la altura del cilindro por el perímetro de la base. El perímetro de una circunferencia es P=2πr, por lo que el área de la superficie lateral será: A=2πhr.
-
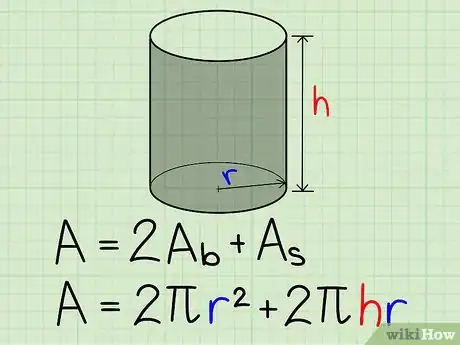
5Suma todas las áreas: las de las dos bases circulares e iguales entre sí, y la de la superficie lateral. Finalmente, obtenemos que el área de la superficie del cilindro es SA=2πr^2+2πhr.
- Si necesitas instrucciones más detalladas, consulta el artículo Cómo hallar el área de la superficie de un cilindro.
Anuncio
Método 10
Método 10 de 10:El área de una función
Supongamos que quieres hallar el área que se encuentra bajo una curva y por encima del eje x, definida por la función f(x) en el intervalo [a,b] de x. Este método requiere cierto conocimiento de cálculo integral. Si aún no has hecho ningún curso de introducción al cálculo, probablemente este método no tenga sentido para ti.
-
1Define f(x) en términos de x.
-
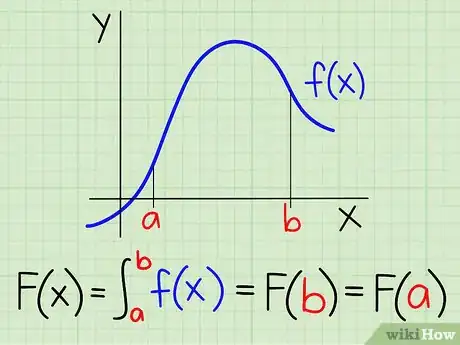
2Escribe la integral de f(x) en el intervalo [a,b]. Según el teorema fundamental del cálculo, dada una función F(x)=∫f(x), ∫abf(x) = F(b)—F(a).
-
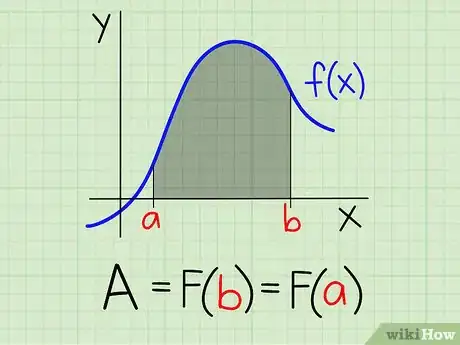
3Introduce los valores de a y b en la fórmula integral. El área que se encuentra por debajo de f(x) y en el intervalo [a,b] del eje x, se define como ∫abf(x). Por lo tanto, A=F(b))—F(a).Anuncio
Referencias
Acerca de este wikiHow
Para encontrar el área de un cuadrado, mide la longitud de cualquiera de sus lados y multiplícala por sí misma. Si la figura es un rectángulo, empieza por encontrar el área de un lado vertical y uno horizontal. Luego etiqueta el lado horizontal como la base y el vertical como la altura. Por último, multiplica la base por la altura. El resultado será el área.