Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 18 referencias citadas, que se pueden ver en la parte inferior de la página.
La geometría euclidiana tiene relación con las formas, las líneas y los ángulos y la manera como interactúan unos con otros. Se debe trabajar mucho al principio para aprender el lenguaje de la geometría. Después de aprender los postulados básicos y las propiedades de todas las formas y líneas, puedes comenzar a usar esta información para resolver problemas de geometría. Por desgracia, la geometría toma tiempo pero, si te esfuerzas, puedes comprenderla.
Pasos
Parte 1
Parte 1 de 3:Aprender los 5 postulados de Euclides
-
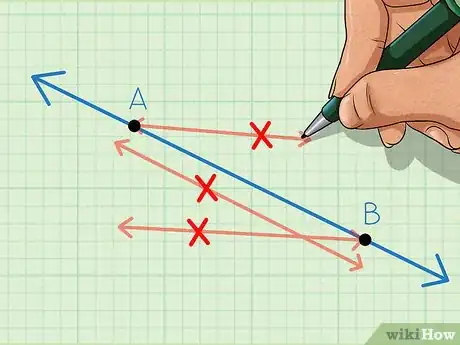
1Aprende el primer postulado. Un segmento de línea puede formarse uniendo dos puntos cualesquiera. Si tienes dos puntos A y B, puedes trazar un segmento de línea que los una. Solo puede hacerse un segmento de línea uniendo los dos puntos.[1]
-
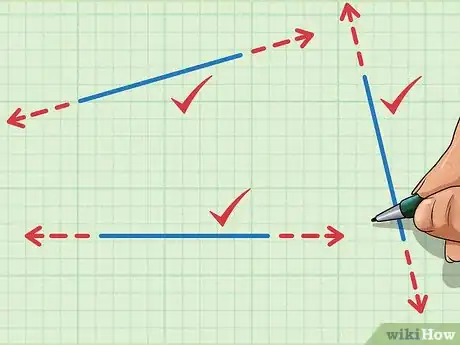
2Conoce el segundo postulado. Cualquier segmento de línea puede extenderse hacia el infinito en cualquier dirección. Después de construir un segmento de línea entre dos puntos, puedes extenderlo para formar una línea. Para ello, puedes extender cualquier extremo del segmento de manera infinita en la misma dirección.[2]
-
3Comprende el tercer postulado. Dada cualquier longitud y cualquier punto, puede trazarse un círculo con un punto como centro y la longitud como radio. Dicho de otro modo, puede dibujarse un círculo a partir de cualquier segmento de línea. Este postulado aplica independientemente de la longitud del segmento.[3]
-
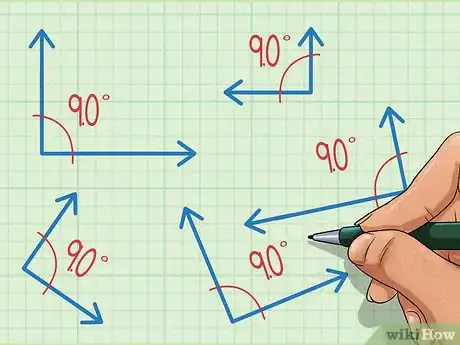
4Identifica el cuarto postulado. Todos los ángulos rectos son idénticos. Un ángulo recto equivale a 90 grados. Todos los ángulos rectos son congruentes o iguales. Si un ángulo no equivale a 90 grados, no es un ángulo recto.[4]
-
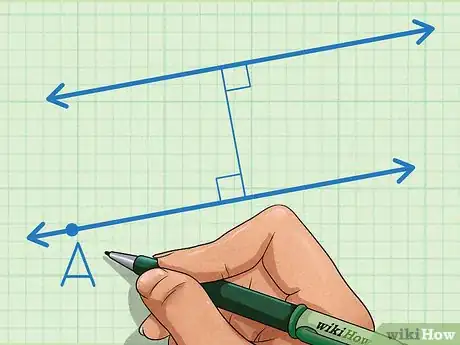
5Define el quinto postulado. Dada una línea y un punto, solo puede trazarse una línea a través del punto que esté en paralelo a la primera línea. Otra forma de expresar este postulado es decir que, si dos líneas cruzan una tercera de forma que la suma de sus ángulos interiores por un lado equivale a menos de dos ángulos rectos, ambas líneas a la larga se cruzarán. Estas dos líneas no están en paralelo una a la otra.[5]
- Este último postulado no puede comprobarse como un teorema. En la geometría no euclidiana, este postulado "paralelo" no aplica.
Parte 2
Parte 2 de 3:Comprender las formas, las líneas y los ángulos
-
1Conoce las propiedades de las líneas. Una línea se extiende de manera infinita en cualquier dirección y se denota mediante flechas en los extremos para indicarlo. Un segmento de línea es finito y existe únicamente entre dos puntos. Una semirrecta es un híbrido entre una línea y un segmento de línea: se extiende de manera infinita en una dirección desde un punto definido.[6]
- Una sola línea siempre medirá 180 grados.
- Dos líneas son paralelas si tienen la misma pendiente y nunca se cruzan.
- Las líneas perpendiculares son dos líneas que se unen para formar un ángulo de 90 grados.
- Las líneas intersecantes son dos líneas cualesquiera que se cruzan en un punto. Las líneas paralelas nunca pueden cruzarse, mientras que las perpendiculares sí.
-
2Aprende sobre los distintos tipos de ángulos. Existen tres tipos de ángulos: agudo, obtuso y recto. Un ángulo agudo es cualquier ángulo que mida menos de 90 grados. Un ángulo obtuso es un ángulo amplio y se define como cualquier ángulo que mida más de 90 grados. Un ángulo recto mide 90 grados exactamente.[7]
- Poder identificar los diversos tipos de ángulos es una parte fundamental de comprender la geometría.
- Dos líneas que formen un ángulo recto también son perpendiculares una a la otra. Forman una esquina perfecta.
- Asimismo, es posible que también observes una línea recta. Este ángulo mide 180 grados.
- Por ejemplo, un cuadrado o rectángulo tiene cuatro ángulos de 90 grados, en tanto que un círculo no tiene ninguno.
-
3Identifica los tipos de triángulos. Puedes identificar un triángulo de dos formas: por el tamaño de sus ángulos (agudo, obtuso y rectángulo) o por la cantidad de lados y ángulos que sean iguales (equilátero, isósceles y escaleno). En un triángulo agudo, todos los ángulos miden menos de 90 grados. Los triángulos obtusos tienen un ángulo que mida más de 90 grados, y un triángulo rectángulo tiene un ángulo de 90 grados.[8]
- Los triángulos equiláteros tienen tres lados iguales y tres ángulos que miden exactamente 60 grados.
- Los triángulos isósceles tienen dos lados iguales y dos ángulos iguales.
- Los triángulos escalenos no tienen lados ni ángulos iguales.
-
4Conoce la forma de determinar el perímetro y el área de las formas bidimensionales. Los cuadrados, rectángulos, círculos, triángulos, etc., son formas cuyos perímetros y áreas deberás saber calcular. El perímetro de un objeto es la medida de todos sus lados, en tanto que el área es la medida de la cantidad de espacio que ocupa.[9] [10] Estas son las ecuaciones para el perímetro y el área de las formas más comunes:[11]
- El perímetro de un círculo se conoce como la circunferencia y equivale a 2πr, en donde "r" es el radio.
- El área de un círculo es πr2, en donde "r" es el radio.
- El perímetro de un rectángulo es 2l + 2w, en donde "l" es la longitud y "w" es el ancho (por su abreviatura en inglés).
- El área de un rectángulo es l x w, en donde "l" es la longitud y "w" es el ancho (por su abreviatura en inglés).
- El perímetro de un triángulo es a + b + c, en donde cada variable denota un lado del triángulo.
- El área de un triángulo es ½bh, en donde "b" es la base del triángulo y "h" es la altura vertical (por su abreviatura en inglés).
-
5Calcula el área superficial y el volumen de los objetos tridimensionales. Al igual que es posible calcular el perímetro y el área de un objeto bidimensional, es posible encontrar el área superficial total y el volumen de un objeto tridimensional. Los objetos como las esferas, los prismas rectangulares, las pirámides y los cilindros tienen ecuaciones especiales para ello. El área superficial es el área total de toda la superficie del objeto, en tanto que el volumen constituye la cantidad total de espacio que ocupa.[12] [13]
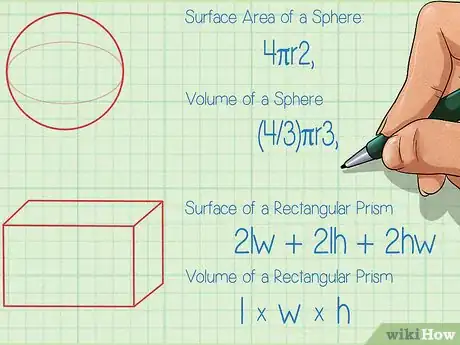
- El área superficial de una esfera equivale a 4πr2, en donde "r" es el radio de la esfera.
- El volumen de una esfera equivale a (4/3)πr3, en donde "r" es el radio de la esfera.
- El área superficial de un prisma rectangular es 2lw + 2lh + 2hw, en donde "l" es la longitud, "w" es el ancho y "h" es la altura (por sus abreviaturas en inglés).
- El volumen de un prisma rectangular es l x w x h, en donde "l" es la longitud, "w" es el ancho y "h" es la altura (por sus abreviaturas en inglés).
-
6Identifica pares de ángulos. Cuando una línea cruza otras dos líneas, se le conoce como una transversal. Estas líneas forman pares de ángulos. Los ángulos correspondientes son los dos ángulos en esquinas correspondientes contra la transversal.[14] Los ángulos alternos internos son los dos ángulos que se encuentran dentro de las dos líneas pero en lados opuestos de la transversal.[15] Los ángulos alternos externos son los dos ángulos que se encuentran fuera de las dos líneas pero en lados opuestos de la transversal.[16]
- Los pares de ángulos son equivalentes si dos de las líneas son paralelas.[17]
- Hay un cuarto par de ángulos: los ángulos interiores consecutivos. Estos son los dos ángulos que se encuentran dentro de las líneas y del mismo lado que la transversal. Cuando las dos líneas son paralelas, los ángulos interiores consecutivos siempre suman 180 grados.[18]
-
7Define el teorema de Pitágoras. El teorema de Pitágoras es una forma útil de determinar las longitudes de los lados de un triángulo rectángulo. Se define como a2 + b2 = c2, en donde "a" y "b" son la longitud y la altura (las líneas rectas) del triángulo y "c" es la hipotenusa (la línea en un ángulo). Si conoces dos lados de un triángulo, puedes calcular el tercero usando esta ecuación.[19]
- Por ejemplo, si tienes un triángulo rectángulo con los lados a = 3 y b = 4, puedes encontrar la hipotenusa:
- a2 + b2 = c2
- 32 + 42 = c2
- 9 + 16 = c2
- 25 = c2
- c = √25
- c = 25. La hipotenusa del triángulo es 5.
Parte 3
Parte 3 de 3:Resolver problemas de geometría
-
1Traza las figuras. Lee el problema y haz un diagrama para ilustrarlo. Etiqueta toda la información que se te dé, incluyendo todos los ángulos, las líneas paralelas o perpendiculares, y las líneas intersecantes. Una vez que tengas un bosquejo básico del problema, quizás debas dibujarlo todo otra vez. El segundo dibujo puede arreglar la escala de todo y asegurar que todos los ángulos se hayan trazado de una forma aproximadamente correcta.[20]
- Etiqueta también todas las incógnitas.
- La forma más fácil de comprender el problema es con un diagrama que esté dibujado con claridad.
-
2Haz observaciones según la información dada. Si se te da un segmento de línea pero hay ángulos que salen de él, sabrás que las medidas de todos los ángulos deben sumar 180 grados. Anota esta información en el diagrama o en los márgenes. Esta constituye una buena forma de pensar en lo que se te pregunta.
- Por ejemplo, los ángulos ABC y DBE forman una línea, ABE. El ángulo ABC = 120 grados. ¿Cuánto mide el ángulo DBE?
- La suma de los ángulos ABC y DBE debe ser 180, por lo que el ángulo DBE = 180 - el ángulo ABC.
- Ángulo DBE = 180 - 120 = 60 grados.
-
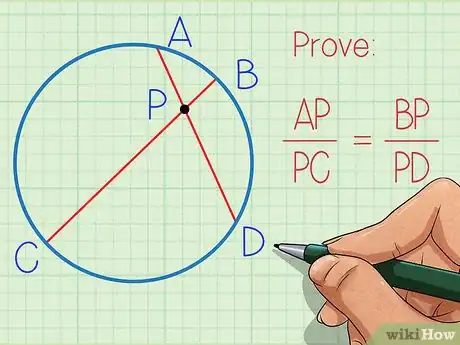
3Aplica teoremas básicos para responder a las preguntas. Muchos teoremas individuales que describen las propiedades de los triángulos, las líneas intersecantes y paralelas, y los círculos pueden usarse para resolver un problema. Identifica las formas geométricas del problema y busca los teoremas que apliquen. Utiliza pruebas y problemas antiguos como guía para fijarte si hay similitudes entre ellos. Estos son algunos de los teoremas geométricos generales que necesitarás:[21]
- La propiedad reflexiva: una variable equivale a sí misma. x = x.
- El postulado de la suma: cuando variables iguales se suman a variables iguales, todas las sumas son equivalentes. A + B + C = A + C + B.
- El postulado de la resta: este es similar al de la suma. Todas las variables que se restan a variables iguales tienen la misma diferencia. A – B – C = A – C – B.
- El postulado de sustitución: si dos cantidades son equivalentes, puedes sustituir una por la otra en cualquier expresión.
- El postulado de partición: cualquier todo equivale a la suma de todas sus partes. Línea ABC = AB + BC.
-
4Aprende los teoremas que aplican para los triángulos. Muchos problemas de geometría involucrarán triángulos, y te será de ayuda conocer sus propiedades para resolverlos. Usa estos teoremas para formular pruebas geométricas. Estos son algunos de los más importantes para los triángulos:[22]
- Las partes correspondientes de los triángulos congruentes son congruentes.
- LLL: lado-lado-lado. Si tres lados de un triángulo son congruentes con tres lados de un segundo triángulo, ambos son congruentes.
- LAL: lado-ángulo-lado. Si dos triángulos tienen un lado-ángulo-lado congruente, ambos son congruentes.
- ALA: ángulo-lado-ángulo. Si dos triángulos tienen un ángulo-lado-ángulo congruente, ambos son congruentes.
- AAA: ángulo-ángulo-ángulo. Los triángulos que tienen ángulos congruentes son similares pero no necesariamente congruentes.
Referencias
- ↑ http://mathworld.wolfram.com/EuclidsPostulates.html
- ↑ http://mathworld.wolfram.com/EuclidsPostulates.html
- ↑ http://mathworld.wolfram.com/EuclidsPostulates.html
- ↑ http://mathworld.wolfram.com/EuclidsPostulates.html
- ↑ http://mathworld.wolfram.com/EuclidsPostulates.html
- ↑ https://www.mathsisfun.com/geometry/line.html
- ↑ http://www.mathsisfun.com/angles.html
- ↑ http://www.mathsisfun.com/triangle.html
- ↑ https://www.mathsisfun.com/geometry/perimeter.html
- ↑ https://www.mathsisfun.com/geometry/area.html
- ↑ http://www.mathsisfun.com/area.html
- ↑ https://www.mathsisfun.com/definitions/surface-area.html
- ↑ https://www.mathsisfun.com/definitions/volume.html
- ↑ http://www.mathsisfun.com/geometry/corresponding-angles.html
- ↑ http://www.mathsisfun.com/geometry/alternate-interior-angles.html
- ↑ http://www.mathsisfun.com/geometry/alternate-exterior-angles.html
- ↑ http://www.mathsisfun.com/geometry/parallel-lines.html
- ↑ http://www.mathsisfun.com/geometry/consecutive-interior-angles.html
- ↑ http://www.mathsisfun.com/pythagoras.html
- ↑ http://www.homeschoolmath.net/teaching/geometry-2.php
- ↑ http://www.regentsprep.org/regents/math/geometry/gpb/theorems.htm
- ↑ http://www.mathwarehouse.com/geometry/congruent_triangles/

































wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.