Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 3401 veces.
Los triángulos congruentes son un par de triángulos idénticos que tienen 3 lados y 3 ángulos iguales.[1] Demostrar que dos triángulos son congruentes es una habilidad muy importante en la geometría. Dado que la respuesta depende del problema específico y de los datos que se te proporcionan, rara vez se usa el mismo proceso para hallarla. Esto puede ser frustante, pero existe un patrón general que puedes usar para demostrar la congruencia con pruebas basadas en la geometría. Puedes usar estas pautas específicas para comprobarlo. Una vez que las conozcas, podrás resolver los problemas que encuentres fácilmente.
Pasos
Parte 1
Parte 1 de 2:Demuestra la congruencia de los triángulos
-
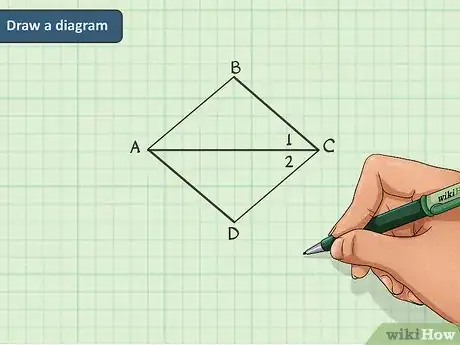
1Dibuja un diagrama. Es posible que se incluya uno en el planteamiento del problema, pero en el caso de que no sea así, es esencial que tú lo crees. Trata de dibujar con la mayor precisión posible. Utiliza toda la información que se te proporciona. Si hay dos lados o ángulos congruentes (iguales), márcalos como tales.[2]
- Podría ser buena idea crear un diagrama inicial que no sea tan exacto y luego volver a dibujarlo mejor una segunda vez.
- Si el diagrama tiene dos triángulos que se sobreponen, trata de dibujarlos separados. De esta manera será más sencillo hallar y marcar las partes congruentes.
- Si el diagrama no tiene dos triángulos, tal vez tengas que hallar otra cosa. Verifica el planteamiento del problema nuevamente para asegurarte de que se te pide demostrar la congruencia de dos triángulos.
-
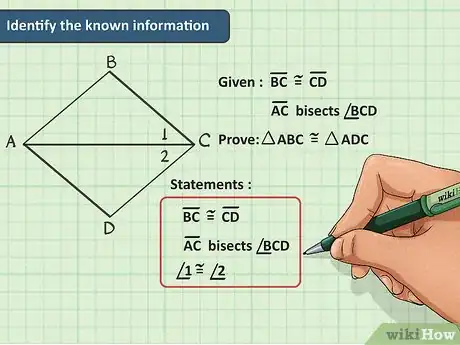
2Identifica la información conocida. Con los datos que tienes y tus conocimientos de geometría, puedes empezar a comprobar algunas cosas y a determinar si hay lados o ángulos congruentes en los dos triángulos. Examina tus hallazgos de manera lógica y determina la mejor manera apoyar tu conclusión en los datos proporcionados.[3]
- Por ejemplo, utiliza los siguientes datos para demostrar que los triángulos ABC y CDE son congruentes. C es el punto medio de la línea AE, BE es congruente con DA. Por definición, si C es el punto medio de AE, entonces AC debe ser congruente con CE. Esto te permite demostrar que por lo menos uno de los lados de cada uno de los triángulos son congruentes.
- Si BE es congruente con DA, entonces BC es congruente con CD, porque C también es el punto medio de la línea AD. Ahora sabes que tienes dos lados congruentes.
- Asimismo, dado que BE es congruente con DA, el ángulo BCA es congruente con el ángulo DCE, ya que los ángulos verticales son congruentes.
-
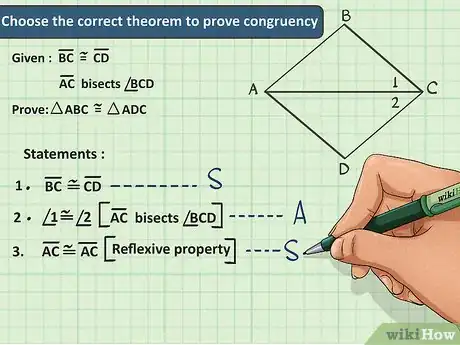
3Elige el teorema correcto para demostrar la congruencia de los triángulos. Existen cinco teoremas que puedes emplear este propósito. Una vez que identifiques toda la información que puedes a partir del planteamiento del problema, puedes decidir cuál de los teoremas te permitirá demostrar que los triángulos son congruentes.[4]
- Lado, lado, lado (LLL): ambos triángulos tienen tres lados iguales entre sí.
- Lado, ángulo, lado (LAL): dos de los lados de cada triángulo y el ángulo que los une (el ángulo entre los dos lados) son iguales.
- Ángulo, lado, ángulo (ALA): dos de los ángulos de cada triángulo y el lado que los une son iguales.
- Ángulo, ángulo, lado (AAL): dos ángulos y uno de los lados que no los une son iguales.
- Hipotenusa, cateto (HC): la hipotenusa y uno de los catetos de los dos triángulos son iguales. Este teorema solo se aplica para triángulos rectángulos.
- Siguiendo con el ejemplo, dado que pudiste demostrar que dos de los lados y el ángulo que los une son congruentes, tendrás que emplear el teorema lado, ángulo lado (LAL) para demostrar la congruencia de los triángulos.
Parte 2
Parte 2 de 2:Anotar la demostración
-
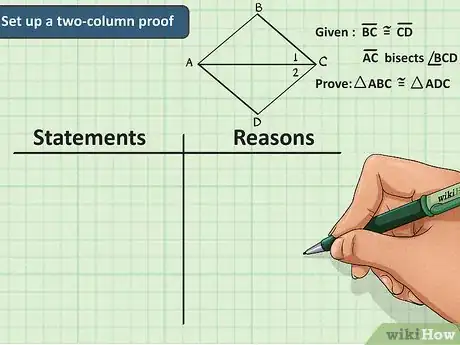
1Crea un espacio de dos columnas para fundamentar tu respuesta. La manera más común de hacer la demostración es con dos columnas. En uno de los lados, escribe las declaraciones, y en la otra, las razones o demostración. Toda declaración debe ir acompañada de una razón que demuestre su veracidad. Entre estas razones, puedes incluir los datos que se proporcionan en el planteamiento del problema, así como definiciones, postulados y teoremas de geometría.[5]
-
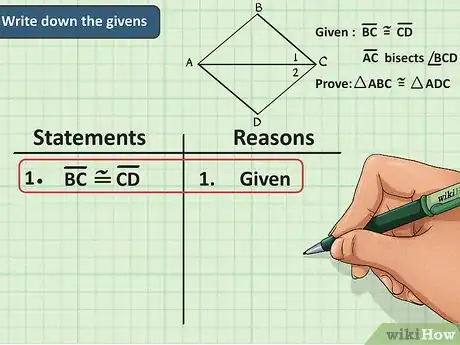
2Escribe los datos del problema. El paso más sencillo es anotar los datos que ya tienes. En un lado, coloca tu declaración y en la columna de la demostración, simplemente pon la información relevante. Puedes anotar todos los datos al inicio o colocarlos siguiendo un orden que tenga sentido con el resto de tu demostración.[6]
- Escribe lo que quieres demostrar. Si la idea es probar que los triángulos ABC y XYZ son congruentes, esto debe ir en la parte superior de la columna de las pruebas. Esto también servirá como conclusión.
-
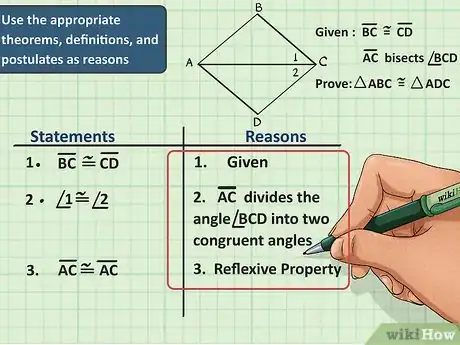
3Utiliza los teoremas, definiciones y postulados correctos como parte de la demostración. Necesitarás tener una base sólida en geometría antes de poder comenzar a escribir las razones. Conocer los teoremas, definiciones y postulados relevantes es lo más importante. Saber esta parte teórica de la geometría te ayudará a hallar las razones que necesitas para fundamentar tu respuesta.[7]
- Algunas definiciones y postulados que debes conocer son las líneas, ángulos, puntos medios de una línea, bisectrices, ángulos alternos y ángulos interiores, etc.
- No puedes comprobar un teorema en sí. Si quieres demostrar que los ángulos base son congruentes, no puedes escribir “los ángulos base son congruentes” como razón para tu respuesta.
-
4Ordena las razones de tu respuesta de manera lógica. Cuando quieres demostrar algo, debes pensar de manera lógica. Trata de ordenar todos los pasos que seguiste para crear una secuencia natural. A veces es buena idea resolver el problema de atrás para adelante: empieza por la conclusión y luego continúa hasta llegar al primer paso.[8]
- Es necesario incluir todos los pasos seguidos, incluso si parecen muy obvios o poco importantes.
- Una vez que termines, lee la demostración para ver si tiene sentido.
Consejos
- Si los datos del problema incluyen la palabra “perpendicular”, no digas que el ángulo es de 90 grados solo por la definición de las líneas perpendiculares. Es mejor escribir una oración que diga que dicho ángulo es un ángulo recto por “la definición de las líneas perpendiculares” y luego añadir otra oración que diga que el ángulo mide 90 grados debido a la “definición de un ángulo recto”.
Referencias
- ↑ http://www.mathsisfun.com/geometry/triangles-congruent-finding.html
- ↑ https://www.wyzant.com/resources/lessons/math/geometry/introduction/two_column_proofs
- ↑ http://www.ck12.org/geometry/Two-Column-Proofs/lesson/Two-Column-Proofs-BSC-GEOM/
- ↑ http://www.mathsisfun.com/geometry/triangles-congruent-finding.html
- ↑ https://www.wyzant.com/resources/lessons/math/geometry/introduction/two_column_proofs
- ↑ https://www.wyzant.com/resources/lessons/math/geometry/introduction/two_column_proofs
- ↑ http://www.ck12.org/geometry/Two-Column-Proofs/lesson/Two-Column-Proofs-BSC-GEOM/
- ↑ https://www.wyzant.com/resources/lessons/math/geometry/introduction/two_column_proofs
























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 3401 veces.