Cómo demostrar la propiedad de la suma de los ángulos de un triángulo

Coescrito por Personal de wikiHow

Se sabe que la suma de todos los ángulos interiores de un triángulo equivale a 180º, pero ¿por qué? Para demostrar que la suma de todos los ángulos de un triángulo es igual a 180 grados, debes comprender algunos teoremas básicos de la geometría. Aplicando algunos de estos conceptos, podrás desarrollar por escrito una prueba muy simple.

Parte 1
Parte 1 de 2:
Demostrar la propiedad de la suma de los ángulos

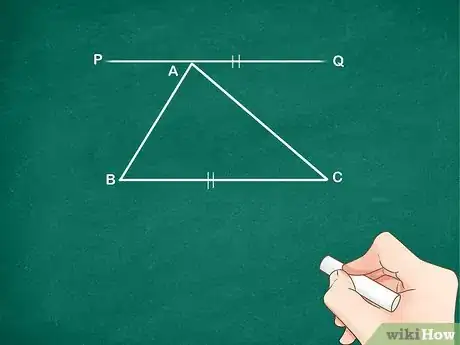
  1. Imagen titulada Prove the Angle Sum Property of a Triangle Step 1
    1
    Dibuja una línea paralela al lado BC del triángulo que pase por el vértice A. Etiqueta esa línea como PQ. Asegúrate de que esta línea sea paralela a la base de triángulo.[1]
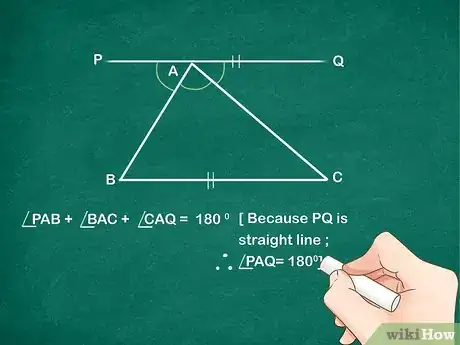
  2. Imagen titulada Prove the Angle Sum Property of a Triangle Step 2
    2
    Escribe la ecuación ángulo PAB + ángulo BAC + ángulo CAQ = 180 grados. Recuerda que todos los ángulos que comprenden una línea recta equivalen siempre a 180º. Como el ángulo PAB, el ángulo BAC y el ángulo CAQ se combinan entre sí para formar la línea PQ, sus ángulos deben sumar 180º. Esta será la Ecuación 1.[2]
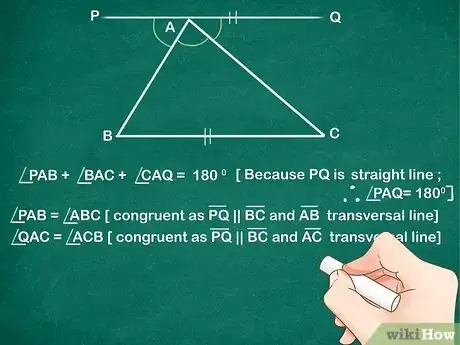
  3. Imagen titulada Prove the Angle Sum Property of a Triangle Step 3
    3
    Establece que el ángulo PAB = ángulo ABC y que ángulo CAQ = ángulo ACB. La línea PQ que has dibujado es paralela al lado BC del triángulo, por consiguiente, los ángulos alternos internos (PAB y ABC) que se forman a partir de la línea transversal AB son congruentes. Del mismo modo, los ángulos alternos internos (CAQ y ACB) que se forman a partir de la línea transversal AC también son congruentes.[3]
    • Ecuación 2: ángulo PAB = ángulo ABC
    • Ecuación 3: ángulo CAQ = ángulo ACB
    • Existe un teorema de la geometría que establece que los ángulos alternos internos de líneas paralelas son congruentes.[4]
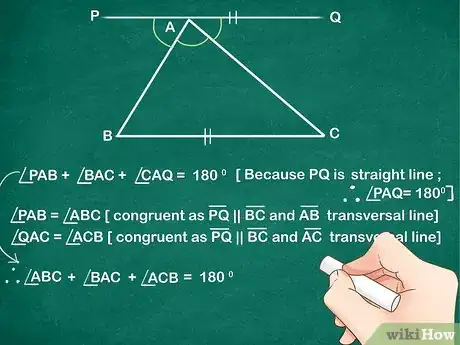
  4. Imagen titulada Prove the Angle Sum Property of a Triangle Step 4
    4
    Sustituye el ángulo PAB y el ángulo CAQ en la Ecuación 1 por el ángulo ABC y el ángulo ACB (basándote en lo que establece la Ecuación 2 y la Ecuación 3) respectivamente. Sabiendo que los ángulos alternos internos son iguales, ahora sustituye los ángulos del triángulo por los de la línea.[5]
    • Ahora la ecuación quedará así: ángulo ABC + ángulo BAC + ángulo ACB = 180º.
    • En otras palabras, en el triángulo ABC, el ángulo B + el ángulo A + el ángulo C = 180º. Por consiguiente, la suma de todos los ángulos de un triángulo es igual a 180º.
    Anuncio

Parte 2
Parte 2 de 2:
Comprender la propiedad de la suma de los ángulos

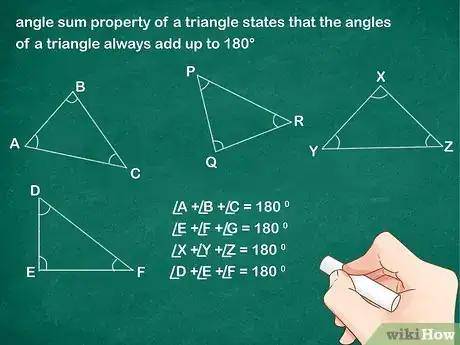
  1. Imagen titulada Prove the Angle Sum Property of a Triangle Step 5
    1
    Define la propiedad de la suma de los ángulos. La propiedad de la suma de los ángulos de un triángulo establece que los ángulos de cualquier triángulo siempre suman 180º.[6] Todos los triángulos tienen 3 ángulos y, ya sean agudos, obtusos o rectángulos, estos suman siempre 180º.
    • Por ejemplo, en el triángulo ABC, el ángulo A + el ángulo B + el ángulo C = 180º.
    • Este teorema es muy útil para hallar la medida de un ángulo desconocido cuando conoces los otros dos.
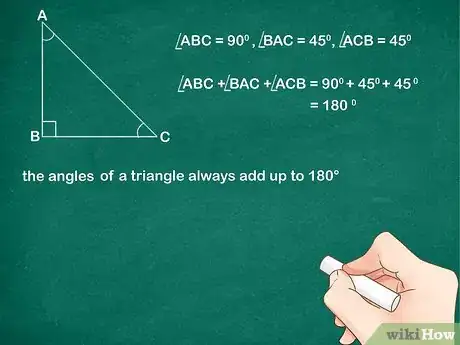
  2. Imagen titulada Prove the Angle Sum Property of a Triangle Step 6
    2
    Analiza algunos ejemplos. Para poder realmente incorporar este concepto, sería bueno que estudies algunos ejemplos. Piensa en el caso de los triángulos rectángulos donde uno de sus ángulos es de 90º y los otros dos miden 45º. Suma 90º + 45º + 45º y verás que es 180º. Analiza otros triángulos de distintas formas y tamaños y suma sus ángulos. Verás que siempre suman 180º.[7]
    • En el ejemplo del triángulo rectángulo: ángulo A = 90º, ángulo B = 45º y ángulo C = 45º. El teorema establece que ángulo A + ángulo B + ángulo C = 180º. La suma de estos ángulos da 90° + 45° + 45° = 180°. Por lo tanto, el lado izquierdo de la ecuación es igual al lado derecho.
  3. Imagen titulada Prove the Angle Sum Property of a Triangle Step 7
    3
    Utiliza este teorema para encontrar un ángulo desconocido. Basándote en el teorema de la suma de los ángulos y aplicando simples pasos algebraicos puedes encontrar un ángulo desconocido de un triángulo si conoces los otros dos. Reordena la ecuación básica para encontrar el ángulo desconocido.
    • Por ejemplo, en el triángulo ABC, el ángulo A = 67º y el ángulo B = 43º. El ángulo C es desconocido.
    • ángulo A + ángulo B + ángulo C = 180º
    • 67º + 43º + ángulo C = 180º
    • ángulo C = 180º - 67º - 43º
    • ángulo C = 70º
    Anuncio

wikiHows relacionados

calcular el radio de un círculo
Cómo
calcular el radio de un círculo
calcular la circunferencia de un círculo
Cómo
calcular la circunferencia de un círculo
encontrar el vértice de una ecuación cuadrática
Cómo
encontrar el vértice de una ecuación cuadrática
sacar el área de un cuadrilátero
Cómo
sacar el área de un cuadrilátero
calcular ángulos
Cómo
calcular ángulos
calcular la circunferencia
Cómo
calcular la circunferencia
encontrar el radio de una esfera
Cómo
encontrar el radio de una esfera
sacar el volumen de un cubo
Cómo
sacar el volumen de un cubo
calcular cuántas diagonales tiene un polígono
Cómo
calcular cuántas diagonales tiene un polígono
encontrar la magnitud de un vector
Cómo
encontrar la magnitud de un vector
medir un ángulo sin usar un transportador
Cómo
medir un ángulo sin usar un transportador
sacar el angulo de un triangulo
Cómo
sacar el angulo de un triangulo
calcular metros cuadrados
Cómo
calcular metros cuadrados
dibujar un hexágono
Cómo
dibujar un hexágono
Anuncio

Referencias

  1. ↑ http://hotmath.com/hotmath_help/topics/angle-sum-theorem.html
  2. ↑ http://www.basic-mathematics.com/angle-sum-theorem.html
  3. ↑ http://www.basic-mathematics.com/angle-sum-theorem.html
  4. ↑ http://www.basic-mathematics.com/angle-sum-theorem.html
  5. ↑ http://hotmath.com/hotmath_help/topics/angle-sum-theorem.html
  6. ↑ http://www.algebraden.com/angle-sum-property-of-triangle.htm
  7. ↑ http://www.algebraden.com/angle-sum-property-of-triangle.htm

Acerca de este wikiHow

Personal de wikiHow
Coescrito por:
Personal de wikiHow
wikiHow Staff Writer
Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.

wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 10 242 veces.
Categorías: Geometría
Anuncio