Cómo descomponer un vector en sus componentes

Coescrito por Personal de wikiHow

Un vector es una representación gráfica de una fuerza física. Puede representar un movimiento, como el de un avión que viaja hacia el noreste a 640 km/h (400 mph), o incluso una fuerza, como la de una pelota que gira por una mesa y cae en diagonal debido a la gravedad y su velocidad inicial. Por lo general, será de mucha utilidad poder calcular los componentes de un vector, es decir, la fuerza (o velocidad, o lo que sea que el vector mide) aplicada tanto en una dirección horizontal como en una vertical. Para ello, puedes utilizar gráficos y un poco de geometría simple. Si quieres hacer cálculos más exactos, deberás utilizas la trigonometría.

Método 1

Método 1 de 4:
Identificar los componentes por medio de gráficos

1
Elige una escala adecuada. Para graficar el vector y sus componentes, deberás determinar una escala donde colocar el gráfico. Elige una con el tamaño suficiente como para trabajar de manera cómoda y precisa, pero que sea lo suficientemente pequeña como para poder dibujar el vector a escala.^{[1]
X
Fuente de investigación}
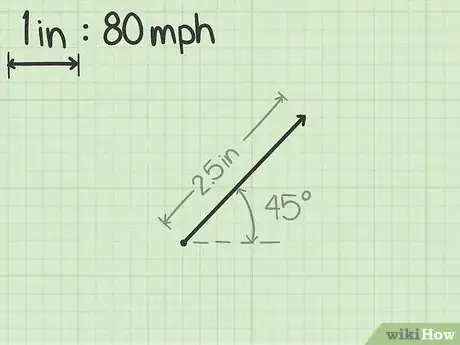
- Por ejemplo, supongamos que tienes un vector que representa una velocidad de 320 km/h (200 mph) que va en dirección noreste. Si utilizas un papel cuadriculado estándar de 4 cuadrículas por cada 2,5 cm (1 pulgada), entonces a cada cuadrado asígnale un valor de 32 km/h (20 mph). Esto representará una escala donde 2,5 cm (1 pulgada) equivalen a 128 km/h (80 mph).
- No necesitas dibujar un diagrama con un eje “x” y un eje “y”, pues la ubicación del vector con respecto al origen es irrelevante. Tu objetivo será el vector mismo y no su ubicación en el espacio bidimensional o tridimensional. El papel cuadriculado solo te servirá como una herramienta de medición, de modo que la ubicación no importa.
2
Dibuja el vector a escala. Es importante que dibujes el vector con la mayor precisión posible, pues en el gráfico deberás representar tanto su dirección como su longitud correctas.^{[2]
X
Fuente de investigación}
- Te será de utilidad emplear una regla precisa. Por ejemplo, si has elegido la escala de una cuadrícula que representa 32 km/h (20 mph) y cada una mide unos 0,5 cm (1/4 de pulgada), entonces un vector de 320 km/h (200 mph) será una línea de 10 cuadrículas (2 ½ pulgadas) de largo.
- Si es necesario, utiliza un transportador para mostrar el ángulo o la dirección del vector. Por ejemplo, si el vector muestra movimiento en dirección noreste, deberás dibujar una línea en un ángulo de 45 grados que parta desde la horizontal.
- La dirección del vector puede indicar muchas clases distintas de medidas de dirección. Si vas a representar un recorrido, podría tratarse de una dirección en el mapa. En el caso del recorrido de un objeto lanzado o golpeado, el ángulo del vector podría ser el ángulo de viaje desde el suelo. En física nuclear, un vector puede indicar la dirección de un electrón.
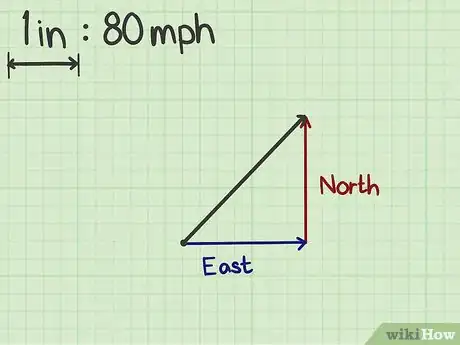
3
Dibuja un triángulo rectángulo donde el vector sea la hipotenusa. Con una regla, dibuja una línea horizontal desde la cola del vector que sea lo suficientemente amplia como para que coincida con la cabeza de este. Haz una punta de flecha en la punta de dicha línea para indicar que también es un vector componente. Luego, traza una línea vertical desde ese punto hacia la cabeza del vector original e igualmente haz una punta de flecha en este punto.^{[3]
X
Fuente de investigación}
- Ahora debes tener un triángulo rectángulo formado por tres vectores. El vector original será la hipotenusa, mientras que la base es un vector horizontal y la altura, un vector vertical.
- Existen dos excepciones en las que no puedes formar un triángulo rectángulo. Esto pasa en las ocasiones en que el vector original es exactamente horizontal o vertical. En el caso de que el vector sea horizontal o vertical, el componente siempre será cero.
4
Etiqueta los dos vectores componentes. Dependiendo de lo que represente el vector original, deberás etiquetar los dos vectores componentes que acabas de dibujar. Por ejemplo, si el vector original representa un recorrido en dirección noreste, el vector horizontal representará el “este”, mientras que el vertical, el “norte”.^{[4]
X
Fuente de investigación}
- Otros componentes podrían ser “arriba y abajo” o “izquierda y derecha”.
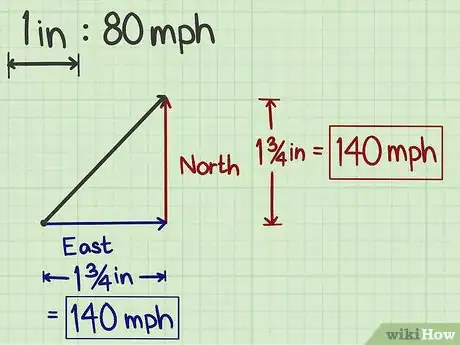
5
Mide los vectores componentes. Para determinar las magnitudes de dos vectores componentes, puedes únicamente el papel cuadriculado o una regla. Si usas esta última, mide la longitud de cada vector y haz la conversión utilizando la escala que elegiste. Por ejemplo, una línea horizontal que mide 3 cm (1 ¼ pulgada) de largo representaría un componente este de 160 km/h (100 mph) en una escala donde 2,5 cm (1 pulgada) = 128 km/h (80 mph).^{[5]
X
Fuente de investigación}
- Si utilizas el papel cuadriculado en lugar de la regla, probablemente necesites hacer algunas estimaciones. Si la línea cruza tres cuadrados completos y termina en el medio de un cuarto, necesitarás estimar la fracción de dicho cuadrado y multiplicarla por la escala que elegiste. Por ejemplo, si un cuadrado equivale a 32 km/h (20 mph) y estimas que un vector componente mide 3 ½ cuadrados, entonces dicho vector representa a 112 km/h (70 mph).
- También mide los vectores componentes horizontal y vertical, y luego etiqueta los resultados.

Método 2

Método 2 de 4:
Calcular los componentes utilizando cálculos trigonométricos

1
Haz una descripción esquemática del vector original. Si haces cálculos matemáticos, no es necesario que el gráfico sea completamente preciso ni tampoco hace falta que determines alguna escala de medida. Simplemente dibuja un rayo que siga la dirección general del vector que vas a calcular. Etiqueta el vector que hayas dibujado con su magnitud y el ángulo que forma en relación con la horizontal.^{[6]
X
Fuente de investigación}
- Por ejemplo, imagina un cohete que es lanzado en un ángulo de 60 grados a una velocidad de 1500 metros (5000 pies) por segundo. Deberás dibujar un rayo que apunte en diagonal hacia arriba, y etiquetar su longitud como “1500 m/s” y su ángulo como “60°”.
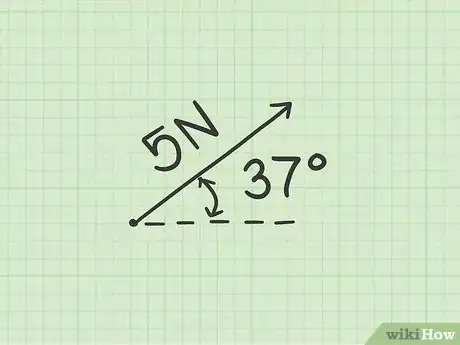
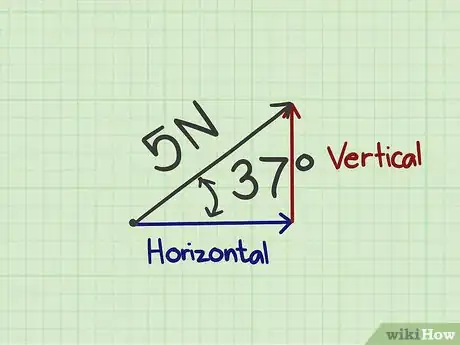
- El diagrama mostrado anteriormente indica un vector de fuerza de 5 newtons en un ángulo de 37 grados con relación a la horizontal.
2
Dibuja y etiqueta los vectores componentes. Dibuja un rayo horizontal que comience en la base del vector original y apunte en su misma dirección (izquierda o derecha). Esto representará el componente horizontal del vector original. Luego, dibuja un rayo vertical que conecte la punta del vector horizontal con la del original. Esto representará el componente vertical del vector original.^{[7]
X
Fuente de investigación}
- Los componentes horizontal y vertical de un vector representan una forma teórico-matemática de descomponer una fuerza en dos partes. Imagina un telesketch que tiene dos perillas de dibujo para las líneas “vertical” y “horizontal”. Si dibujaste una línea utilizando únicamente la perilla “vertical” y luego una con la perilla “horizontal”, llegarías al mismo punto que si hubieras girado ambas perillas exactamente a la misma velocidad. Esto ilustra el efecto simultáneo que una fuerza horizontal y vertical tiene sobre un objeto.
3
Utiliza la función seno para calcular el componente vertical. Debido a que los componentes de un vector crean un triángulo rectángulo, puedes hacer cálculos trigonométricos para obtener medidas exactas de dichos componentes. Utiliza la siguiente ecuación:^{[8]
X
Fuente de investigación}
- $\sin \theta ={\frac {\text{vertical}}{\text{hipotenusa}}}$
- Siguiendo con el ejemplo del misil, puedes calcular el componente vertical al reemplazar los valores que conoces y luego realizar una simplificación de la siguiente manera:
  - $\operatorname {sen} \theta ={\frac {\text{vertical}}{\text{hipotenusa}}}$
  - $\operatorname {sen}(60)={\frac {\text{vertical}}{1500}}$
  - $1500\operatorname {sen}(60)={\text{vertical}}$
  - $1500*0,866={\text{vertical}}$
  - $1299$
- Etiqueta el resultado con las unidades respectivas. En este caso, el componente vertical representa una velocidad ascendente de 1299 m (4000 pies) por segundo.
- El diagrama anterior muestra un ejemplo alternativo y calcula los componentes de una fuerza de 5 newtons en un ángulo de 37 grados. Utilizando la función seno, se calcula que la fuerza vertical es de 3 newtons.
4
Utiliza la función coseno para calcular el componente horizontal. De la misma manera en que utilizas el seno para calcular el componente vertical, puedes utilizar el coseno para hallar la magnitud del componente horizontal. Utiliza la siguiente ecuación:^{[9]
X
Fuente de investigación}
- $\cos \theta ={\frac {\text{horizontal}}{\text{hipotenusa}}}$
- Utiliza los detalles en el ejemplo del misil para hallar su componente horizontal de la siguiente manera:
  - $\cos \theta ={\frac {\text{horizontal}}{\text{hipotenusa}}}$
  - $\cos(60)={\frac {\text{horizontal}}{1500}}$
  - $1500\cos(60)={\text{horizontal}}$
  - $1500*0,5={\text{horizontal}}$
  - $750$
- Etiqueta el resultado con las unidades respectivas. En este caso, el componente horizontal representa una velocidad de avance (o hacia la izquierda, derecha o atrás) de 750 metros (2000 pies) por segundo.
- El diagrama anterior muestra un ejemplo alternativo, donde se calcula los componentes de una fuerza de 5 newtons en un ángulo de 37 grados. Utilizando la función coseno, se calcula que la fuerza horizontal es de 4 newtons.

Método 3

Método 3 de 4:
Utilizar componentes vectoriales para sumar más vectores

1
Entiende el significado de “sumar” vectores. Por lo general, la suma es un concepto muy sencillo, pero contiene un significado especial cuando se trata de vectores. Un solo vector representa un movimiento, una fuerza o algún otro elemento físico que ejerce una acción sobre un objeto. Si hay dos o más fuerzas actuando al mismo tiempo, podrás “sumarlas” para hallar la fuerza resultante ejercida sobre un objeto.
- Por ejemplo, piensa en una pelota de golf que se golpea en el aire. Una de las fuerzas que actúan sobre ella es la fuerza del golpe inicial, la cual se compone de un ángulo y una magnitud. Otra de las fuerzas podría ser el viento, el cual tiene su propio ángulo y magnitud. Al sumar ambas fuerzas, podrás describir el recorrido resultante de la pelota.
2
Descompón cada vector en sus partes componentes. Antes de sumar los vectores, deberás determinar los componentes de cada uno de ellos. Utiliza los procesos descritos en este artículo para hallar los componentes horizontales y verticales de cada fuerza.
- Por ejemplo, supongamos que la pelota de golf recibe un golpe en un ángulo ascendente de 30 grados y a una velocidad de 210 km/h (130 mph). Utiliza un cálculo trigonométrico para hallar los dos vectores componentes:
  - ${\text{Vertical}}=210\operatorname {sen}(30)=104,6{\text{km/h}}$
  - ${\text{Horizontal}}=210\cos(30)=181,2{\text{km/h}}$
- Ahora ten en cuenta el vector que representa la fuerza del viento. Supongamos que el viento sopla la pelota en un ángulo descendente de 10 grados a una velocidad de 16 km/h (10 mph) (ignoremos las fuerzas izquierda y derecha para simplificar los cálculos). Los dos componentes del viento pueden calcularse de manera similar:
  - ${\text{Vertical}}=16\operatorname {sen}(-10)=-2,8{\text{km/h}}$
  - ${\text{Horizontal}}=16\cos(-10)=15,85{\text{km/h}}$
  - Ten en cuenta que utilizamos un ángulo de -10 grados debido a que el viento sopla hacia abajo contraponiéndose a la fuerza del golpe.
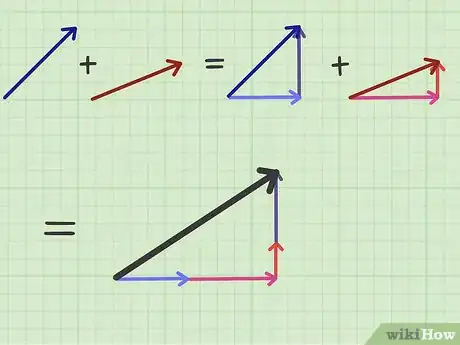
3
Suma los componentes. Debido a que los vectores componentes siempre se miden en ángulos rectos, puedes sumarlos directamente. Haz coincidir entre sí los componentes horizontales de un vector y haz lo mismo con los componentes verticales.
- En este ejemplo, el vector vertical resultante es la suma de los dos componentes:
  - ${\text{Vertical}}=104,6+(-2,8)=101,81$
  - ${\text{Horizontal}}=181,2+15,85=197,06$
- Interpreta el significado de estos resultados. La fuerza neta que actúa sobre la pelota de golf, debido tanto a la fuerza del golpe como del viento, equivale a una sola fuerza con componentes de 101,81 km/h (63,26 mph) en vertical y 197 km/h (122,45 mph) en horizontal.
4
Utiliza el Teorema de Pitágoras para hallar la magnitud del vector resultante. Por último, probablemente quieras saber el efecto neto que tienen el swing (movimiento oscilante que se hace al golpear la pelota) y el viento sobre la pelota. Si conoces ambos componentes, puedes reemplazarlos en el Teorema de Pitágoras para hallar la magnitud del vector resultante.
- Recuerda que los vectores componentes representan las patas de un triángulo rectángulo y que el vector resultante es su hipotenusa. Utilizando el Teorema de Pitágoras, $c^{2}=a^{2}+b^{2}$ $c^{2}=a^{2}+b^{2}$ , podrás realizar dicho cálculo de la siguiente manera:
  - ${\text{Resultante}}^{2}=101,81^{2}+197,06^{2}$
  - ${\text{Resultante}}^{2}=30570,82$
  - ${\text{Resultante}}={\sqrt {30570,82}}$
  - ${\text{Resultante}}=221,81$
- Por lo tanto, el vector resultante representa una sola fuerza ejercida sobre la pelota, con una magnitud de unos 221,81 km/h (137,83 mph). Ten en cuenta que dicha magnitud es ligeramente mayor que la fuerza del golpe inicial, pues el viento empuja la pelota hacia adelante y hacia abajo al mismo tiempo.
5
Utiliza un cálculo trigonométrico para hallar el ángulo del vector resultante. Saber la fuerza del vector resultante es la mitad de la solución. La otra mitad consiste en hallar el ángulo neto de dicho vector. En este ejemplo, debido a que el swing aplica una fuerza ascendente y el viento aplica una fuerza descendente aunque menor, necesitarás hallar el ángulo resultante.
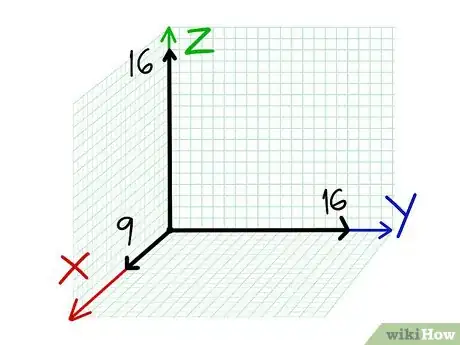
- Dibuja un triángulo rectángulo y etiqueta los componentes. La base horizontal representa el componente vectorial que va hacia adelante con una velocidad de 197,3 km/h (122,45 mph), mientras que la pata vertical representa el componente vectorial ascendente con una velocidad de 101,81 km/h (63,26 mph). Por último, la hipotenusa representa el vector resultante con una magnitud de 221,81 km/h (137,83 mph).
- Para hallar el ángulo, puedes elegir la función seno, con el componente vertical; o la función coseno, con el componente horizontal. El resultado será el mismo.
  - $\operatorname {sen} \theta ={\frac {101,81}{197,06}}$
  - $\operatorname {sen} \theta =0,459$
  - $\theta =\arcsin(0,459)$
  - $\theta =27,32$
- Por lo tanto, el vector resultante representa una única fuerza que actúa sobre la pelota en un ángulo ascendente de 27,32 grados. Esto tiene sentido, pues es ligeramente menor que el ángulo del swing de 30 grados debido a la fuerza descendente del viento. No obstante, en este ejemplo, el swing es una fuerza mucho mayor que la del viento, así que el ángulo sigue siendo de casi 30.
6
Resume el vector resultante. Para explicar el vector resultante, deberás indicar tanto su ángulo como magnitud. En este ejemplo con la pelota de golf, el vector resultante tiene una magnitud de 221,81 km/h (137,83 mph) y un ángulo de 27,32 grados por encima de la horizontal.

Método 4

Método 4 de 4:
Revisar los vectores y sus componentes

1
Recuerda la definición de un vector. Un vector es una herramienta matemática que se utiliza en física para representar la forma en que las fuerzas actúan sobre un objeto. Se sabe que un vector representa dos elementos de fuerza: su dirección y su magnitud.^{[10]
X
Fuente de investigación}
- Por ejemplo, en el caso de un objeto en movimiento, puedes describir su desplazamiento al indicar la dirección de su recorrido y su velocidad. Por ejemplo, supongamos que un avión se mueve hacia el noroeste a 805 km/h (500 mph). El noroeste es la dirección mientras que los 805 km/h (500 mph) es la magnitud.
- Un perro jalado por una correa experimenta una fuerza vectorial. Cuando el dueño jala la correa lo hace en dirección diagonal ascendente con una cierta fuerza. El ángulo de dicha diagonal es la dirección del vector, mientras que la intensidad de la fuerza es la magnitud.
2
Entiende la terminología del gráfico de vectores. Al momento de dibujar un vector, ya sea mediante una representación dibujada con exactitud en un papel cuadriculado o simplemente un gráfico aproximado, deberás utilizar algunos términos geométricos.^{[11]
X
Fuente de investigación}
- Un vector está representado gráficamente por medio de un ${\text{rayo}}$ . En geometría, un rayo es un segmento de línea que comienza en un punto y, en teoría, continúa de manera infinita en una dirección. Para dibujarlo, es necesario marcar un punto y luego trazar un segmento de línea de la longitud adecuada, para finalmente hacer una punta de flecha en el extremo opuesto de dicho segmento.
- La ${\text{cola}}$ de un vector es su punto de partida. En geometría, este es el punto final del rayo.
- La ${\text{cabeza}}$ de un vector es la posición en la punta de flecha. La única diferencia importante entre un rayo geométrico y un vector es que, en el primero, la punta de flecha representa el recorrido teórico en una determinada dirección por una distancia infinita. Por otro lado, un vector utiliza las puntas de flecha para indicar la dirección, aunque su longitud termina en la punta del segmento de línea, con la finalidad de medir su magnitud. Esto significa que, en un rayo geométrico, la longitud es irrelevante; mientras que, en un vector, esta es muy importante.
3
Recuerda un poco de trigonometría básica. Los componentes de un vector se basan en la trigonometría de los triángulos rectángulos. Cualquier segmento de línea diagonal puede convertirse en la hipotenusa de un triángulo rectángulo al trazar una línea horizontal desde un extremo y una línea vertical desde el otro. Cuando ambas líneas se conectan, tendrás un triángulo rectángulo.^{[12]
X
Fuente de investigación}
- El ángulo referencial es aquel creado al medir desde la base horizontal del triángulo rectángulo hasta la hipotenusa.
- Para determinar el seno del ángulo referencial, divide la longitud de la pata opuesta entre la de la hipotenusa.
- Para determinar el coseno del ángulo referencial, divide la longitud de la base del triángulo (o la pata adyacente) entre la longitud de la hipotenusa.

Advertencias

Un método útil y rápido para aproximar los componentes vectoriales es medirlos mediante gráficos. No obstante, ten en cuenta que este método no es muy preciso, a menos que seas muy bueno en la gráfica y medición. Si quieres obtener números redondeados rápidamente, entonces este método debería ser suficiente. Por el contrario, para lograr resultados más precisos, utiliza cálculos trigonométricos.