Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 42 748 veces.
El área de la superficie de un cono es la suma del área de la superficie lateral y el de la superficie de la base. Si sabes el radio de la base y la generatriz del cono, puedes encontrar fácilmente el área total de la superficie con una fórmula estándar. Sin embargo, a veces puedes tener el radio y alguna otra medida, como la altura o el volumen del cono. En esos casos, puedes usar el teorema de Pitágoras y la fórmula del volumen para obtener la generatriz y así el área de la superficie del cono.
Pasos
Método 1
Método 1 de 3:Si sabes el radio y la generatriz
-
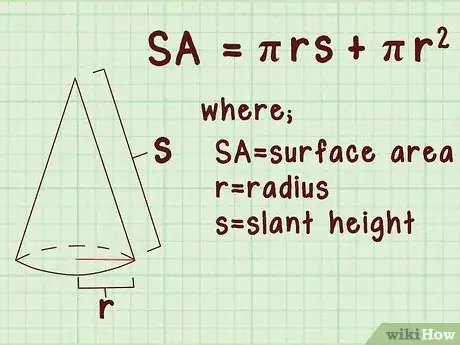
1Establece la fórmula para el área de la superficie del cono. La fórmula , donde equivale al área de la superficie del cono, equivale a la longitud del radio de la base del cono, y equivale a la generatriz del cono.[1]
- El área de la superficie de un cono equivale a la suma del área de la superficie lateral () y al área de la base (), ya que la base de un cono es un círculo.
- La generatriz es la distancia diagonal desde el vértice superior del cono hasta el borde la base.[2]
- Asegúrate de no confundir la “generatriz” con la “altura”, que es la distancia perpendicular entre el vértice superior hasta la base.[3]
-
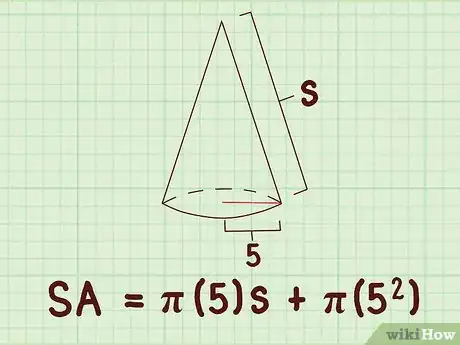
2Agrega el valor del radio en la fórmula. Te deben dar esta longitud o debes ser capaz de medirla. Asegúrate de sustituir ambas variables en la fórmula.
- Por ejemplo, si el radio de la base de un cono es 5 cm, la fórmula lucirá de la siguiente manera: .
-
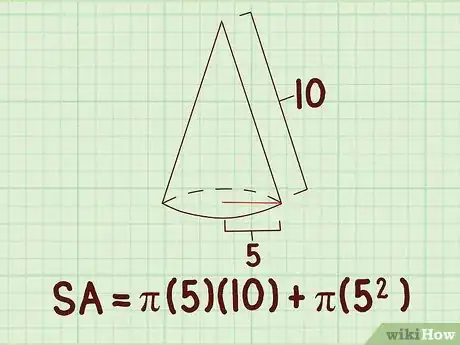
3Agrega el valor de la generatriz a la fórmula. Te deben dar esta longitud o debes ser capaz de medirla.
- Por ejemplo, si la generatriz de un cono es 10 cm, la fórmula lucirá de la siguiente manera: .
-
4Calcular el área de la superficie lateral del cono (). Para hacerlo, multiplica el radio, la generatriz y . Si no usas una calculadora, utiliza 3,14 como el valor de .
- Por ejemplo:
- Por ejemplo:
-
5Calcular el área de la base del cono (). Para hacerlo, eleva al cuadrado el radio de la base, después multiplica por . Si no usas una calculadora, usa 3,14 como el valor de .
- Por ejemplo:
.
- Por ejemplo:
-
6Agrega el área de la superficie lateral y el área de la base del cono. Esto te dará el área total de la superficie del cono en unidades cuadradas.
- Por ejemplo:
De esta forma, el área de la superficie de un cono con un radio de 5 cm y una generatriz de 10 cm es 235,5 centímetros cuadrados.
- Por ejemplo:
Método 2
Método 2 de 3:Si sabes el radio y la altura perpendicular
-
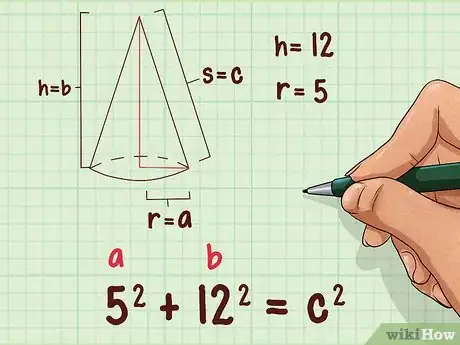
1Establece la fórmula para el teorema de Pitágoras. La fórmula es , donde y equivalen a las alturas de los lados de un triángulo rectángulo, y equivale a la altura de la hipotenusa (el lado opuesto al ángulo recto).[4]
-
2Agrega la longitud del radio y la altura a la fórmula. Usarás el radio y la altura del cono como los dos lados de un triángulo rectángulo. Reemplaza la variable por el radio y la variable por la altura.
- Por ejemplo, si la radio de un cono es 5 cm y la altura es 12 cm, tu fórmula lucirá de la siguiente manera: .
-
3Eleva al cuadrado las longitudes del radio y de la altura, después suma. Recuerda que elevar al cuadrado un número significa multiplicarlo por sí mismo.
- Por ejemplo:
- Por ejemplo:
-
4Toma la raíz cuadrada de cada lado de la ecuación. Esto te dará la longitud de la hipotenusa del triángulo rectángulo, lo que equivale a la generatriz del cono.[7]
- Por ejemplo:
De esta manera, la generatriz del cono es 13 cm.
- Por ejemplo:
-
5Establece la fórmula para el área de la superficie del cono. La fórmula es , donde equivale al área de la superficie del cono, equivale a la longitud del radio de la base del cono, y equivale a la generatriz del cono.[8]
- El área total de la superficie de un cono es igual a la suma del área de la superficie lateral () y del área de la base (, ya que la base de un cono es un círculo).
-
6Agrega todos los valores conocidos a la fórmula. Te deben dar el radio y ya haber calculado la generatriz. Asegúrate de usar la generatriz en la fórmula del área de la superficie, no la altura (perpendicular). Si no usas una calculadora, usa 3,14 para .
- Por ejemplo, para un cono con un radio de 5 cm y una generatriz de 13 cm, la fórmula lucirá de la siguiente manera: .
-
7Multiplica para encontrar el área lateral y el área de la base. Después, suma todos estos productos. La suma te dará el área total de la superficie del cono en unidades cuadradas.
- Por ejemplo:
De esta manera, el área de la superficie de un cono con un radio de 5 cm y una altura de 12 cm es 282,6 centímetros cuadrados.
- Por ejemplo:
Método 3
Método 3 de 3:Si sabes el radio y el volumen
-
1Establece la fórmula para el volumen de un cono. La fórmula es , donde equivale al volumen del cono, equivale al radio de la base del cono, y equivale a la altura perpendicular del cono.[9]
-
2Agrega los valores conocidos a la fórmula. Debes saber el volumen y la longitud del radio. Si no los sabes, no puedes usar este método. Si no usas una calculadora, utiliza 3,14 para .
- Por ejemplo, si sabes que un cono tiene un volumen de 950 centímetros cúbicos y un radio de 6 cm, la fórmula lucirá de la siguiente manera: .
-
3Completa la multiplicación. Primero, eleva al cuadrado el radio, después multiplica ese valor por . Después, multiplica ese producto por . Esto te dará el coeficiente para la variable .
- Por ejemplo:
- Por ejemplo:
-
4Divide cada lado entre el coeficiente . Esto te dará la valor de , que es la altura perpendicular del cono. Necesitarás esta información para encontrar la generatriz del cono, que se necesita saber al momento de resolver el área de la superficie.
- Por ejemplo:
De esta manera, la altura del cono es 25,21 cm.
- Por ejemplo:
-
5Establece la fórmula para el teorema de Pitágoras. La fórmula es , donde y equivalen a las longitudes de los lados de un triángulo recto, y equivale a la longitud de la hipotenusa (el lado opuesto al ángulo recto).[12]
-
6Agrega la longitud del radio y la altura a la fórmula. Usarás el radio y la altura del cono como los dos lados de un triángulo recto. Reemplaza la variable por el radio y la variable por la altura.
- Por ejemplo: si el radio de un cono es 6 cm y la altura es 25,21 cm, la fórmula lucirá de la siguiente manera: .
-
7Calcula . Esto te dará la longitud de la hipotenusa del triángulo recto, que también es la generatriz del cono.
- Por ejemplo:
De esta manera, la generatriz del cono es 25,91 cm.
- Por ejemplo:
-
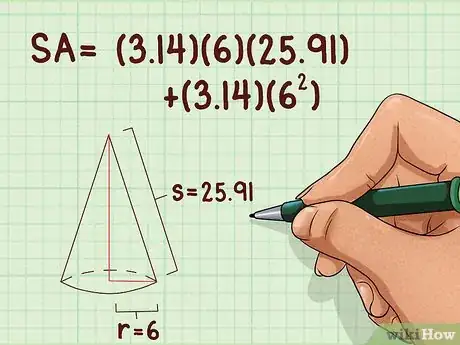
8Establece la fórmula para el área de la superficie del cono. La fórmula es , donde equivale al área de la superfície del cono, equivale a la altura del radio de la base del cono, y equivale a la generatriz del cono.[13]
- El área total de la superficie de un cono es igual a la suma del área de la superficie lateral () y el área de la base (, ya que la base de un cono es un círculo).
-
9Agrega todos los valores conocidos a la fórmula. Asegúrate de usar la generatriz en la fórmula del área de la superficie, no la altura (perpendicular). Si no usas una calculadora, utiliza 3,14 para .
- Por ejemplo, para un cono con un radio de 6 cm y una generatriz de 25,91 cm, la fórmula lucirá de la siguiente manera: .
-
10Multiplica para encontrar el área lateral y el área de la base. Después, suma todos estos productos. La suma te dará el área total de la superficie del cono en unidades cuadradas.
- Por ejemplo:
De esta manera, el área de la superficie de un cono con un radio de 6 cm y un volume de 950 centímetros cúbicos es 601,18 centímetros cuadrados.
- Por ejemplo:
Consejos
- El teorema de Pitágoras utiliza al radio, la altura perpendicular y a la generatriz, donde la generatriz actúa como la hipotenusa: 2(radio) + 2(altura perpendicular) = 2(generatriz).
Referencias
- ↑ http://www.mathopenref.com/conearea.html
- ↑ http://www.mathwords.com/s/slant_height.htm
- ↑ http://www.mathopenref.com/cone.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathwords.com/s/slant_height.htm
- ↑ http://www.mathopenref.com/cone.html
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_VolumeSurfaceAreaCones.xml
- ↑ http://www.mathopenref.com/conearea.html
- ↑ http://www.mathopenref.com/conevolume.html




















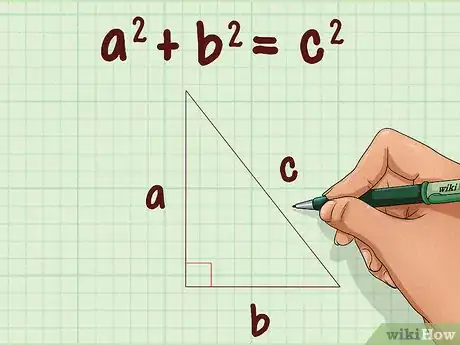





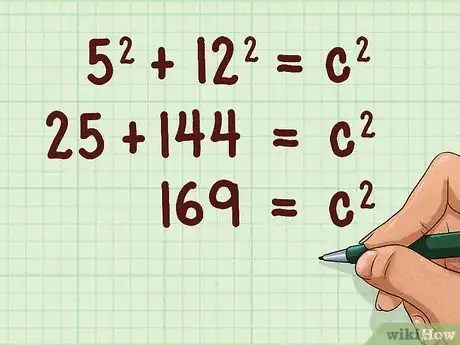


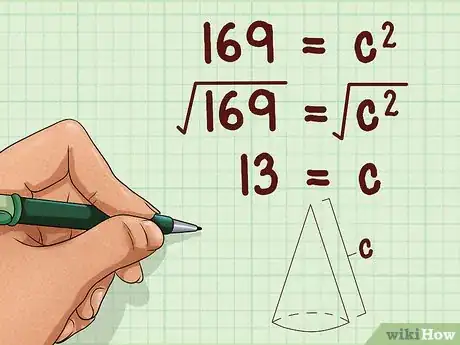





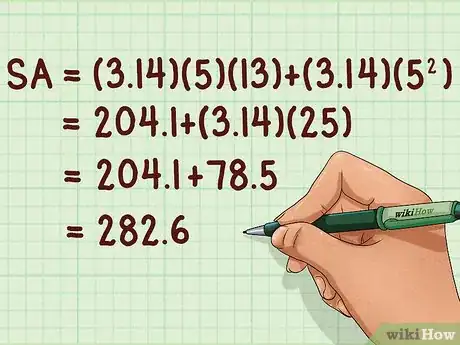







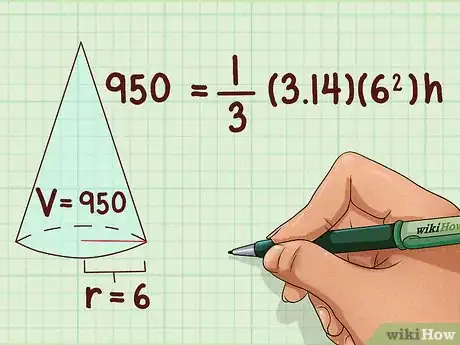









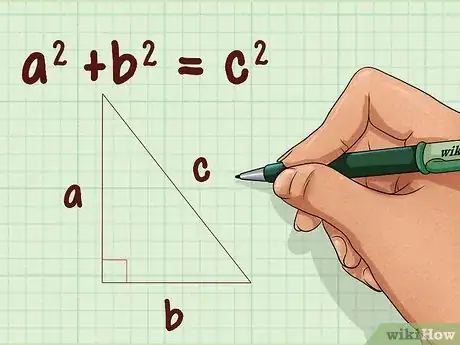
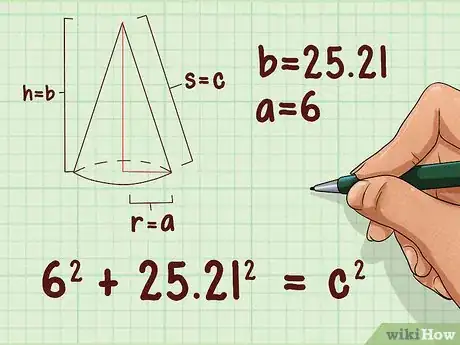

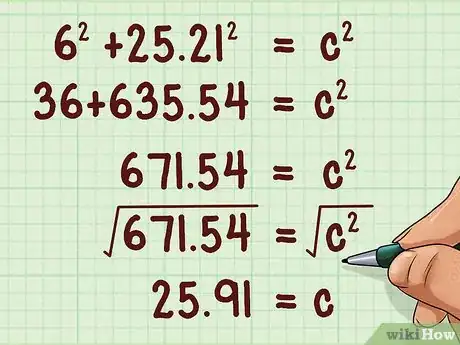






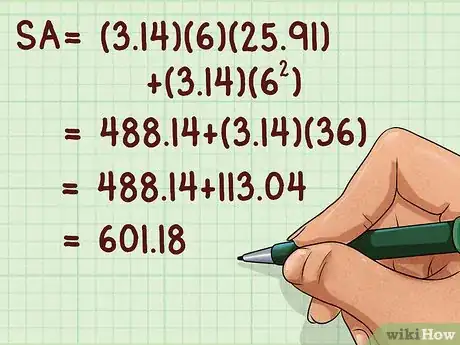






















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 42 748 veces.