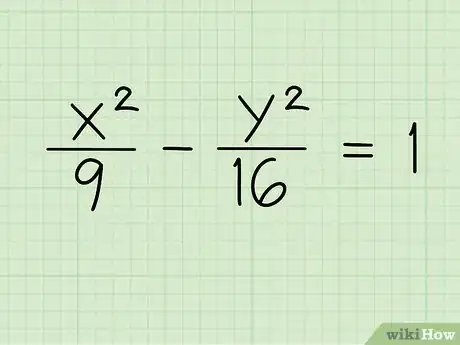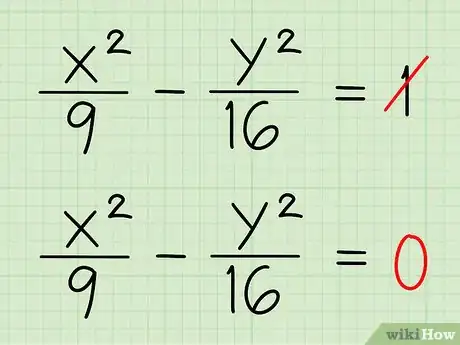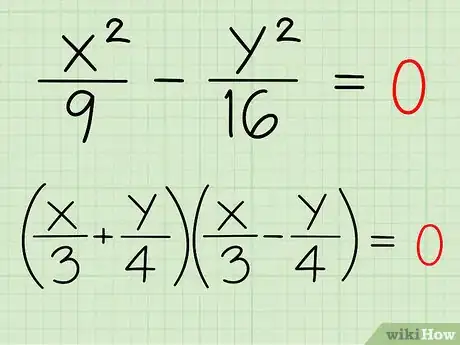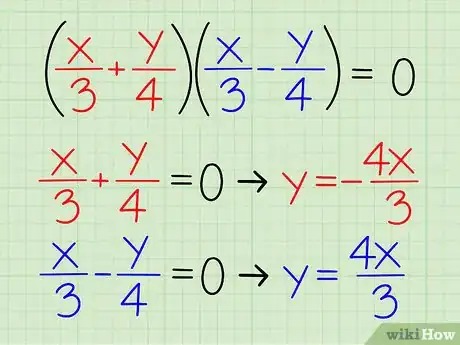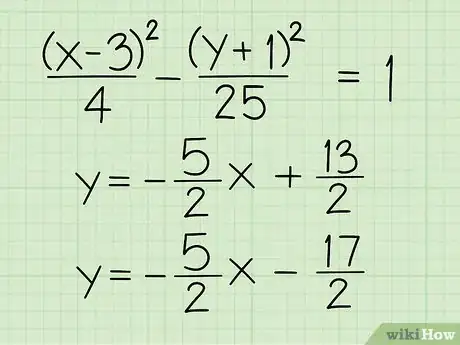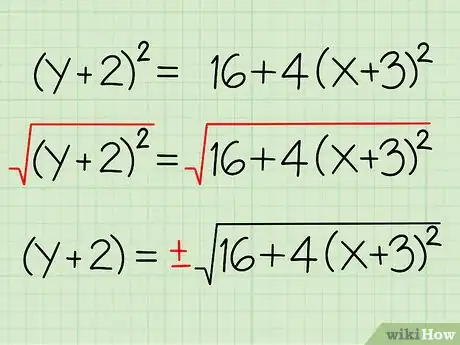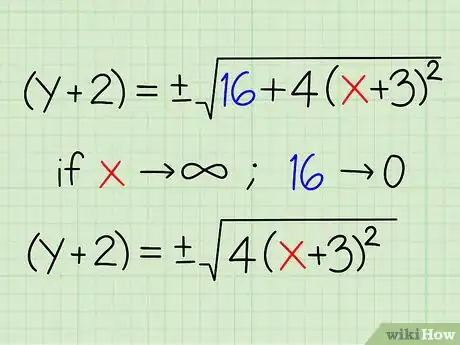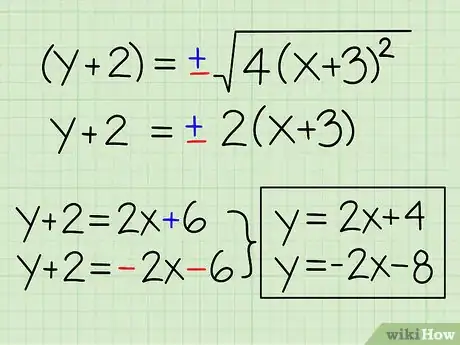Cómo encontrar las ecuaciones de las asíntotas de una hipérbola

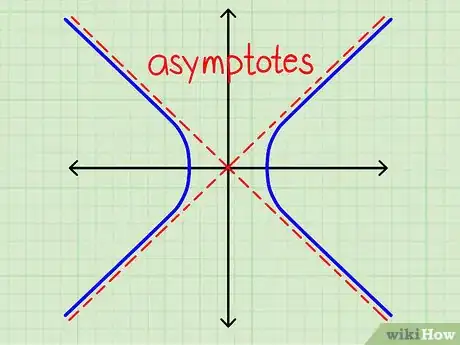
Las asíntotas de una hipérbola son las líneas que pasan por su centro. La hipérbola puede acercarse más y más a las asíntotas, pero nunca puede llegar a tocarlas. Hay dos formas distintas de hallar las asíntotas de una hipérbola. Aprendiendo ambos métodos podrás comprender mejor el concepto.

Método 1
Método 1 de 2:
Factorizar

  1. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 1
    1
    Anota la ecuación de la hipérbola en su fórmula estándar. Empezaremos con un sencillo ejemplo: una hipérbola con el centro de su origen. Para estas hipérbolas, la fórmula estándar de la ecuación es x2/a2 - y2/b2 = 1 en el caso de las hipérbolas que se extienden a la izquierda y a la derecha, o y2/b2 - x2/a2 = 1 en el caso de las hipérbolas que se extienden hacia arriba y hacia abajo.[1] Recuerda que x e y son variables, mientras que a y b son constantes (números ordinarios).
    • Ejemplo 1: x2/9 - y2/16 = 1
    • En los libros de texto y apuntes de algunos profesores, las posiciones de a y b aparecen cambiadas en estas mismas ecuaciones.[2] Analiza la ecuación al detalle para comprender lo que pasa. Si simplemente memorizas las ecuaciones, no sabrás resolverlas cuando te encuentres anotaciones distintas.
  2. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 2
    2
    Iguala la ecuación a cero en vez de a uno. Esta nueva ecuación representará a ambas asíntotas. Sin embargo, será un poco más difícil separar una de otra.[3]
    • Ejemplo 1: x2/9 - y2/16 = 0
  3. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 3
    3
    Factoriza la nueva ecuación. Factoriza la parte de la izquierda de la ecuación en dos productos. Refresca la memoria para factorizar ecuaciones cuadráticas si lo necesitas, o sigue las instrucciones mientras continuamos con el Ejemplo 1:
    • Acabaremos obteniendo la ecuación (__ ± __)(__ ± __) = 0.
    • Los dos primeros términos se deben multiplicar entre sí para obtener x2/9, así que haz la raíz cuadrada y escríbela en ese espacio: (x/3 ± __)(x/3 ± __) = 0
    • De la misma forma, haz la raíz cuadrada de y2/16 y escríbela en los espacios restantes: (x/3 ± y/4)(x/3 ± y/4) = 0
    • Dado que no hay más términos, escribe un sígno de suma y otro de resta, de forma que los demás términos se cancelen al hacer la multiplicación: (x/3 + y/4)(x/3 - y/4) = 0
  4. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 4
    4
    Separa los factores y halla y. Para obtener las ecuaciones de las asíntotas, separa los dos factores y despeja la y.
    • Ejemplo 1: Dado que (x/3 + y/4)(x/3 - y/4) = 0, we know x/3 + y/4 = 0 and x/3 - y/4 = 0
    • Reescribe x/3 + y/4 = 0 → y/4 = - x/3 → y = - 4x/3
    • Reescribe x/3 - y/4 = 0 → - y/4 = - x/3 → y = 4x/3
  5. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 5
    5
    Prueba el mismo proceso con una ecuación más complicada. Acabamos de hallar las asíntotas de una hipérbola centrada en el origen. La ecuación de una hipérbola centrada en (h, k) se escribe con la fórmula (x - h)2/a2 - (y - k)2/b2 = 1, o (y - k)2/b2 - (x - h)2/a2 = 1. Puedes resolverlas con el mismo método de factorización anteriormente descrito. Solo tienes que dejar los términos de (x - h) y (y - k) intactos hasta el último paso.
    • Ejemplo 2: (x - 3)2/4 - (y + 1)2/25 = 1
    • Iguala la ecuación a cero para obtener:
    • ((x - 3)/2 + (y + 1)/5)((x - 3)/2 - (y + 1)/5) = 0
    • Separa cada factor y resuélvelos para hallar las ecuaciones de las asíntotas:
    • (x - 3)/2 + (y + 1)/5 = 0 → y = -5/2x + 13/2
    • ((x - 3)/2 - (y + 1)/5) = 0 → y = 5/2x - 17/2
    Anuncio

Método 2
Método 2 de 2:
Despejar la Y

  1. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 6
    1
    Escribe la ecuación de la hipérbola con el término de y2 a la izquierda. Este método es muy útil si tienes una ecuación en su fórmula cuadrática general. Aunque esté escrita en su forma estándar para hipérbolas, este acercamiento puede ayudarte a comprender mejor la naturaleza de las asíntotas. Reordena la ecuación de forma que el término de y2 o (y - k)2 esté a un lado para empezar.
    • Ejemplo 3: (y + 2)2/16 - (x + 3)2/4 = 1
    • Suma el término de x a ambos lados y, después, multiplica a cada lado por 16:
    • (y + 2)2 = 16(1 + (x + 3)2/4)
    • Simplifica:
    • (y + 2)2 = 16 + 4(x + 3)2
  2. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 7
    2
    Haz la raíz cuadrada a cada lado. Haz la raíz cuadrada, pero no intentes simplificar el lado derecho aún. Recuerda que cuando hagas la raíz cuadrada, habrá dos soluciones posibles: una positiva y otra negativa. Por ejemplo, -2 * -2 = 4, so √4 puede ser igual a -2 y a 2.) Utiliza el signo de "+ o -" (±) para hacer el seguimiento de ambas soluciones.
    • √((y + 2)2) = √(16 + 4(x + 3)2)
    • (y+2) = ± √(16 + 4(x + 3)2)
  3. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 8
    3
    Revisa la definición de una asíntota. Es importante que comprendas esto antes de continuar con el siguiente paso. La asíntota de una hipérbola es una línea a la que la hipérbola se acerca más y más conforme x aumenta. X nunca llegará a tocar a la asíntota, pero si prolongamos la hipérbola con valores cada vez mayores de x, nos iremos acercando más y más a la asíntota.
  4. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 9
    4
    Ajusta la ecuación para valores grandes de x. Dado que estamos intentando hallar la ecuación de la asíntota, solo nos preocuparemos de x para valores muy grandes (con la intención de "acercarnos al infinito"). De esta forma, podremos ignorar ciertas constantes de la ecuación, ya que suponen una parte mínima en relación con el término de x. Una vez que x llegue a 99 billones (por ejemplo), sumar tres supone un cambio tan insignificante que podemos ignorarlo.
    • En la ecuación (y+2) = ± √(16 + 4(x + 3)2), conforme x se acerca a infinito, el 16 pierde relevancia.
    • (y+2) = aproximadamente ± √(4(x + 3)2) para valores grandes de x.
  5. Imagen titulada Find the Equations of the Asymptotes of a Hyperbola Step 10
    5
    Despeja y para hallar las dos ecuaciones de la asíntota. Ahora que nos hemos deshecho de la constante, podemos simplificar la raíz cuadrada. Despeja los términos de y para obtener el resultado. Recuerda que debes dividir el símbolo ± en dos ecuaciones separadas, una con + y otra con -.
    • y + 2 = ±√(4(x+3)^2)
    • y + 2 = ±2(x+3)
    • y + 2 = 2x + 6 and y + 2 = -2x - 6
    • y = 2x + 4 and y = -2x - 8
    Anuncio

Consejos

  • Recuerda que la ecuación de una hipérbola y su par de asíntotas siempre difieren en una constante.
  • Para operar con hipérbolas rectangulares, primero conviértelas a la forma estándar y, después, halla las asíntotas.
  • Una hipérbola rectangular es aquella en la que a = b= constante = c.
Anuncio

Advertencias

  • Ten cuidado de escribir las ecuaciones siempre con la fórmula estándar.
Anuncio

wikiHows relacionados

calcular el radio de un círculo
Cómo
calcular el radio de un círculo
calcular la circunferencia de un círculo
Cómo
calcular la circunferencia de un círculo
encontrar el vértice de una ecuación cuadrática
Cómo
encontrar el vértice de una ecuación cuadrática
sacar el área de un cuadrilátero
Cómo
sacar el área de un cuadrilátero
calcular ángulos
Cómo
calcular ángulos
calcular la circunferencia
Cómo
calcular la circunferencia
encontrar el radio de una esfera
Cómo
encontrar el radio de una esfera
sacar el volumen de un cubo
Cómo
sacar el volumen de un cubo
encontrar la magnitud de un vector
Cómo
encontrar la magnitud de un vector
calcular cuántas diagonales tiene un polígono
Cómo
calcular cuántas diagonales tiene un polígono
medir un ángulo sin usar un transportador
Cómo
medir un ángulo sin usar un transportador
sacar el angulo de un triangulo
Cómo
sacar el angulo de un triangulo
dibujar un hexágono
Cómo
dibujar un hexágono
calcular metros cuadrados
Cómo
calcular metros cuadrados
Anuncio

Referencias

  1. ↑ http://www.purplemath.com/modules/hyperbola.htm
  2. ↑ https://www.khanacademy.org/math/algebra2/conics_precalc/hyperbolas-precalc/
  3. ↑ https://books.google.com/books?id=MBAwrjc3gqMC&sitesec=buy&source=gbs_vpt_read

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 12 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 39 477 veces.
Categorías: Geometría
Anuncio