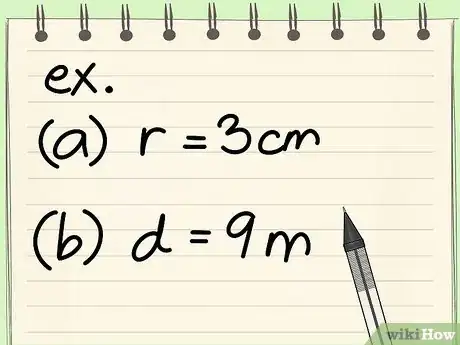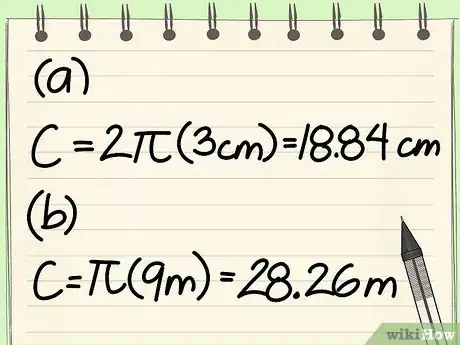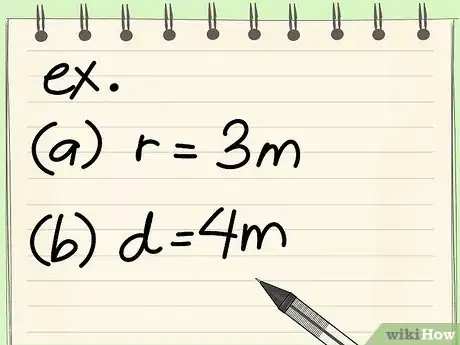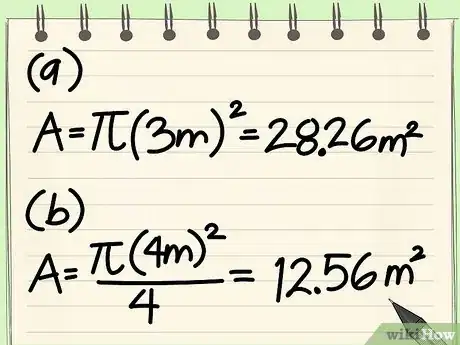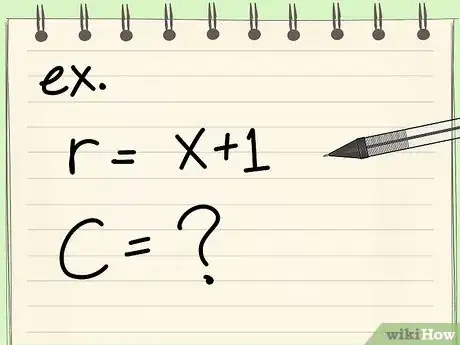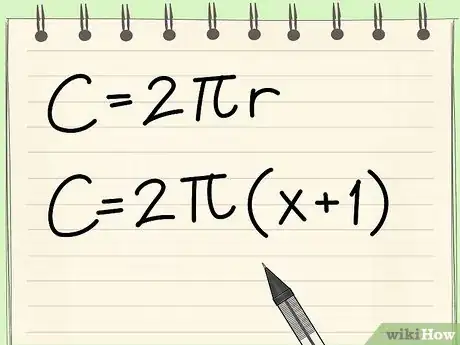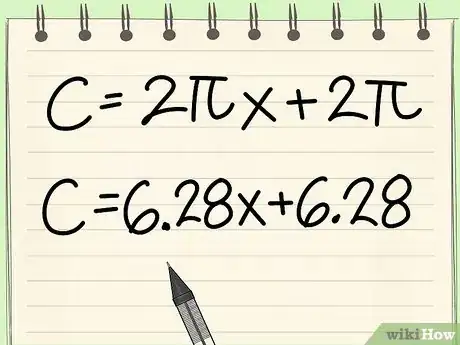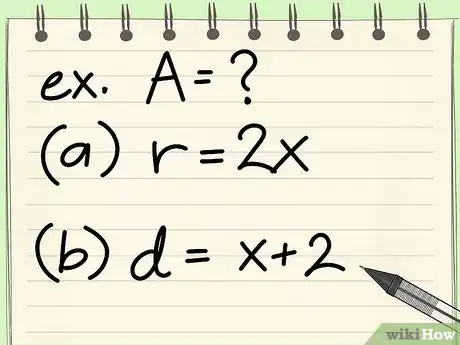Cómo hallar la circunferencia y el área o superficie de un círculo

Un círculo es una línea bidimensional que forma una vuelta cerrada en donde todos los puntos están a la misma distancia del centro.[1] La circunferencia (C) de un círculo es su perímetro, o la distancia alrededor de él.[2] El área (A) de un círculo es la cantidad de espacio que ocupa el círculo o la región contenida dentro de él.[3] Tanto el área como el perímetro pueden calcularse con fórmulas simples usando el radio o el diámetro del círculo y el valor de pi.

Parte 1
Parte 1 de 3:
Calcular la circunferencia

  1. Imagen titulada Find the Circumference and Area of a Circle Step 1
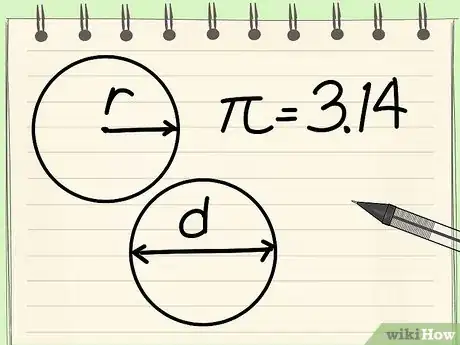
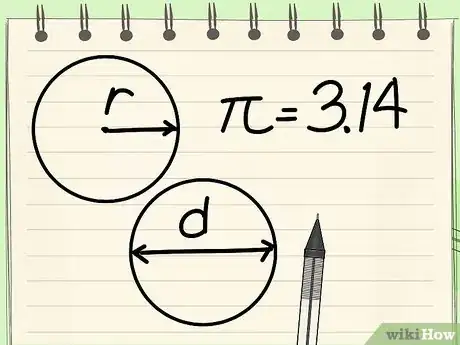
    1
    Aprende la fórmula para la circunferencia. Existen dos fórmulas que pueden usarse para calcular la circunferencia de un círculo: C = 2πr o C = πd, donde π es la constante matemática igual a aproximadamente 3,14,[4] r es igual al radio y d es igual al diámetro.[5]
    • Debido a que el radio de un círculo es igual a dos veces su diámetro, estas ecuaciones son esencialmente iguales.
    • Las unidades para la circunferencia pueden ser cualquier unidad para medir la longitud: pies, millas, metros, centímetros, etc.
  2. Imagen titulada Find the Circumference and Area of a Circle Step 2
    2
    Comprende las diferentes partes de la fórmula. Existen tres componentes para encontrar la circunferencia de un círculo: el radio, el diámetro y π. El radio y el diámetro están relacionados: el radio es igual a la mitad del diámetro mientras que el diámetro es igual al doble del radio.
    • El radio (r) de un círculo es la distancia de un punto en el círculo hasta el centro del círculo.
    • El diámetro (d) de un círculo es la distancia de un punto en el círculo hasta otro punto directamente opuesto a él pasando por el centro del círculo.[6]
    • La letra griega pi (π) representa la proporción entre la circunferencia y el diámetro y está representada por el número 3,14159265…, un número irracional que no tiene ni un dígito final ni un patrón reconocible de repetición de dígitos.[7] Este número comúnmente se redondea a 3,14 para cálculos básicos.
  3. Imagen titulada Find the Circumference and Area of a Circle Step 3
    3
    Mide el radio o el diámetro del círculo. Usando una regla, coloca un extremo a un lado del círculo y atraviesa el punto central hasta el otro lado del círculo. La distancia hasta el centro del círculo es el radio mientras que la distancia hasta el otro extremo del círculo es el diámetro.
    • En la mayoría de los problemas de matemáticas de los libros de texto, se te dará el radio o el diámetro.
  4. Imagen titulada Find the Circumference and Area of a Circle Step 4
    4
    Reemplaza las variables y resuelve. Una vez que hayas determinado el radio o el diámetro del círculo, puedes reemplazar estas variables en la ecuación adecuada. Si tienes el radio, usa C = 2πr y, si tienes el diámetro, usa C = πd.
    • Por ejemplo: ¿cuál es la circunferencia de un círculo con un radio de 3 cm?
      • Escribe la fórmula: C = 2πr
      • Reemplaza las variables: C = 2π3
      • Multiplica: C = (2*3*π) = 6π = 18,84 cm
    • Por ejemplo: ¿cuál es la circunferencia de un círculo con un diámetro de 9 m?
      • Escribe la fórmula: C = πd
      • Reemplaza las variables: C = 9π
      • Multiplica: C = (9*π) = 28,26 m
  5. Imagen titulada Find the Circumference and Area of a Circle Step 5
    5
    Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es momento de practicar con algunos ejemplos. Mientras más problemas resuelvas, te será más fácil hacerlo en el futuro.
    • Encuentra la circunferencia de un círculo de un diámetro de 1,5 m (5 pies).
      • C = πd = 1,5π = 4,71 m (15,7 pies)
    • Encuentra la circunferencia de un círculo con un radio de 3 m (10 pies).
      • C = 2πr = C = 2π3 = 2 * 3 * π = 18,84 m (62,8 pies).

Parte 2
Parte 2 de 3:
Calcular el área

  1. Imagen titulada Find the Circumference and Area of a Circle Step 6
    1
    Aprende la fórmula para el área de un círculo. El área de un círculo puede calcularse usando el diámetro o el radio con dos fórmulas diferentes: A = πr2 o A = π(d/2)2,[8] donde π es la constante matemática aproximadamente igual a 3,14,[9] r es igual al radio y d es el diámetro.
    • Debido a que el radio de un círculo es igual a dos veces su diámetro, estas ecuaciones son esencialmente iguales.
    • Las unidades para el área pueden ser cualquier unidad para medir la longitud al cuadrado: metros cuadrados (m2), centímetros cuadrados (cm2), pies cuadrados, etc.
  2. Imagen titulada Find the Circumference and Area of a Circle Step 7
    2
    Comprende las diferentes partes de la fórmula. Hay tres componentes para encontrar la circunferencia de un círculo: el radio, el diámetro y π. El radio y el diámetro están relacionados: el radio es igual a la mitad del diámetro mientras que el diámetro es igual al doble del radio.
    • El radio (r) de un círculo es la distancia desde un punto del círculo hasta el centro del círculo.
    • El diámetro (d) de un círculo es la distancia desde un punto del círculo hasta otro directamente opuesto a él pasando por el centro del círculo.[10]
    • La letra griega pi (π) representa la proporción entre la circunferencia y el diámetro y está representada por el número 3,14159265…, un número irracional que no tiene ni un dígito final ni un patrón reconocible de repetición de dígitos.[11] Este número comúnmente se redondea a 3,14 para cálculos básicos.
  3. Imagen titulada Find the Circumference and Area of a Circle Step 8
    3
    Mide el radio o el diámetro del círculo. Usando una regla, coloca un extremo a un lado del círculo y atraviesa el punto central hasta el otro lado del círculo. La distancia hasta el centro del círculo es el radio, mientras que la distancia hasta el otro extremo del círculo es el diámetro.
    • En la mayoría de los problemas de matemáticas de los libros de texto, se te dará el radio o el diámetro.
  4. Imagen titulada Find the Circumference and Area of a Circle Step 9
    4
    Reemplaza las variables y resuelve. Una vez que hayas determinado el radio o el diámetro del círculo, puedes reemplazar estas variables en la ecuación adecuada. Si tienes el radio, usa A = πr2 y, si tienes el diámetro, usa A = π(d/2)2.
    • Por ejemplo: ¿cuál es el área de un círculo con un radio de 3 m?
      • Escribe la fórmula: A = πr2
      • Reemplaza las variables: A = π32
      • Eleva el radio al cuadrado: r2 = 32 = 9
      • Multiplica por pi: A = 9π = 28,26 m2
    • Por ejemplo: ¿cuál es el área de un círculo con un diámetro de 4 m?
      • Escribe la fórmula: A = π(d/2)2
      • Reemplaza las variables: A = π(4/2)2
      • Divide el diámetro entre 2: d/2 = 4/2 = 2
      • Eleva el resultado al cuadrado: 22 = 4
      • Multiplica por pi: A = 4π = 12,56 m2
  5. Imagen titulada Find the Circumference and Area of a Circle Step 10
    5
    Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es momento de practicar con algunos ejemplos. Mientras más problemas resuelvas, te será más fácil hacerlo en el futuro.
    • Encuentra el área de un círculo con un diámetro de 2 m (7 pies).
      • A = π(d/2)2 = π(2/2)2 = π(1)2 = 1 * π = 3,14 m2 (38,47 pies cuadrados).
    • Encuentra el área de un círculo con un radio de 0,9 m (3 pies).
      • A = πr2 = π0,92 = 0,81 * π = 2,54 m2 (28,26 pies cuadrados).

Parte 3
Parte 3 de 3:
Calcular el área y la circunferencia con variables

  1. Imagen titulada Find the Circumference and Area of a Circle Step 11
    1
    Determina el radio o el diámetro del círculo. Algunos problemas pueden darte un radio o diámetro que tenga una variable, por ejemplo: r = (x + 7) o d = (x + 3). En este caso, de todas formas puedes encontrar el área o la circunferencia pero tu respuesta final también tendrá esa variable. Escribe el radio o el diámetro como figuran en el problema.
    • Por ejemplo: calcula la circunferencia de un círculo con un radio de (x = 1).
  2. Imagen titulada Find the Circumference and Area of a Circle Step 12
    2
    Escribe la fórmula con la información dada. Ya sea que vayas a encontrar el área o la circunferencia, de todas formas seguirás los pasos básicos de reemplazar lo que sepas en la ecuación. Escribe la fórmula para el área o la circunferencia y luego escribe las variables dadas.
    • Por ejemplo: calcula la circunferencia de un círculo con un radio de (x + 1).
    • Escribe la fórmula: C = 2πr
    • Reemplaza la información dada: C = 2π(x+1)
  3. Imagen titulada Find the Circumference and Area of a Circle Step 13
    3
    Resuelve como si la variable fuera un número. Para este punto, puedes simplemente resolver el problema como normalmente lo harías, tratando a la variable como si fuera cualquier otro número. Es posible que tengas que usar la propiedad distributiva para simplificar la respuesta final.
    • Por ejemplo: calcula la circunferencia de un círculo con un radio de (x + 1).
    • C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28
    • Si se te da el valor de x más adelante en el problema, puedes reemplazarlo y obtener una respuesta con un número entero.
  4. Imagen titulada Find the Circumference and Area of a Circle Step 14
    4
    Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es momento de practicar con algunos ejemplos. Mientras más problemas resuelvas, te será más fácil hacerlo en el futuro.
    • Encuentra el área de un círculo con un radio de 2x.
      • A = πr2 = π(2x)2 = π4x2 = 12,56x2
    • Encuentra el área de un círculo con un diámetro de (x + 2).
      • A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π

wikiHows relacionados

calcular el radio de un círculo
Cómo
calcular el radio de un círculo
calcular la circunferencia de un círculo
Cómo
calcular la circunferencia de un círculo
encontrar el vértice de una ecuación cuadrática
Cómo
encontrar el vértice de una ecuación cuadrática
sacar el área de un cuadrilátero
Cómo
sacar el área de un cuadrilátero
calcular ángulos
Cómo
calcular ángulos
calcular la circunferencia
Cómo
calcular la circunferencia
encontrar el radio de una esfera
Cómo
encontrar el radio de una esfera
sacar el volumen de un cubo
Cómo
sacar el volumen de un cubo
calcular cuántas diagonales tiene un polígono
Cómo
calcular cuántas diagonales tiene un polígono
encontrar la magnitud de un vector
Cómo
encontrar la magnitud de un vector
medir un ángulo sin usar un transportador
Cómo
medir un ángulo sin usar un transportador
sacar el angulo de un triangulo
Cómo
sacar el angulo de un triangulo
calcular metros cuadrados
Cómo
calcular metros cuadrados
dibujar un hexágono
Cómo
dibujar un hexágono

Referencias

  1. ↑ http://www.mathopenref.com/circle.html
  2. ↑ http://www.mathopenref.com/circumference.html
  3. ↑ http://www.mathopenref.com/circlearea.html
  4. ↑ http://www.mathopenref.com/pi.html
  5. ↑ http://www.mathopenref.com/circumference.html
  6. ↑ http://www.mathopenref.com/diameter.html
  7. ↑ https://www.mathsisfun.com/definitions/pi.html
  8. ↑ http://www.mathgoodies.com/lessons/vol2/circle_area.html
  9. ↑ http://www.mathopenref.com/pi.html
  1. ↑ http://www.mathopenref.com/diameter.html
  2. ↑ https://www.mathsisfun.com/definitions/pi.html

Acerca de este wikiHow

Grace Imson, MA
Coescrito por:
Grace Imson, MA
Instructora de matemáticas en City College de San Francisco
Este artículo fue coescrito por Grace Imson, MA. Grace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis. Este artículo ha sido visto 244 162 veces.
Categorías: Geometría