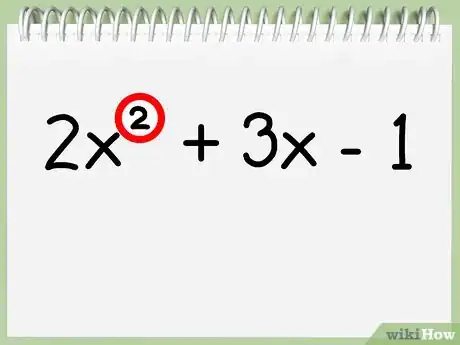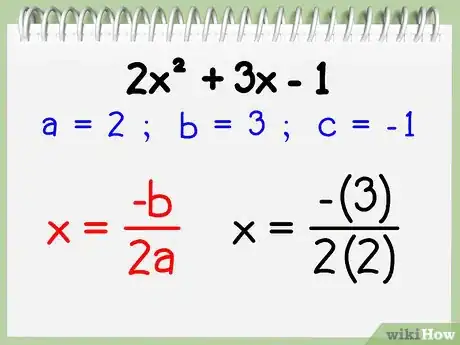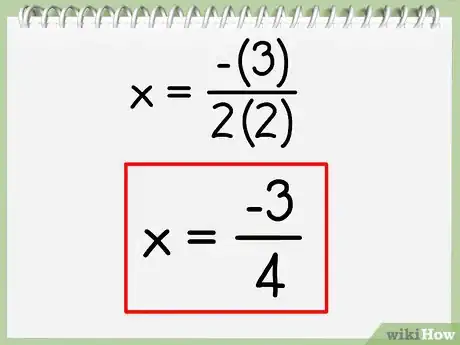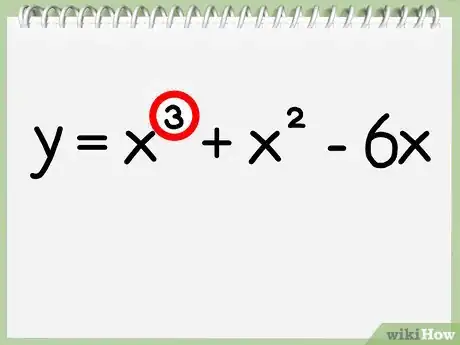Cómo hallar un eje de simetría

Información del autor

La gráfica de un polinomio o una función revela muchas características que no se podrían comprender con claridad sin una representación visual. Una de estas características es el eje de simetría: una línea vertical que divide la gráfica en dos partes simétricamente iguales. Hallar el eje de simetría de un polinomio dado es bastante fácil. Aquí tienes dos métodos básicos.

Método 1

Método 1 de 2:
Encontrar el eje de simetría para polinomios de segundo grado

1
Comprueba el grado del polinomio. El grado de un polinomio se define, sencillamente, por el valor del máximo exponente de la función. Si el grado del polinomio es 2 (no hay ningún exponente mayor que x²), podrás hallar el eje de simetría utilizando este método. Si el grado del polinomio es mayor que 2, utiliza el método 2.
- Para ilustrar el concepto, utiliza como ejemplo el polinomio 2x² + 3x – 1. Su variable de máximo exponente es x², por lo que es un polinomio de segundo grado, y podrás utilizar este método para hallar su eje de simetría.
2
Introduce los valores numéricos en la fórmula del eje de simetría. Para calcular el eje de simetría de un polinomio de segundo grado expresado como ax² + bx +c (una parábola), puedes utilizar la fórmula básica x = -b / 2a.
- Si utilizamos el ejemplo de arriba, a = 2, b = 3, y c = -1. Introduce estos valores en la fórmula para obtener:
  x = -3 / 2(2) = -3/4.
3
Anota la ecuación de los ejes de simetría. El valor calculado con la fórmula del eje de simetría es el punto de corte del eje de simetría con el eje X.
- Siguiendo con el ejemplo, el eje de simetría es -3/4.
Anuncio

Método 2

Método 2 de 2:
Hallar el eje de simetría gráficamente

1
Comprueba el grado del polinomio. El grado de un polinomio se define, simplemente, por el valor del máximo exponente de la función. Si el grado del polinomio es 2 (no hay ningún exponente mayor que x²), puedes hallar el eje de simetría utilizando la fórmula del método anterior. Si el grado del polinomio es mayor que 2, utiliza este método gráfico.
2
Dibuja los ejes X e Y. Traza dos líneas formando un signo de sumar. La línea horizontal es el eje X, y la vertical, el eje Y.
3
Gradúa la gráfica. Marca ambos ejes con números separados por intervalos iguales. Los espacios deben ser uniformes en ambos ejes.
4
Calcula y = f(x) para cada valor de x. Anota el polinomio o la función y calcula los valores de f(x) introduciendo todos los valores de x en la fórmula.
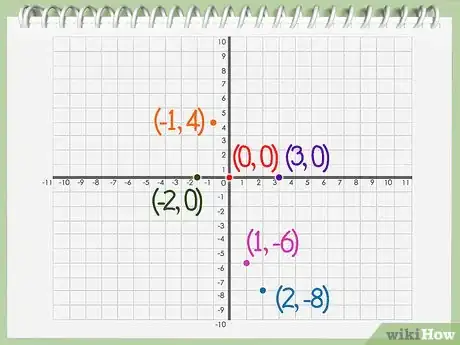
5
Halla un punto en la gráfica a partir de cada par de coordenadas. Ahora tienes pares de y = f(x) por cada valor de x en el eje. Halla un punto en la gráfica a partir de cada par de coordenadas (x, y) y márcalo (cortando verticalmente al eje X y horizontalmente al eje Y).
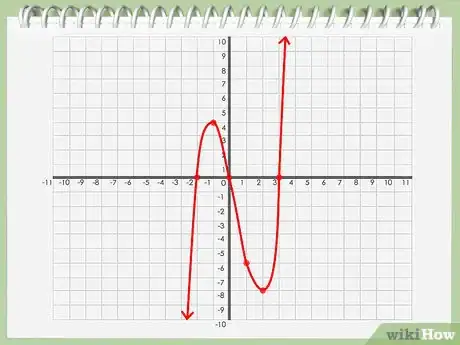
6
Dibuja la gráfica del polinomio. Una vez que hayas marcado todos los puntos de la gráfica, podrás conectarlos trazando una línea continua que será la representación gráfica del polinomio.
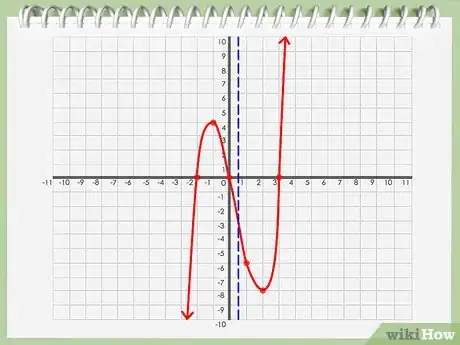
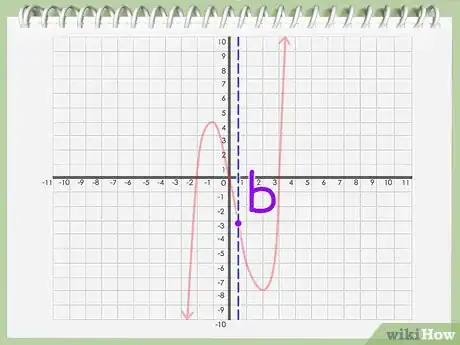
7
Busca el eje de simetría. Analiza la gráfica cuidadosamente. Busca aquel punto por el que puedas trazar una línea dividiendo la gráfica en dos partes simétricamente iguales.
8
Anota el valor del eje de simetría. Si encuentras un punto (llamémoslo "b") en el eje X por el que pase una línea vertical que divida la gráfica en dos mitades simétricamente iguales, entonces ese punto b es el eje de simetría.

Anuncio

Consejos

Tanto el eje X como el Y deben tener una longitud suficiente para poder representar claramente toda la gráfica.
Algunos polinomios no son simétricos. Por ejemplo, y = 3x no tiene eje de simetría.
La simetría de un polinomio se puede clasificar como par o impar. Cualquier gráfica que tenga un eje de simetría respecto al eje y tendrá una simetría par, mientras que toda gráfica que tenga un eje de simetría respecto al eje X tendrá una simetría impar.

Anuncio