Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 31 238 veces.
Puedes medir el largo de una línea vertical u horizontal en un plano de coordenadas contando las coordenadas; sin embargo, medir el largo de una línea diagonal es un poco más complicado. Puedes usar la fórmula de la distancia para encontrar el largo de tal línea. Esta fórmula es básicamente el teorema de Pitágoras, el cual puedes ver si imaginas el segmento de línea dado como la hipotenusa de un triángulo rectángulo.[1] Al usar esta fórmula de geometría tan básica, medir las líneas en un plano de coordenadas se vuelve una tarea muy sencilla.
Pasos
Parte 1
Parte 1 de 2:Establecer la fórmula
-
1Establece la fórmula de la distancia. La fórmula establece que , donde es igual a la distancia de la línea, equivalen a las coordenadas del primer extremo del segmento de línea y equivalen a las coordenadas del segundo extremo del segmento de línea.[2]
-
2Encuentra las coordenadas de los extremos de la línea. Podrías ya tenerlos. De no ser así, cuenta a lo largo del "eje x" y el "eje y" para encontrar las coordenadas.
- El "eje x" es el eje horizontal y el "eje y" es el eje vertical.
- Las coordenadas de un punto se escriben de la siguiente manera .
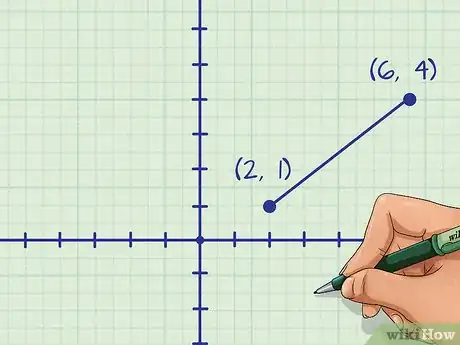
- Por ejemplo, un segmento de línea puede tener un extremo en las coordenadas y el otro en .
-
3Introduce las coordenadas en la fórmula de la distancia. Ten cuidado al sustituir los valores, asegúrate de que sean las variables correctas. Las dos coordenadas deben ir en el primer conjunto de paréntesis y las dos coordenadas deben ir dentro del segundo conjunto de paréntesis.
- Por ejemplo, para los puntos y , la fórmula queda así:
Anuncio
Parte 2
Parte 2 de 2:Calcular la distancia
-
1Calcula la resta entre paréntesis. Siguiendo el orden de las operaciones, cualquier cálculo que esté entre paréntesis deberá completarse primero.
- Por ejemplo:
- Por ejemplo:
-
2Eleva al cuadrado el valor entre paréntesis. El orden de las operaciones establece que los exponentes se deben calcular después.
- Por ejemplo:
- Por ejemplo:
-
3Añade los números que se encuentran debajo del signo de radical. Harás este cálculo como si estuvieras trabajando con números enteros.
- Por ejemplo:
- Por ejemplo:
-
4Obtén el valor de . Para conseguir la respuesta final, encuentra la raíz cuadrada de la suma debajo del signo de radical.
- Debido a que vas a encontrar la raíz cuadrada, es muy probable que necesites redondear tu respuesta.
- Ya que estás trabajando en un plano de coordenadas, tu respuesta estará en "unidades" genéricas, no en centímetros, metros ni otras unidades métricas.
- Por ejemplo:
unidades
Anuncio
Consejos
- No confundas esta fórmula con otras, como la fórmula del punto medio, la fórmula de la pendiente, la ecuación de una línea o la fórmula de la línea.
- Recuerda el orden de las operaciones al calcular tu respuesta. Resta primero, después saca el cuadrado de la diferencia, luego suma y por último encuentra la raíz cuadrada.




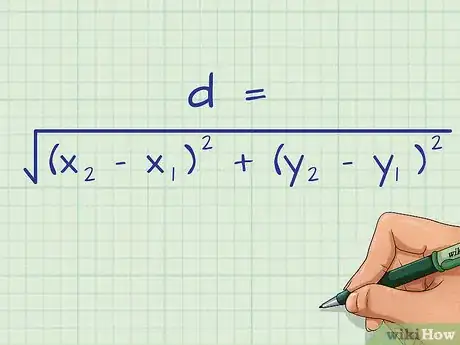







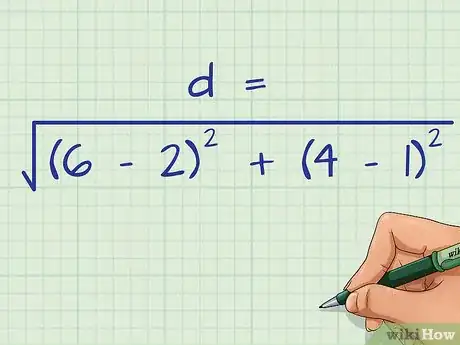



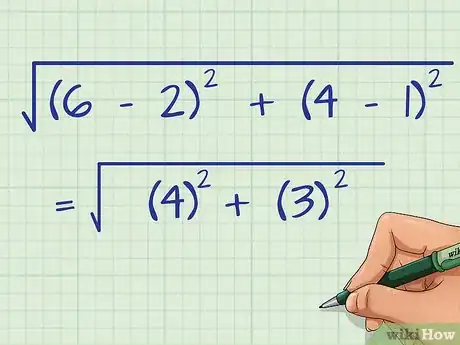

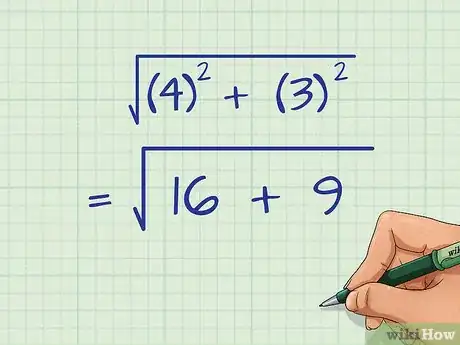

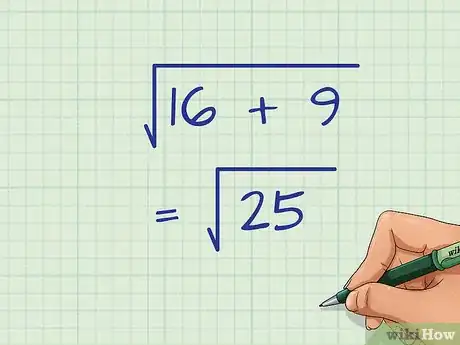

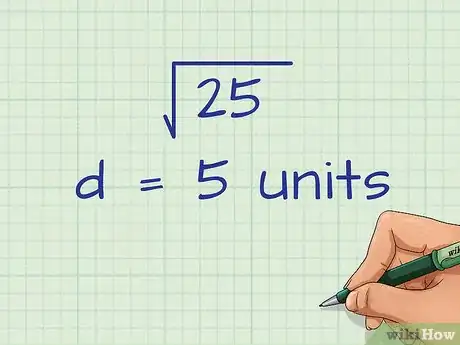




















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 31 238 veces.