Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 10 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 175 887 fois.
En géométrie, le périmètre d'un trapèze est la somme de la longueur de ses côtés. Lorsque toutes les informations sont disponibles, ce calcul est aisé [1] . Dans le cas contraire, le calcul du périmètre nécessite plusieurs étapes intermédiaires afin de trouver les dimensions manquantes. Le recours aux théorèmes mathématiques ou à la trigonométrie peut alors être nécessaire. Concernant les notations utilisées dans l'article, sachez que la longueur d'un segment [AB] s'écrit AB.
Étapes
Méthode 1
Méthode 1 sur 3:Calculer le périmètre d'un trapèze connaissant toutes ses dimensions
-
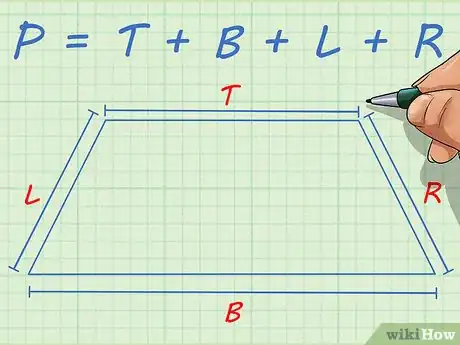
1Notez la formule de calcul du périmètre d'un trapèze ABCD. Soit [DC] la grande base, [AB] la petite base, [AD] et [BC] les deux autres côtés du polygone. Comme pour tous les quadrilatères, le périmètre P du trapèze est égal à la somme de la longueur des quatre côtés [2] . En l'espèce, il est donné par la formule suivante : P = AB + BC + CD + DA.
-
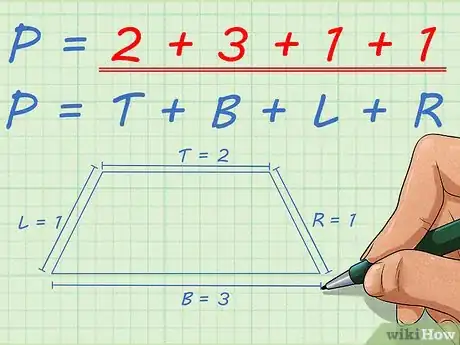
2Intégrez les valeurs numériques dans la formule. Pour calculer le périmètre d'un trapèze en une étape, vous devez disposer de ses quatre longueurs.
- Supposons les longueurs suivantes, exprimées en centimètres : DC = 3, AB = 2, AC = BC = 1. Dans ce cas particulier, notez qu'il s'agit d'un trapèze isocèle, car ses côtés non parallèles ont la même longueur.
-
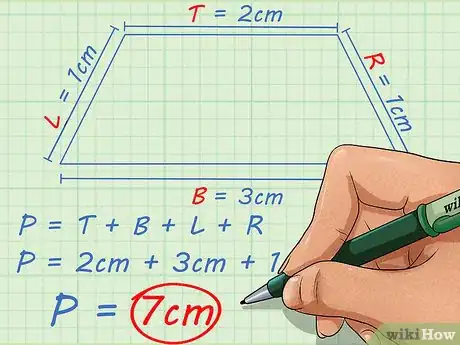
3Additionnez les longueurs. Si l'on reprend les valeurs numériques, le périmètre du trapèze est de 7 cm.
- Le calcul détaillé est P = 3 + 2 + 1 + 1 = 7.
Publicité
Méthode 2
Méthode 2 sur 3:Calculer le périmètre d'un trapèze à l'aide du théorème de Pythagore
-
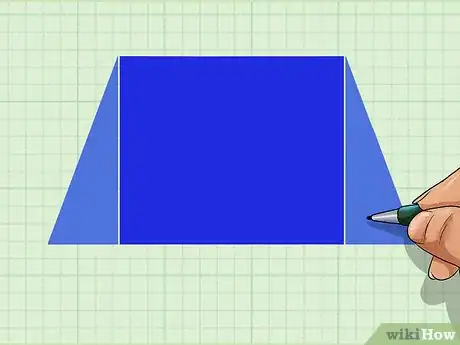
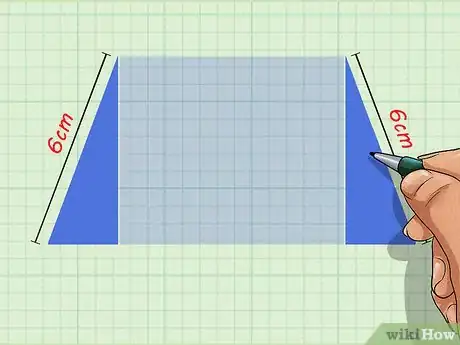
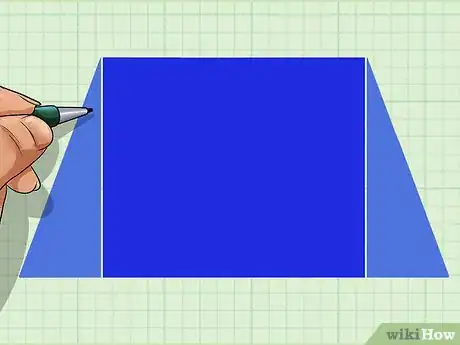
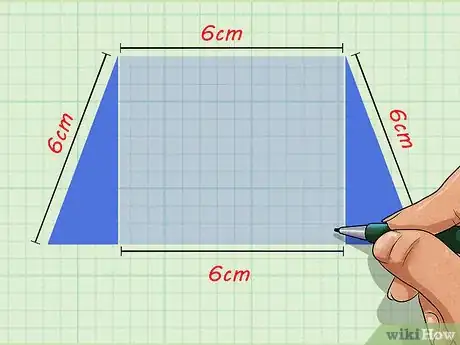
1Décomposez votre trapèze en trois figures plus simples. Soit ABCD un trapèze dont vous connaissez la hauteur, les dimensions de la petite base [AB] ainsi que des côtés non parallèles [AD] et [BC]. La longueur de la grande base [DC] est donc l'inconnue que vous devez trouver. Pour cela, il faut décomposer le polygone. Le trapèze est un quadrilatère particulier, car ses bases sont parallèles. Il est ainsi possible de le diviser en trois figures simples, à savoir un rectangle encadré par deux triangles rectangles. Pour les figurer, tracez les deux hauteurs issues des sommets A et B [3] .
- Pour calculer le périmètre d'un trapèze rectangle, divisez‑le en deux figures simples. En effet, il dispose d'au minimum un angle droit et peut être décomposé en un rectangle et un triangle rectangle [4] .
-
2Nommez les sommets de votre figure. Outre les points A, B, C et D du trapèze initial, ajoutez les points H1 et H2. Ils représentent les intersections entre les hauteurs et la grande base. Vous obtenez ainsi les triangles BCH2 et ADH1.
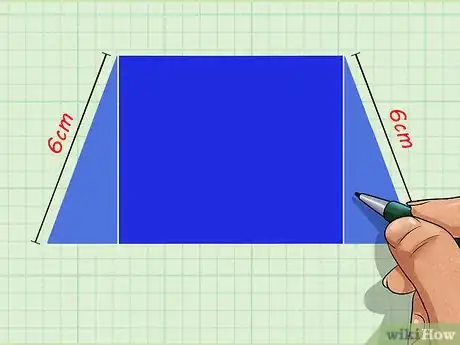
- Les bases du trapèze étant parallèles, les deux hauteurs ont la même longueur. Celle‑ci est également la largeur du rectangle. Supposons que la hauteur du trapèze mesure 6 cm. Vous avez donc AH1 = BH2 = 6.
-
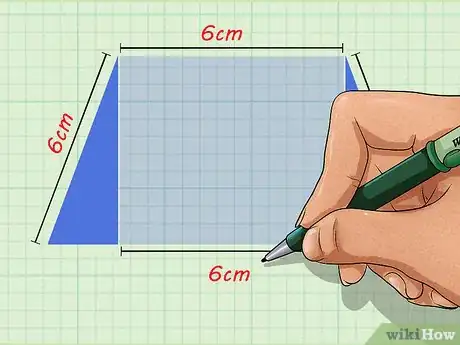
3Notez les dimensions du rectangle ABH2H1. Le découpage du trapèze permet de les déduire aisément. La longueur du rectangle est égale à celle de la petite base du trapèze et sa largeur équivaut à la hauteur.
- Supposons que la petite base mesure 6 cm. La longueur du rectangle est également de 6 cm, ce qui donne AB = H2H1 = 6. Dans ce cas particulier, notez que le polygone ABH2H1 est un carré. Ceci dit, cette observation n'impacte pas le calcul.
-
4Utilisez le théorème de Pythagore pour calculer les dimensions des triangles BCH2 et ADH1. Dans un triangle rectangle, l'hypoténuse est le côté opposé à l'angle droit, lequel est défini par une hauteur et la base associée [5] . Le théorème de Pythagore énonce que, dans le cas d'un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés [6] . Notez que, par abus de langage, la longueur du côté est assimilée audit côté.
-
5Appliquez le théorème de Pythagore au triangle BCH2. Soit [BC] son hypoténuse [BH2] sa hauteur et [CH2] sa base. Selon le théorème de Pythagore, le rapport des longueurs donne BC2 = BH22 + CH22.
- Notez que l'hypoténuse du triangle BCH2 est également le côté [BC] du trapèze. Vous disposez donc des longueurs de l'hypoténuse et d'un des côtés du triangle.
-
6Isolez la dimension inconnue du triangle. Pour cela, affinez la formule du théorème de Pythagore. Vous avez donc CH22 = BC2 - BH22. Donc CH2 = √(BC2 - BH22).
- Supposons BH2 = 6 et BC = 9. En insérant ces données dans la formule précédente, vous obtenez CH22 = (92 - 62) = 45.
-
7Calculez la longueur de la base du triangle BCH2. Reprenez la formule établie à l'étape précédente. En intégrant les données numériques, vous obtenez CH22 = 45 soit CH2 = √45. Il faut ensuite simplifier ce résultat.
- Hormis les carrés parfaits, la racine carrée d'un nombre est rarement un entier. Par exemple, la racine carrée de 45 vaut 6,71. Le résultat simplifié donne donc √45 = √(9 x 5) = √9 x √5 = 3√5.
-
8Calculez la longueur de la base du triangle ADH1. Soit [AH1] sa hauteur [AD] son hypoténuse et [DH1] sa base. Pour calculer la longueur de la base, appliquez à nouveau la formule du théorème de Pythagore. Pour le triangle ADH1, vous avez AD2 = AH12 + DH12. En isolant la base, vous obtenez DH12 = AD2 - AH12, ce qui donne DH1 = √(AD2 - AH12). Notez que, si vous cherchez le périmètre d'un trapèze isocèle, les côtés latéraux ont la même longueur. En décomposant cette figure, vous obtenez deux triangles identiques, ce qui facilite les calculs.
- Supposons AH1 = 6 et AD = 7. Cela donne DH1 = √(72 - 62) = √13.
-
9Calculez le périmètre de votre trapèze. Calculez la longueur de la grande base. Compte tenu des résultats précédents, vous avez DC = DH1 + H1H2 + H2C. La formule du périmètre P est donc P = DH1 + H1H2 + H2C + AB + BC + AD. Il est préférable de garder vos valeurs, notamment les racines carrées, sous forme d'entier.
- En remplaçant par les valeurs numériques, vous obtenez DC = √13 + 6 + 3√5 et P = √13 + 6 + 3√5 + 6 + 9 + 7 = 28 + 3√5 + √13. Le périmètre du trapèze est donc de 38,3 cm (arrondi au dixième près).
Publicité
Méthode 3
Méthode 3 sur 3:Calculer le périmètre d'un trapèze à l'aide de la trigonométrie
-
1Divisez le trapèze en trois figures simples. Soit un trapèze ABCD dont vous connaissez la hauteur, la dimension de la petite base [AB] et la valeur des angles définis par la grande base. Comme dans la méthode précédente, la décomposition du trapèze facilite le calcul. Tracez les hauteurs issues des sommets A et B de votre trapèze.
- Notez H1 et H2 les points d'intersection entre les hauteurs et la grande base. Votre trapèze est ainsi divisé en un rectangle ABH2H1 et deux triangles rectangles, notés BCH2 et ADH1.
-
2Déduisez la largeur du rectangle. Dans la mesure où les bases du trapèze sont parallèles, les deux hauteurs ont la même longueur. Elle est également la largeur du rectangle.
- Supposons que la hauteur mesure 6 cm. Vous avez donc AH1 = BH2 = 6.
-
3Déduisez la longueur du rectangle ABH2H1. Elle est égale à celle de la petite base [AB].
- Supposons que la petite base mesure 6 cm. Vous avez donc AB = H1H2 = 6. Dans ce cas particulier, la largeur et la longueur du rectangle sont identiques, ce qui en fait un carré.
-
4Calculez les dimensions des côtés non parallèles du trapèze. Compte tenu de vos données, vous pouvez les trouver grâce à la trigonométrie. En effet, les côtés non parallèles du trapèze se confondent avec l'hypoténuse des triangles rectangles qui le composent. Or, dans un triangle rectangle, le sinus d'un angle est égal au rapport entre les longueurs du côté opposé à l'angle et de l'hypoténuse [7] .
- Vous disposez de la valeur des angles en C et en D ainsi que de la hauteur du trapèze. Or, dans les triangles BCH2 et ADH1, les segments [BH2] et [AH1] sont respectivement les côtés opposés à ces angles. Vous pouvez donc calculer la longueur de leur hypoténuse grâce à la formule du sinus.
- La trigonométrie est un outil intéressant dans les calculs géométriques. Outre le sinus, vous pouvez également utiliser le cosinus [8] ou la tangente [9] d'un angle pour trouver une dimension dans un triangle rectangle.
-
5Calculez la longueur de l'hypoténuse du triangle BCH2. Soit [BC] l'hypoténuse du triangle α2 l'angle en C et [BH2] le côté opposé à cet angle. En reprenant la relation trigonométrique, vous avez sin α2 = BH2 / BC.
- Supposons que l'angle en C mesure 35°. Cela donne sin 35 = BH2 / BC.
-
6Calculez le sinus de l'angle en C. Il n'existe que quelques valeurs remarquables en trigonométrie. Pour les autres, vous devez utiliser une calculatrice scientifique.
- Dans notre exemple, le sinus de l'angle en C vaut 0,57. Vous pouvez conserver la valeur entière comportant le sinus ou l'arrondir. La précision de l'arrondi dépend de celle requise par votre travail.
-
7Calculez la valeur numérique de l'hypoténuse du triangle BCH2. En reprenant la formule trigonométrique précédente, vous obtenez BC = BH2 / sin α2.
- Avec les données numériques, vous obtenez BC = 6 / sin 35 = 10,46. Le côté [BC] du trapèze mesure donc 10,5 cm (arrondi au dixième près).
-
8Procédez de même pour le triangle ADH1. Le sinus de l'angle en D, noté α1, correspond au rapport entre les longueurs du côté opposé [AH1] et de l'hypoténuse [AD]. En reprenant la formule trigonométrique, vous obtenez donc sin α1 = AH1 / AD soit AD = AH1 / sin α1.
- Supposons que l'angle en D mesure 45°. Vous avez donc AD = 6 / sin 45 = 8,49. Le côté [AD] du trapèze mesure 8,5 cm (arrondi au dixième près).
-
9Calculez la longueur de la base des triangles. Cela vous permettra de déterminer la longueur de la grande base du trapèze. Grâce à vos précédents calculs, vous pouvez utiliser le théorème de Pythagore. Dans un triangle rectangle, le rapport des longueurs est particulier. Selon le théorème de Pythagore, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. Notez que, par abus de langage, la longueur d'un côté est désignée par ledit côté.
-
10Calculez la longueur de la base du triangle BCH2. Il s'agit du segment [CH2]. En reprenant la formule du théorème de Pythagore et les notations précédentes, BC2 = BH22 + CH22. En isolant la longueur de la base, vous obtenez CH2 = √(BC2 - BH22).
- Avec les données numériques, vous avez CH2 = √(10,52 - 62) = 8,56. Le segment [CH2] mesure 8,6 cm (arrondi au dixième près).
-
11Procédez de même pour le triangle ADH1. En appliquant la formule du théorème de Pythagore, vous avez AD2 = AH12 + DH12. En isolant la longueur de la base, vous obtenez DH1 = √(AD2 - AH12).
- En incluant les données numériques, la longueur de la base du triangle vaut 6 cm. Le calcul est DH1 = √(8,52 - 62) = 6,02. Le segment [DH1] mesure donc 6 cm (arrondi au dixième près).
-
12Calculez la longueur de la grande base. Elle est la somme de la longueur du rectangle et des bases des triangles que vous avez calculées. En reprenant les notations précédentes, vous avez DC = DH1 + H1H2 + CH2.
- En intégrant les données numériques, vous obtenez DC = 6 + 6 + 8,6 = 20,6. La grande base de trapèze mesure 20,6 cm.
-
13Calculez le périmètre du trapèze. Sommez les dimensions des côtés du polygone. La formule du périmètre P est la suivante : P = AB + BC + CD + DA.
- En remplaçant par les valeurs numériques, vous obtenez P = 6 + 10,5 + 20,6 + 8,5 = 45,6. Le périmètre du trapèze est donc de 45,6 cm.
Publicité
Conseils
- Utilisez les propriétés des triangles particuliers afin de trouver les dimensions manquantes. Par exemple, sachez que les rapports entre les longueurs sont remarquables dans le cas des triangles rectangles isocèles ou des triangles rectangles possédant des angles de 30° et 60° [10] .
- Gardez une calculatrice scientifique à portée de main. Elle est indispensable pour les calculs trigonométriques et la conversion des racines carrées. Vous pouvez également en trouver en ligne.
- Indiquez les dimensions directement sur votre figure au fur et à mesure.
- À moins que vos calculs nécessitent une précision absolue, vous pouvez vous contenter d'arrondir les dimensions au dixième près.
Éléments nécessaires
- Une calculatrice scientifique
- Un crayon à papier
- Une feuille de papier
Références
- ↑ http://www.recreomath.qc.ca/am_trapeze.htm
- ↑ http://maths.samomoi.com/trapeze-508.php
- ↑ https://www.geogebra.org/m/TJB7GM2K
- ↑ http://warmaths.fr/MATH/geometr/quadrlla/trapeze.htm
- ↑ http://www.comment-calculer.net/aire-du-triangle-rectangle.php
- ↑ http://myriam.collenne.free.fr/4_pythagore.htm
- ↑ http://www.trigofacile.com/maths/trigo/notions/fonctions/rectangle.htm
- ↑ http://maths.vivien.free.fr/Documents/4e/CR4_cosinus.pdf
- ↑ http://www.bibmath.net/dico/index.php?action=affiche&quoi=./t/tangentef.html
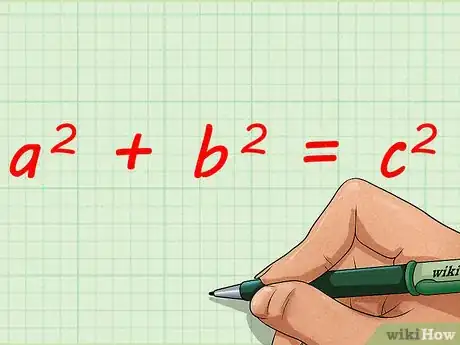
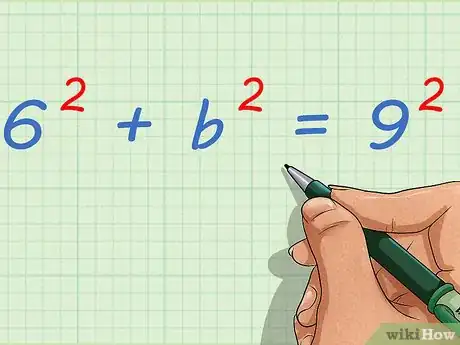
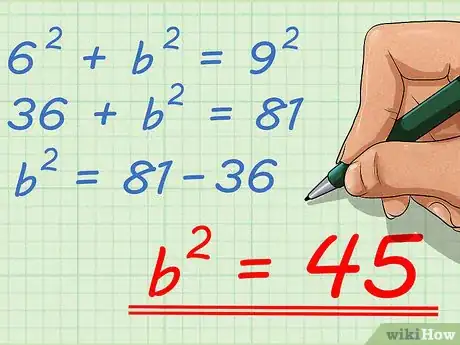
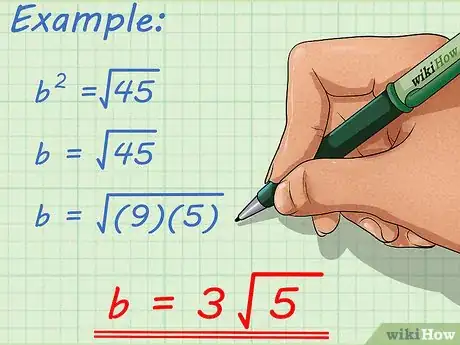




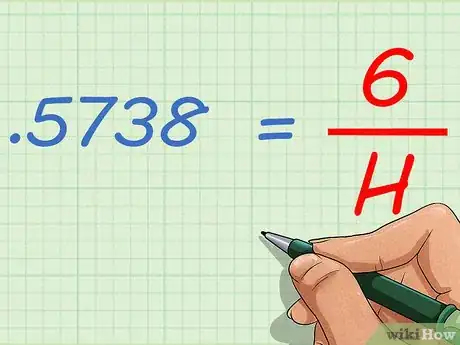


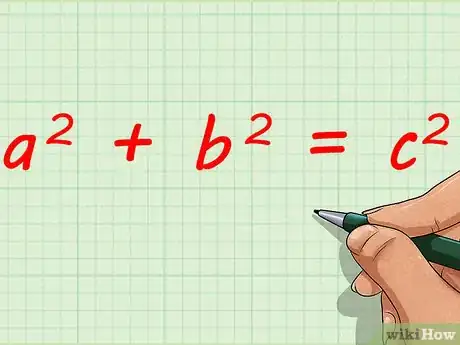


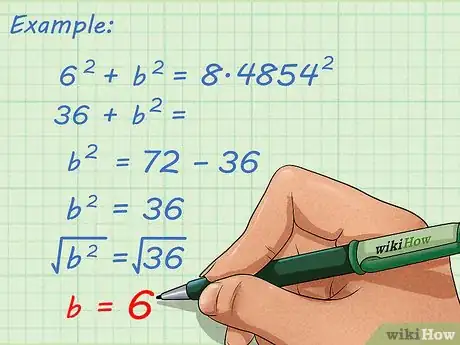

















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 175 887 fois.