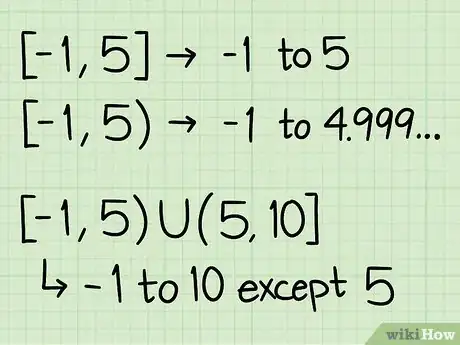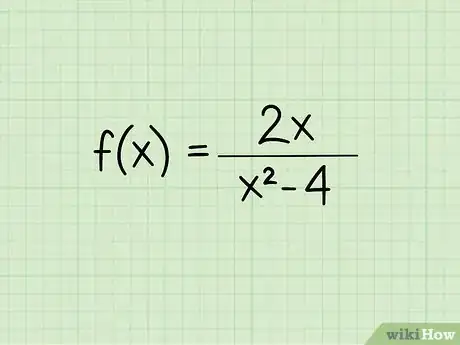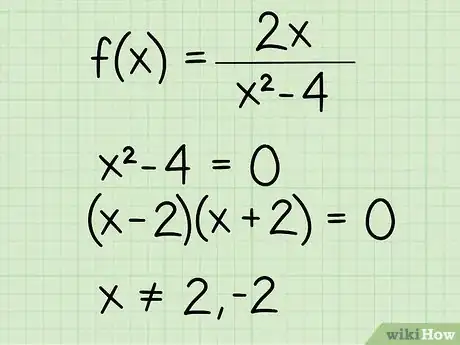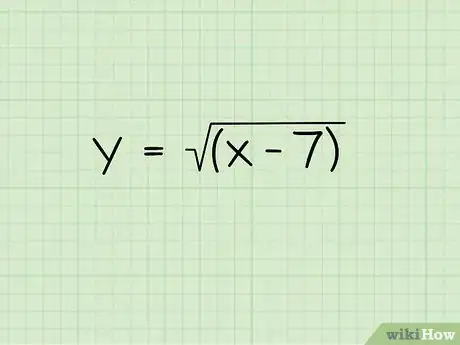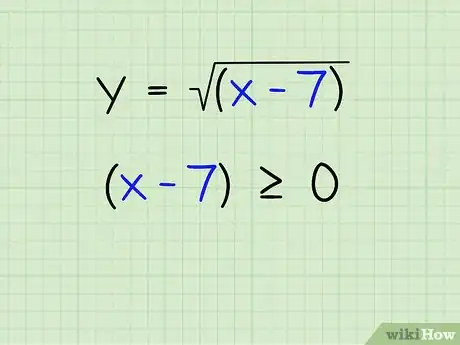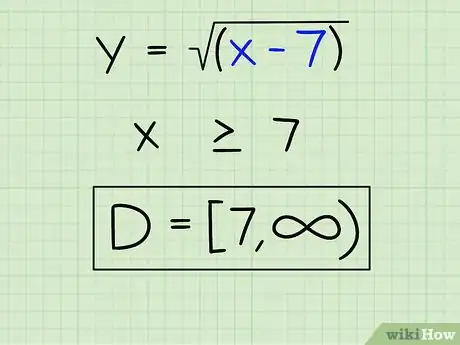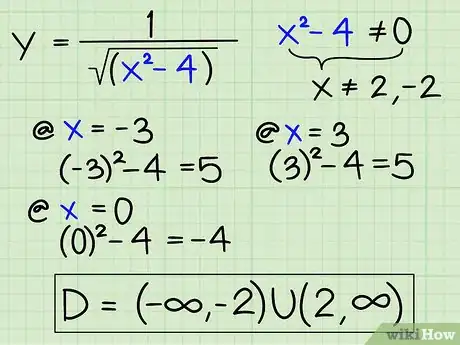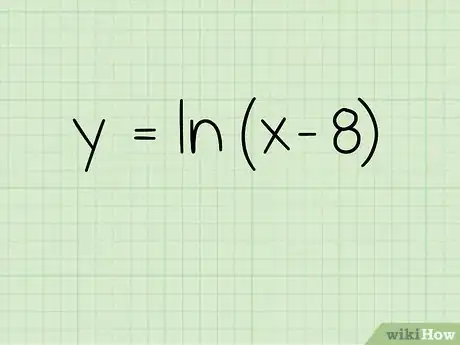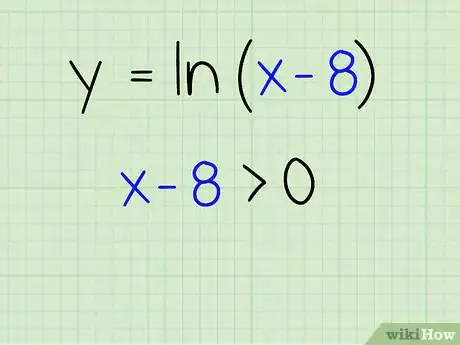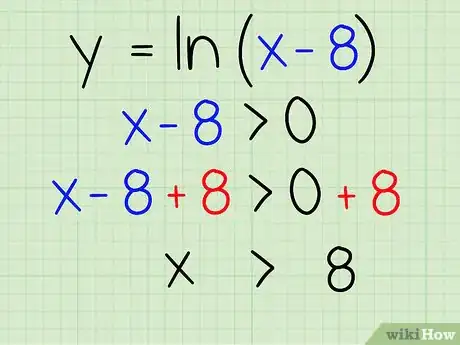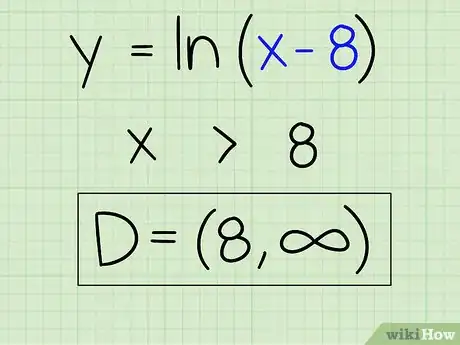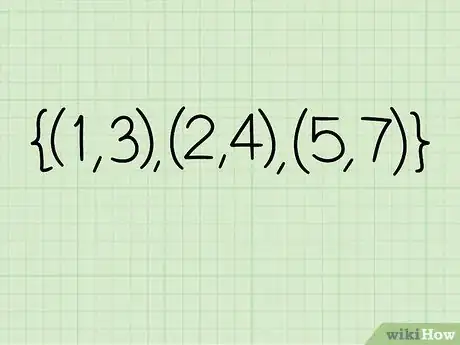wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 16 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 531 777 fois.
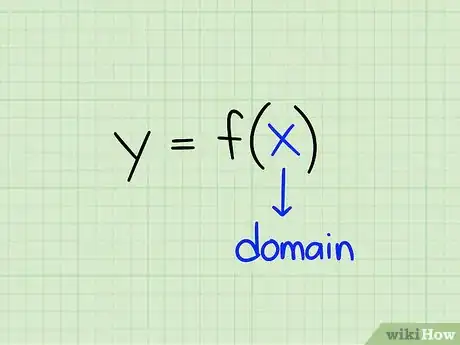
Le domaine (ou ensemble) de définition d'une fonction, f(x) par exemple, est l'ensemble des valeurs de x pour lesquels f(x) existe. En clair, ce sont toutes les valeurs de x qui permettent d'obtenir un résultat dans f(x). Les valeurs y qui en résultent forment l'ensemble des images de x. Si on vous demande régulièrement de trouver le domaine de définition de telle ou telle fonction, il suffit d’appliquer une méthode de résolution appropriée qui dépend de la nature du problème posé.
Étapes
Méthode 1
Méthode 1 sur 6:Tenir compte de quelques éléments de base
-
1Comprenez la signification du domaine de définition ! Ce dernier se définit comme l'ensemble des valeurs de x pour lesquels f(x) existe. Autrement dit, si vous prenez une valeur pour x, que vous la mettez dans l'équation et que vous trouvez un résultat, alors x fait partie du domaine de définition. C'est l'ensemble de tous ces x qui constitue le domaine de définition.
-
2Sachez que le domaine de définition varie. Il dépend de la fonction que vous avez à traiter. Vous trouverez ci-dessous les principes généraux pour déterminer le domaine de définition de tel ou tel type de fonction. Ces principes seront détaillés et illustrés un peu plus loin.
- Pour une fonction polynôme, sans racine ni inconnue en position de dénominateur, le domaine de définition est l'ensemble des réels, soit l'ensemble R.
- Pour une fonction avec une inconnue en dénominateur, le domaine de définition est l'ensemble des réels, soit l'ensemble R moins la valeur de x qui annule le dénominateur (si x-2 est en dénominateur, le domaine est R moins la valeur 2).
- Pour une fonction avec une inconnue dans une racine, le domaine de définition est l'ensemble des réels, R, moins l'ensemble des valeurs de x qui donnent un radicande (expression mathématique sous le symbole de la racine) négatif.
- Pour une fonction avec un logarithme type « ln », la valeur dont on prend le logarithme doit être strictement supérieure à 0.
- Pour une fonction à partir de sa courbe, on lit directement sur l'axe des abscisses les valeurs entre lesquelles la courbe s'inscrit.
- Pour un graphe, qui est une liste de points avec les coordonnées x et y, le domaine de définition est tout simplement l'ensemble des abscisses des points, soit les valeurs de x.
-
3Écrivez correctement le domaine de définition. Présenter un domaine de définition est finalement assez simple, mais il faut suivre une norme précise pour présenter la bonne réponse et avoir ainsi tous vos points lors d'un examen. Voici les principes normatifs à connaitre pour bien présenter le domaine de définition d'une fonction.
- Un domaine de définition se présente sous la forme suivante : un crochet ou une parenthèse d'ouverture, suivi(e) par deux bornes (ou valeurs) séparées par une virgule et enfin un crochet ou une parenthèse de fermeture.
- Par exemple, si on écrit [-1,5), cela signifie que le domaine de définition inclut toutes les valeurs de -1 (compris) à 5 (non compris).
-
Les crochets - [ et ] - indiquent qu'on prend la ou les valeurs qui sont avant ou après lesdits crochets.
- Dans l'exemple précédent, [-1,5), -1 est compris dans le domaine de définition.
-
À l'inverse, les parenthèses - ( et ) - indiquent qu'on ne prend pas la ou les valeurs qui sont avant ou après lesdites parenthèses.
- Dans l'exemple précédent, [-1,5), 5 n'est pas compris dans le domaine de définition. Ce dernier s'arrête donc à 4 999.
-
On utilise aussi le symbole « U » (comme « union ») au cas où le domaine de définition se compose deux ou plusieurs intervalles.
- Par exemple, si le domaine de votre fonction est [-1,5) U (5,10], cela veut dire que les valeurs de x qu'on peut utiliser se trouvent dans l'intervalle de -1 à 10, mais que la valeur 5 ne s'y trouve pas. Ce pourrait être une fonction dans laquelle on ait une fraction où « x - 5 » serait en position de dénominateur.
- Le nombre de symboles « U » est illimité. Il arrive que des fonctions un peu complexes aient des domaines composés de plusieurs intervalles.
-
On peut utiliser les symboles « moins l'infini » (- ∞) ou « plus l'infini » (+ ∞) pour indiquer que les valeurs de x sont illimitées d'un côté ou d'un autre ou des deux à la fois.
- Avec les symboles infinis, on ne met que des parenthèses - ( ) -, pas des crochets - [ ].
Publicité - Un domaine de définition se présente sous la forme suivante : un crochet ou une parenthèse d'ouverture, suivi(e) par deux bornes (ou valeurs) séparées par une virgule et enfin un crochet ou une parenthèse de fermeture.
Méthode 2
Méthode 2 sur 6:Chercher le domaine de définition d'une fonction avec une fraction
-
1Inscrivez l'équation de votre fonction. Prenons l'équation suivante :
- f(x) = 2x/(x2 - 4)
-
2Examinez l’inconnue. Elle est sous la barre de fraction et comme on ne peut pas diviser un nombre par 0, il faut donc éliminer la valeur de x qui donne un dénominateur égal à 0. Vous devez donc poser l'équation suivante : dénominateur ≠ 0 et la résoudre. Dans notre cas, cela donne :
- f(x) = 2x/(x2 - 4)
- x2 - 4 ≠ 0
- (x - 2)(x + 2) ≠ 0
- x ≠ 2 et x ≠ - 2
-
3Établissez le domaine de définition. On obtient :
- x peut prendre toutes les valeurs sauf 2 et -2
Publicité
Méthode 3
Méthode 3 sur 6:Chercher le domaine de définition d'une fonction avec une racine carrée
-
1Inscrivez l'équation de votre fonction. Prenons l'équation suivante : y =√(x-7).
-
2Analysez le radicande. Celui-ci doit être forcément positif ou nul. En effet, on ne peut pas extraire la racine carrée d'un nombre négatif. Par contre, on peut le faire avec 0. Donc, il vous faut poser l'inéquation suivante : radicande ≧ 0. Ceci n'est valable que pour les racines carrées (2) ou les racines à puissance paire (4, 6…). Pour les racines cubiques (3) ou de puissance impaire (5, 7…), cette condition n'est pas nécessaire. Pour notre cas, cela donne :
- x-7 ≧ 0
-
3Isolez l'inconnue. Il vous faut isoler l'inconnue à gauche en ajoutant 7 aux deux membres de l'inéquation, ce qui donne :
- x ≧ 7
-
4Établissez maintenant le domaine de définition (D). La réponse est :
- D = [7, ∞)
-
5Trouvez le domaine de définition d'une fonction avec une racine carrée. Elle doit accepter deux réponses. Soit la fonction : y = 1/√(x2 -4). On cherche les solutions de « l'équation-radicande », x2 -4 = 0. Il y en a deux : 2 et - 2. Maintenant on se retrouve avec trois intervalles : de - ∞ à -2, de -2 à 2 et de 2 à + ∞. Voici comment on fait pour savoir ceux qui composent le domaine de définition.
- On prend un x qui est dans le premier intervalle (- 3 par exemple) et on le met dans l'équation. On obtient :
- (-3)2 - 4 = 9 - 4 = 5. Le radicande est positif, c'est bon, on prend cet intervalle !
- On prend un x qui est dans le deuxième intervalle (-0 par exemple) et on le met dans l'équation. On obtient :
- 02 - 4 = 0 -4 = - 4. Le radicande est négatif, ça ne marche pas, on ne prend pas cet intervalle !
- On prend un x qui est dans le troisième intervalle (3 par exemple) et on le met dans l'équation. On obtient :
- 32 - 4 = 9 - 4 =5. Le radicande est positif, c'est bon, on prend cet intervalle !
- Inscrivez le domaine de définition définitif (D). On obtient ainsi :
- D = (-∞, -2) U (2, + ∞)
Publicité - On prend un x qui est dans le premier intervalle (- 3 par exemple) et on le met dans l'équation. On obtient :
Méthode 4
Méthode 4 sur 6:Chercher le domaine de définition d'une fonction avec un logarithme
-
1Inscrivez l'équation de votre fonction. Prenons l'équation suivante :
- f(x) = ln(x-8)
-
2Examinez l’expression entre parenthèses. Elle doit être strictement positive. On ne peut calculer le log que d'une valeur strictement positive, c'est pour cela qu'on va le vérifier ici, avec notre équation :
- x - 8 > 0
-
3Résolvez l'inéquation. Isolez l'inconnue d'un côté en ajoutant 8 des deux côtés :
- x - 8 + 8 > 0 + 8
- x > 8
-
4Inscrivez le domaine de définition définitif (D). Il se compose de toutes les valeurs qui vont de 8 (non compris) à + ∞ :
- D = (8,∞)
Publicité
Méthode 5
Méthode 5 sur 6:Chercher le domaine de définition d'une fonction à partir de sa courbe
-
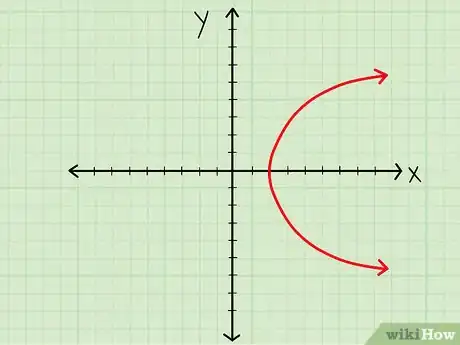
1Regardez attentivement la courbe de la fonction.
-
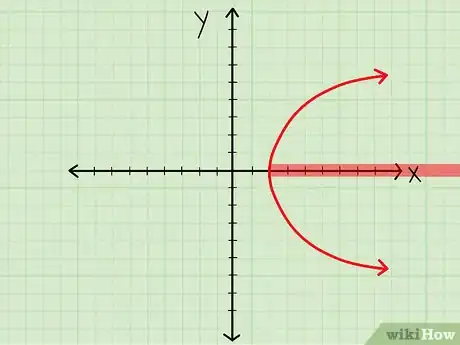
2Repérez les valeurs de x à l'intérieur desquelles s'inscrit la courbe. « Plus facile à dire qu'à faire », me direz-vous ! Voici quelques conseils pour vous aider.
- Si votre courbe est une droite, elle est sans fin, d'un côté comme de l'autre. Son domaine de définition regroupe n'importe quelle valeur de x, c'est donc l'ensemble des réels.
- Si votre courbe est une parabole « verticale », c'est-à-dire qu'elle s'ouvre soit vers le haut soit vers le bas, alors le domaine de définition sera l'ensemble des réels. Prenez n'importe quel x, vous trouverez toujours une valeur « y » qui y est associée.
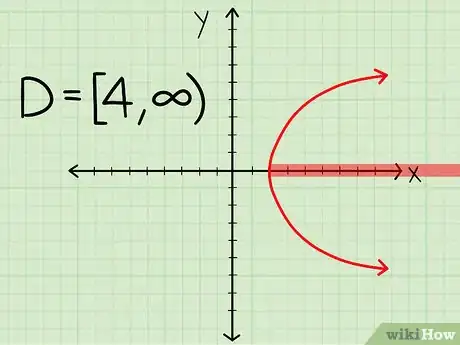
- Si votre courbe est une parabole « horizontale », avec un sommet au point (4,0), elle s'ouvre donc vers la droite. Elle n'ira jamais à gauche de ce point. Le domaine de définition, D, sera [4, ∞).
-
3Inscrivez le domaine de définition définitif en fonction de la courbe. Si vous avez un doute sur les limites du domaine de définition, testez, dans l'équation de la fonction, avec quelques valeurs de x, vous allez vite voir si vous avez juste ou si vous vous êtes trompé(e) !Publicité
Méthode 6
Méthode 6 sur 6:Chercher le domaine de définition d'un graphe
-
1Notez les éléments du graphe. C'est un ensemble de points avec leurs coordonnées x et y. Prenons par exemple : {(1, 3), (2, 4), (5, 7)}.
-
2Récupérez les abscisses (les « x »). Ici, c'est : 1, 2, 5.
-
3Le domaine de définition sera D = {1, 2, 5}.
-
4Assurez-vous que votre graphe est bien celui d'une fonction. Pour ce faire, il faut qu'à chaque « x » corresponde toujours le même « y ». Ainsi, si x = 3, « y » devra être toujours égal à 6, etc. On dit aussi que « x » ne doit pas posséder plus d'une image. Le graphe suivant, {(1, 4), (3, 5), (1, 5)}, n'est pas une fonction parce qu'avec un même « x », on obtient deux valeurs de « y » différentes[1] .Publicité