wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 14 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 78 699 fois.
L'ensemble des images d'une fonction regroupe toutes les valeurs « y » d'une fonction - f(x) - donnée. Chaque fois que vous donnez une nouvelle valeur à « x », vous obtenez une valeur « y » qu'on appelle une image. Toutes les valeurs « x » qui donnent une image dans la fonction forment ensemble le domaine de définition de la fonction. Ici, on va faire le travail opposé, vous aider à déterminer l'ensemble des images d'une fonction. Lisez plutôt !
Étapes
Méthode 1
Méthode 1 sur 4:Trouver l'ensemble des images d'une fonction à partir de son équation
-
1Écrivez l'équation de la fonction. Prenons la fonction suivante : f(x) = 3x2 + 6x -2 qu'on peut aussi écrire y = 3x2 + 6x -2. Chaque fois que vous donnerez une valeur à x, vous obtiendrez une valeur y. La courbe associée à cette équation est une parabole.
-
2Trouvez le sommet de la courbe dans le cas d'une équation du second degré. Si vous avez une fonction linéaire (type f(x) = 2x+2) ou une fonction du troisième degré ou d'un degré impair (type f(x) = 6x3+2x + 7), vous pouvez passer cette étape. Par contre, si vous avez une équation de droite dans laquelle « x » est élevé au carré (ou à une puissance paire), vous devez déterminer le sommet de la courbe. Pour ce faire, on calcule d'abord l'abscisse de ce point avec la formule : -b/2a. Dans notre fonction de type ax2 + bx -c, soit 3x2 + 6x -2, on a 3 = a, 6 = b et -2 = c. On calcule : -b/2a = -6/2 x 3 = -6/6, soit au final -1, l'abscisse du sommet[1] .
- Il ne reste plus qu'à trouver l'ordonnée (y) de ce même point. On remplace x par -1, ce qui donne : f(-1) = 3(-1)2 + 6(-1) -2 = 3 - 6 -2 = -5.
- Le sommet a pour coordonnées (-1, -5). Placez ce point sur votre courbe au croisement de -1 et de 5. Ce point est dans le troisième quadrant du repère (en bas à gauche).
-
3Trouvez quelques autres points pour tracer la courbe. Afin de pouvoir tracer votre parabole, qui est symétrique, calculez quelques autres points. Le coefficient de x2 est positif, donc la parabole s'ouvre vers le haut. Pour tracer correctement une parabole, il faut calculer quelques points :
- f(-2) = 3(-2)2 + 6(-2) -2 = -2. Le point (-2, -2) est constitutif de la parabole
- f(0) = 3(0)2 + 6(0) -2 = -2. Le point (0, -2) est aussi constitutif de la parabole
- f(1) = 3(1)2 + 6(1) -2 = 7. Quant au point (1, 7), il est également sur la courbe.
-
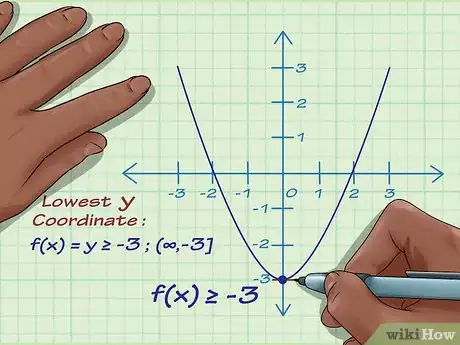
4Vous pouvez maintenant lire l'ensemble des images sur la courbe. Intéressez-vous à l'axe des y (ordonnées), trouvez la valeur de y en dessous de laquelle la courbe ne descendra pas. Ici, elle n'ira pas plus bas que le sommet dont l'ordonnée est -5. Par contre, la courbe va vers « plus l'infini » dans l'autre sens. En conclusion, l'ensemble des images de cette fonction regroupe tous les nombres réels ≥ -5.Publicité
Méthode 2
Méthode 2 sur 4:Déterminer l'ensemble des images d'une fonction à partir de sa courbe
-
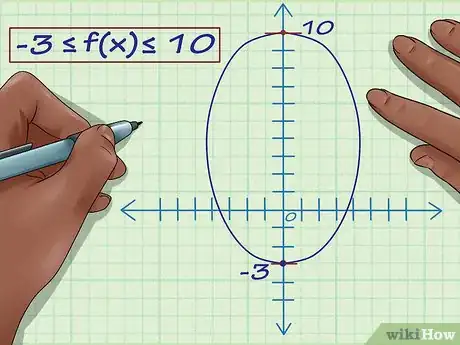
1Déterminez le minimum de la fonction. Repérez la plus petite ordonnée (axe des y) possible. Pour illustrer notre propos, nous dirons que ce minimum est à y =-3. Ce minimum peut être inférieur et même être à « moins l'infini ».
-
2Déterminez le maximum de la fonction. Pour illustrer notre propos, nous dirons que ce minimum est à y =10. Ce maximum peut être plus grand ou même être à « plus l'infini ».
-
3Établissez l'ensemble des images. Dans notre cas, « y » ne peut prendre qu'une valeur comprise entre -3 et 10 ou -3 ≤ f(x) ≤ 10 : c'est ça l'ensemble des images !
- Si on garde le même minimum (-3) et que le maximum est à « plus l'infini », alors l'ensemble des images sera : f(x) ≥ -3.
- Si on garde le même maximum (10) et que le minimum est à « moins l'infini », alors l'ensemble des images sera f(x) ≤ 10.
Publicité
Méthode 3
Méthode 3 sur 4:Déterminer l'ensemble des images d'un graphe
-
1Écrivez le graphe sur le papier. Un graphe est un ensemble de paires ordonnées (ou couples) avec des abscisses (x) et des ordonnées (y). On peut déterminer le domaine de définition et l'ensemble des images d'un graphe. Soit le graphe suivant : {(2, –3), (4, 6), (3, –1), (6, 6), (1, 3)}[2] .
-
2Faites la liste des ordonnées (y) du graphe. Cette tâche simple vous donne directement l'ensemble des images du graphe : {-3, 6, -1, 6, 3}[3] .
-
3Supprimez les valeurs en double pour n'en garder qu'une. Vous aurez remarqué qu'il y avait deux « 6 ». Supprimez-en un, ce qui nous donne : {-3, -1, 6, 3}[4] .
-
4Classez les images par ordre croissant. À ce stade, il faut classer les images de la plus petite à la plus grande. Ainsi, l'ensemble des images du graphe {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} est au final : {-3, -1, 3, 6}. Problème résolu[5] !
-
5Derrière un graphe, il doit toujours y avoir une fonction. Quelques explications : chaque fois que vous prenez un x, vous obtenez un y. Pour qu'il y ait graphe, on ne peut pas avoir deux valeurs pour un même x. Par exemple, le graphe {(2, 3) (2, 4) (6, 9)} n'en est pas un, puisque avec x=2, vous avez une fois, y=3 et une fois, y= 4. À un x donné, il ne peut y avoir qu'un seul y, même si x est négatif[6] .Publicité
Méthode 4
Méthode 4 sur 4:Trouver l'ensemble des images dans un exercice concret
-
1Lisez bien l'énoncé du problème. Soit l'exercice suivant : »Becky vend des billets pour son spectacle de fin d'année 5 euros pièce. La somme qu'elle récoltera à la fin est fonction du nombre de billets qu'elle aura vendus. Quel est l'ensemble des images de cette fonction ?«
-
2Reformulez le problème sous la forme d'une équation de fonction. Ici, « M » représentera le montant total perçu et « t » sera le nombre de tickets vendus. Le ticket coûtant 5 euros, il faut multiplier « t » par 5. L'équation de votre fonction s'écrit alors ainsi : M(t) = 5t.
- Si Becky vend 2 tickets, elle percevra 10 euros (2 x 5).
-
3Déterminez le domaine de définition de cette fonction particulière. Avant de trouver l'ensemble des images, il faut connaître l'ensemble de définition de la fonction. Le dernier conditionne le premier. Ici, Becky ne peut pas vendre moins de 0 tickets. Donc « t » n'est pas négatif, mais il peut être nul. Voilà pour la limite inférieure du domaine de définition. Pour l'autre limite, la supérieure, nous ne connaissons pas la taille de la salle de spectacle en question. Théoriquement, Becky peut vendre tous les billets. Au maximum, la borne supérieure sera le nombre de places de la salle. Par contre, elle ne peut pas vendre demi-billets ! Donc le domaine de définition (valeurs possibles de « t ») de notre fonction comprend tous les entiers positifs, y compris 0.
-
4Déterminez l'ensemble des images de cette fonction. Il regroupe tous les montants que Becky est susceptible de tirer de la vente de ses billets. Vous voyez ainsi que l'ensemble des images est corrélé au domaine de définition. On sait que « t » est un entier positif ou nul et que l'équation est M(t) = 5t. Si Becky vend 5 tickets, il gagnera 25 euros (5 x 5 euros) ; si elle en vend 100, elle en touchera 500 (100 x 5 euros). Donc, l'ensemble des images est ici tout entier positif ou nul, multiple de 5
- En d'autres termes, tout entier positif divisible par 5 est une image de notre fonction. 225 est une image, 365 aussi !
Publicité
Conseils
- Quelques mots sur la fonction inverse (qui s'écrit f-1(x)) : le domaine de définition de la fonction inverse d'une fonction est l'ensemble des images de la fonction de départ. À méditer !
- Voyez si votre fonction est bornée et périodique. Toute fonction bornée, quelle que soit la valeur de x, renvoie toujours une image comprise entre les deux mêmes valeurs. Ainsi, la fonction, f(x) = sin(x) a pour ensemble des images l'intervalle [-1,1]. Jamais la courbe ne dépassera ces deux valeurs de y !
Références
- ↑ http://www.uiowa.edu/~examserv/mathmatters/tutorial_quiz/geometry/findingvertexofparabola.html
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.mathsisfun.com/sets/domain-range-codomain.html