Comment calculer l'inverse d'une matrice 3x3

Il est fréquent en algèbre d'utiliser les inverses pour se faciliter la tâche. Pour diviser une valeur par une fraction, il est plus commode de multiplier cette valeur par l'inverse de cette fraction : c'est ce qu'on appelle une opération inverse. En ce qui concerne les matrices, la division n'a aucun sens : il faut alors en passer par la multiplication de la matrice inverse, ce qui suppose de la déterminer au préalable. Le calcul à la main de l'inverse d'une matrice 3x3 est un travail simple, mais un peu fastidieux, c'est cependant une opération très instructive au regard du fonctionnement des matrices. Si vous faites du calcul matriciel à longueur de journée, mieux vaut savoir utiliser une calculette graphique.

Méthode 1
Méthode 1 sur 3:
Établir une matrice adjointe pour trouver une matrice inverse

  1. Image intitulée Find the Inverse of a 3x3 Matrix Step 1
    1
    Trouvez le déterminant de la matrice. C'est la première chose à faire, car si le déterminant est nul (= 0), vous n'aurez pas besoin d'aller plus loin, la matrice n'aura pas d'inverse. On appelle conventionnellement det(A) le déterminant de la matrice A [1] .
    • Pour une matrice 3x3, commencez toujours par calculer son déterminant
    • Si vous voulez en savoir plus ou vous rafraichir la mémoire sur les déterminants, lisez cet article.
  2. Image intitulée Find the Inverse of a 3x3 Matrix Step 2
    2
    Transposez la matrice de départ. La transposition est une opération qui consiste en une symétrie par rapport à une diagonale, le but étant de permuter l'élément (i,j) et l'élément (j,i). Quand vous transposez une matrice le long d'une diagonale (généralement, celle qui va de la gauche en haut au bas à droite), les éléments sur cette diagonale demeurent inchangés [2] .
    • Il est une autre façon de penser la transposition, c'est de se dire que la première rangée devient la première colonne, que la ligne du milieu devient la colonne du milieu, et enfin, que la troisième ligne devient la troisième colonne. Observez l'image ci-dessus et voyez, à l'aide des couleurs, comment s'opère le changement de place.
  3. Image intitulée Find the Inverse of a 3x3 Matrix Step 3
    3
    Calculez les déterminants des neuf matrices mineures. Chaque élément de la matrice 3x3 transposée est associé à une matrice mineure. Pour trouver cette dernière, et il y en a neuf dans une matrice 3x3, il faut, par la pensée, éliminer tous les termes qui se trouvent sur la rangée et la colonne de l'élément considéré, soit cinq termes. Les quatre termes restants forment la matrice mineure associée à l'élément [3] .
    • Reprenons notre exemple et cherchons la matrice mineure associée au terme (a21) de la seconde rangée et de la première colonne. Encerclez les cinq termes de cette rangée et de cette colonne, les quatre restants sont ceux de la matrice mineure associée.
    • Calculez le déterminant (appelé aussi « mineur ») de chacune des matrices mineures en faisant les produits en croix et en soustrayant dans le bon sens.
    • Avec une matrice ayant a b sur la première rangée et c d sur la seconde, le déterminant est égal à : ad - bc.
  4. Image intitulée Find the Inverse of a 3x3 Matrix Step 4
    4
    Établissez la matrice des cofacteurs. Placez tous les déterminants que vous venez de calculer dans une matrice que nous allons appeler « matrice des cofacteurs ». Bien entendu, le déterminant sera placé à l'endroit du terme associé. Ainsi, le déterminant de la matrice mineure de l'élément (1,1) remplacera l'élément (1,1). Il ne reste plus qu'à changer éventuellement les signes. Le cofacteur Cij issu du déterminant Mij est déterminé par la relation : Cij = ((-1)i+j)(Mij) [4] .
    • Au moment d'attribuer les signes, le premier élément de la première rangée garde son signe, le second prend le signe opposé, le troisième garde son signe. Passez à la ligne suivante en respectant toujours l'alternance. L'illustration représente très bien ces multiplications qu'il faut faire pour trouver les cofacteurs. Les « + » et les « - » doivent être compris comme « +1 » et « -1 ».
    • Vous trouverez sur Internet de nombreux sites qui vous expliqueront en détail ce calcul des cofacteurs.
    • La matrice que vous venez d'obtenir est la matrice adjointe de la matrice de départ. On l'appelle aussi « comatrice » ou « matrice transconjuguée ». Elle est le plus souvent notée com(M) ou M*.
  5. Image intitulée Find the Inverse of a 3x3 Matrix Step 5
    5
    Divisez chaque terme de la matrice adjointe par le déterminant. Récupérez le déterminant de M qui a été calculé dans la première étape. Chaque résultat sera inscrit dans une nouvelle matrice en respectant les places. Ce que vous obtenez au terme de ces calculs est la matrice inverse de la matrice de départ [5] .
    • Si vous reprenez l'exemple, vous avez trouvé un déterminant égal à 1. Il faut donc diviser chaque élément de com(M) par cette valeur, ce qui la laisse inchangée. Ce ne sera pas toujours aussi rapide !
    • Dans certains ouvrages, on préfère multiplier com(M) par l'inverse du déterminant. En fait diviser par det(M) revient à multiplier par 1/det(M) : c'est exactement la même chose.
    Publicité

Méthode 2
Méthode 2 sur 3:
Utiliser la réduction linéaire par rangées pour trouver une matrice inverse

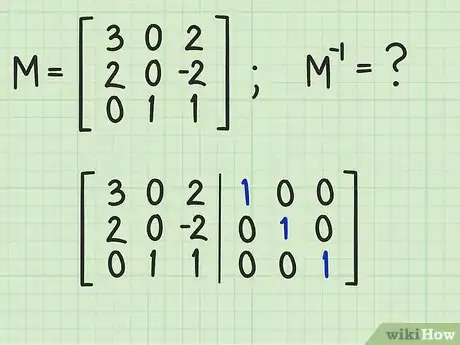
  1. Image intitulée Find the Inverse of a 3x3 Matrix Step 6
    1
    Accolez la matrice identité à votre matrice. Inscrivez sur votre feuille la matrice de départ M sans l'accolade de droite, tirez un trait vertical à droite de celle-ci, inscrivez la matrice identité et fermez l'accolade. Vous obtenez alors une sorte de matrice à trois rangées et six colonnes (matrice augmentée) [6] .
    • Rappelons ici que la matrice identité est une matrice un peu particulière dans laquelle la diagonale (qui part du haut à gauche et finit en bas à droite) est constituée de 1, les autres valeurs étant des 0. Nombreux sont les sites à proposer des pages sur cette matrice et ses propriétés.
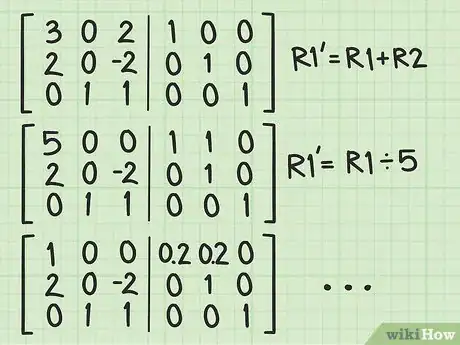
  2. Image intitulée Find the Inverse of a 3x3 Matrix Step 7
    2
    Appliquez l'algorithme de Gauss-Jordan. C'est une méthode de réduction linéaire. Votre but est d'obtenir la matrice identité dans la partie gauche de la matrice augmentée. Toutes les opérations que vous ferez à gauche, vous devrez les faire à droite, c'est-à-dire dans la matrice identité. Si les calculs sont simples, l'échelonnement est un peu complexe [7] .
    • Cet algorithme de Gauss-Jordan repose sur des échanges de lignes, la multiplication d'une ligne par un scalaire non nul et l'ajout, positif ou négatif, du multiple d'une ligne à une autre ligne. Nombreux sont les sites à exposer en détail cet algorithme.
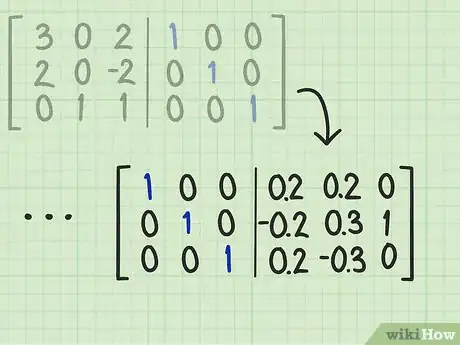
  3. Image intitulée Find the Inverse of a 3x3 Matrix Step 8
    3
    Continuez ainsi jusqu'à obtenir la matrice identité. Cet algorithme repose sur des itérations successives, le but étant de voir apparaitre la matrice identité à gauche (des 1 en diagonale et des 0 partout ailleurs). Quand cela sera fait, la matrice à droite du trait vertical sera la matrice inverse recherchée [8] .
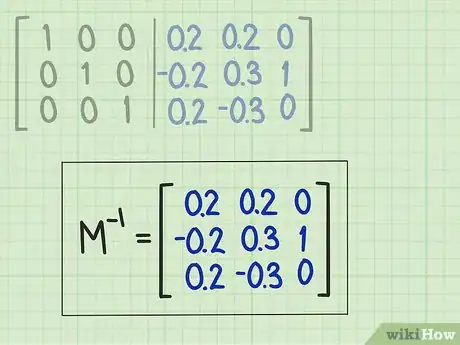
  4. Image intitulée Find the Inverse of a 3x3 Matrix Step 9
    4
    Recopiez la matrice inverse. Sur votre feuille définitive, récupérez cette matrice inverse et présentez-la comme une matrice normale, avec ses deux accolades [9] .
    Publicité

Méthode 3
Méthode 3 sur 3:
Se servir d'une calculatrice pour trouver une matrice inverse

  1. Image intitulée Find the Inverse of a 3x3 Matrix Step 10
    1
    Récupérez une calculatrice ayant une fonctionnalité matricielle. Autant dire qu'il vous faut une calculatrice un peu sophistiquée. Prenez-en une qui soit assez puissante, la TI-83 ou la TI-86 (Texas Instruments), étant donné qu'il y a un grand nombre de calculs à faire pour trouver la matrice inverse [10] .
  2. Image intitulée Find the Inverse of a 3x3 Matrix Step 11
    2
    Entrez votre matrice dans la machine. Dans un premier temps, il faut activer la fonction des matrices. Reportez-vous à la notice de votre calculatrice. Sur les calculatrices Texas Instruments, vous devez appuyer sur les touches 2nde, puis x-1.
  3. Image intitulée Find the Inverse of a 3x3 Matrix Step 12
    3
    Sélectionnez le sous-menu d'édition. En haut de l'écran, vous verrez différents menus. Sur une calculatrice Texas Instruments, à l'aide des touches de navigation, mettez le menu Edit en surbrillance. Cette opération varie selon le type de votre calculatrice. En cas de problème, reportez-vous à la notice de votre calculatrice [11] .
  4. Image intitulée Find the Inverse of a 3x3 Matrix Step 13
    4
    Donnez un nom à votre matrice. La plupart des calculatrices vous proposeront de choisir une lettre, souvent de A à J, pour nommer votre matrice. Si vous n'en avez qu'une à traiter, choisissez [A]. Une fois le nom choisi, validez-le en appuyant sur la touche entrer [12] .
  5. Image intitulée Find the Inverse of a 3x3 Matrix Step 14
    5
    Entrez les dimensions de votre matrice. Avec notre exemple, nous prendrons une matrice 3x3, tout en sachant qu'une calculatrice est capable de traiter des matrices bien plus grandes. Entrez le nombre de lignes, validez, entrez le nombre de colonnes et validez une deuxième fois [13] .
  6. Image intitulée Find the Inverse of a 3x3 Matrix Step 15
    6
    Entrez les valeurs de la matrice. Si tout s’est bien passé, sur votre écran, vous avez une matrice vide. Si vous avez déjà entré une ou plusieurs autres matrices, elles apparaitront également à l'écran. Le curseur met en surbrillance le premier élément de la matrice. Tapez simplement la valeur voulue, puis validez avec la touche entrer. Le curseur se déplacera alors sur l'élément suivant. Si une valeur est déjà inscrite, celle que vous rentrerez écrasera la précédente [14] .
    • Pour entrer une valeur négative, vous devez utiliser la touche des nombres négatifs, non le signe opératoire « - ». Si vous vous trompez de touche, la machine renverra un message d'erreur.
    • Vous pouvez entrer les éléments de la matrice dans l'ordre que vous voulez grâce aux flèches de navigation.
  7. Image intitulée Find the Inverse of a 3x3 Matrix Step 16
    7
    Quittez la fonction matricielle. Une fois tous les éléments de la matrice entrés dans la calculatrice, sur une calculatrice Texas Instruments, appuyez sur les touches 2nde, puis quitter. Vous sortez alors de la fonction matricielle et vous vous retrouvez sur l'écran classique de votre calculatrice [15] .
  8. Image intitulée Find the Inverse of a 3x3 Matrix Step 17
    8
    Utilisez la touche inverse pour avoir la matrice inverse. Dans un premier temps, retournez sur la fonction matricielle, amenez le curseur sur la rubrique Noms et choisissez la matrice en question (on dira la matrice A). Cela fait, appuyez sur la touche de l'inverse x-1. Selon les calculatrices, il faudra ou non appuyer au préalable sur la touche 2nde. Votre écran affiche désormais la mention . Appuyez sur la touche entrer et votre matrice inverse apparaitra à l'écran [16] .
    • N'utilisez pas la touche ^ pour inscrire sans quoi, votre calculatrice vous renverra une erreur.
    • Si après avoir appuyé sur la touche de l'inverse et si votre matrice a été correctement entrée, la calculatrice renvoie un message d'erreur, c'est que votre matrice n'a pas d'inverse. Vérifiez le déterminant.
  9. Image intitulée Find the Inverse of a 3x3 Matrix Step 18
    9
    Ajustez les coefficients de la matrice inverse. En effet, vous les voyez apparaitre sous une forme décimale, ce qui n'est pas très juste. Pour être précis, il faut présenter les coefficients sous forme fractionnaire, non calculés donc. Pour cela, il faut utiliser l'instruction Frac. Certes, c'est rare, mais il peut arriver que vous ayez du premier coup une matrice inverse ne comprenant que des entiers [17] .
    • Si votre calculatrice peut gérer les matrices, elle a forcément une fonction lui permettant de convertir les décimales en fractions. Sur une calculatrice TI-86, activez la fonction Math, puis optez pour Misc et enfin Frac. Validez avec la touche entrer : les valeurs décimales ont été remplacées par des fractions.
  10. Image intitulée Calculate Total Cost Step 1
    10
    Pensez aux touches crochets. La majorité des calculatrices graphiques ont aussi des touches crochets (par exemple, sur la TI-84, c'est 2e et x et 2e et -) qui peuvent être utilisées pour écrire dans une matrice sans utiliser la fonction de matrice. Remarque : la calculatrice ne formatera pas la matrice tant que la touche entrée/égal n'aura pas été utilisée (c'est-à-dire que tout se trouvera sur une ligne et ce ne sera pas joli).
    Publicité

Conseils

  • La méthode exposée ici marche aussi pour les matrices qui contiennent des inconnues ou des expressions algébriques, le principe est le même.
  • Écrivez toutes les étapes, car l'inversion d'une matrice 3x3 de tête est extrêmement difficile.
  • Il existe des programmes informatiques qui permettent de calculer les matrices inverses, jusqu'à trente lignes et colonnes.
  • Quelle que soit la méthode choisie, vérifiez que votre résultat est bon. Pour cela, multipliez M et M-1. La théorie veut que : M x M-1 = M-1 x M = I, I étant la matrice identité, c'est-à-dire une matrice dans laquelle la diagonale est constituée de 1, les autres valeurs étant des 0. Si ce n'est pas le cas, c'est que vous avez commis une erreur à un moment donné.
Publicité

Avertissements

  • Il est des matrices 3x3 qui n'ont pas d'inverse. C'est ce qui arrive quand le déterminant de la matrice est nul. Dans la formule, vous avez remarqué qu'il fallait diviser par le déterminant et si celui-ci est nul, l'opération n'est tout simplement pas possible.
Publicité

wikiHows en relation

calculer un pourcentage d'augmentation
Comment
calculer un pourcentage d'augmentation
calculer le diamètre d'un cercle
Comment
calculer le diamètre d'un cercle
calculer la hauteur d'un triangle
Comment
calculer la hauteur d'un triangle
calculer la valeur de résistances en série ou en dérivation
Comment
calculer la valeur de résistances en série ou en dérivation
calculer un écart type
Comment
calculer un écart type
calculer le déterminant d'une matrice 3 x 3
Comment
calculer le déterminant d'une matrice 3 x 3
calculer le rayon d’un cercle
Comment
calculer le rayon d’un cercle
calculer la diagonale d’un rectangle
Comment
calculer la diagonale d’un rectangle
calculer la longueur de l'hypoténuse
Comment
calculer la longueur de l'hypoténuse
calculer un intervalle de confiance
Comment
calculer un intervalle de confiance
calculer les probabilités de gagner à la loterie
Comment
calculer les probabilités de gagner à la loterie
calculer une racine carrée à la main
Comment
calculer une racine carrée à la main
calculer l’angle entre deux vecteurs
Comment
calculer l’angle entre deux vecteurs
calculer une moyenne pondérée
Comment
calculer une moyenne pondérée
Publicité

Références

  1. ↑ https://www.mathsisfun.com/algebra/matrix-inverse-minors-cofactors-adjugate.html
  2. ↑ http://www.mathcentre.ac.uk/resources/uploaded/sigma-matrices11-2009-1.pdf
  3. ↑ http://www.mathwords.com/c/cofactor_matrix.htm
  4. ↑ http://www.mathwords.com/c/cofactor_matrix.htm
  5. ↑ http://mathworld.wolfram.com/MatrixInverse.html
  6. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  7. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  8. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  9. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  1. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  2. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  3. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  4. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  5. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  6. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  7. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
  8. ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html

À propos de ce wikiHow

l'équipe de wikiHow
Coécrit par:
l'équipe de wikiHow
Rédacteurs de wikiHow
Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.

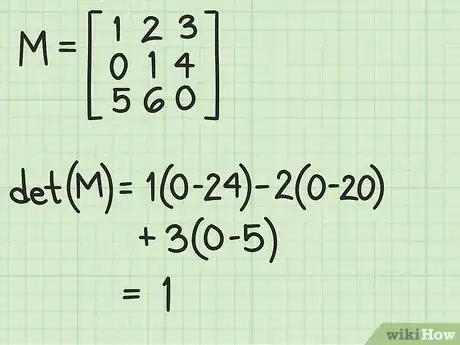
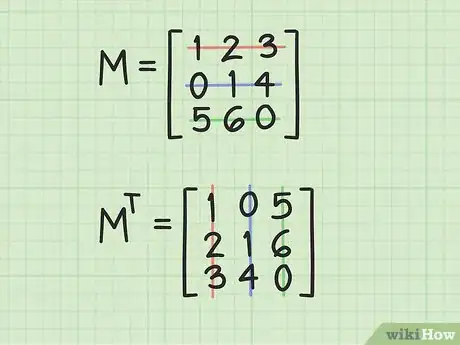
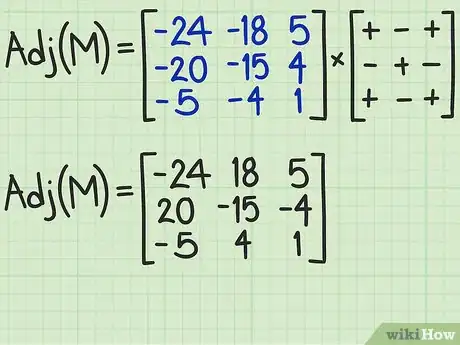
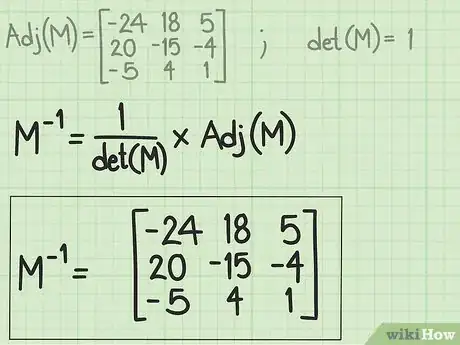
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 674 708 fois.
Catégories: Calculs
Publicité