Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 131 529 fois.
Les probabilités sont une branche complexe des mathématiques, mais tout le monde les connait, comme celle qui consiste à savoir quelles sont vos chances de gagner au LOTO. Sans forcément les connaitre précisément et savoir ce que cela représente, des centaines de milliers de personnes jouent au LOTO, sachant pertinemment que la probabilité de gagner au 1er rang (5 numéros et numéro chance) est extrêmement faible. Avant de jouer, il est peut-être intéressant de connaitre ses probabilités de gagner… et de perdre !
Étapes
Méthode 1
Méthode 1 sur 3:Calculer la probabilité de gagner au 1er rang
-
1Comprenez bien la formule de probabilité. La probabilité de gagner () au LOTO est conditionnée par deux nombres : celui des numéros proposés par le prestataire () et celui des numéros choisis par le joueur (). À tout moment du tirage, tout numéro a la même probabilité de sortir (équiprobabilité). Il existe une formule immuable pour connaitre la probabilité de gagner : . Cette formule permet de calculer le rapport entre les combinaisons jouées et celles possibles. Le signe à gauche d'un nombre () désigne sa factorielle. équivaut au produit de toutes les valeurs inférieures ou égales à ( [1] ).
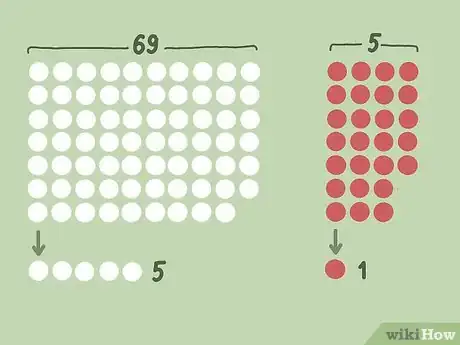
- Pour commencer en douceur, imaginons que vous deviez trouver la probabilité de tirer deux bons numéros parmi les chiffres de 1 à 5. Conformément à la formule présentée ci-dessus, cette probabilité est de .
- Développons cette fraction et cela donne : .
- En résumé, la probabilité de trouver les deux bons numéros parmi 5 est de 1 sur 10.
- Tant que la factorielle est petite, le calcul est simple, beaucoup moins quand on dépasse la factorielle 10. Heureusement, il existe une touche sur les calculatrices scientifiques et si vous tapez 55! dans Google, vous obtiendrez immédiatement la réponse.
-
2Connaissez les règles du LOTO. Le jeu est simple : vous devez cocher 6 numéros, à savoir 5 sur une grille de 49 numéros, et 1 numéro chance sur une grille de 10. Lors du tirage (il y en a 3 par semaine), 5 boules numérotées sont tirées devant huissier, puis une dernière boule (numéro chance) est tirée d'une autre sphère, c'est un tirage complémentaire. Pour l'EuroMillions, deux tirages par semaine, le principe est le même, à savoir 5 numéros parmi 50 et deux étoiles numérotées parmi 12 [2] .
- En fait, peu importe les supports de tirages pour le calcul des probabilités, ce qui compte, c'est qu'un numéro tiré n'est jamais remis en jeu. Dans cette perspective, il faut connaitre le nombre de numéros de la grille et celui des numéros tirés et donc à cocher [3] .
-
3Faites l'application numérique. Pour le LOTO simple, 5 boules sont tirées au sort l'une après l'autre depuis une sphère qui en contient 49, toutes ayant la même probabilité (variable après chaque tirage) de sortir. La probabilité de trouver la bonne combinaison s'établit donc à une chance sur , soit 1 chance sur
. -
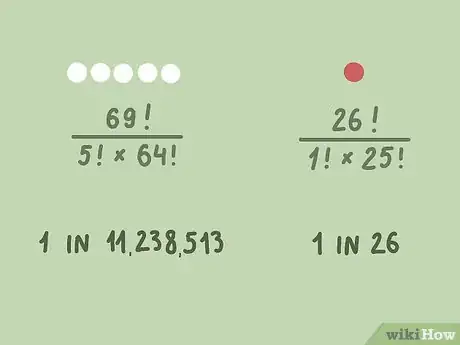
4Ne faites pas d'erreurs dans le calcul. Avec deux factorielles (49! et 44!), mieux vaut prendre une calculatrice scientifique, une calculatrice en ligne ou Google (vous tapez la factorielle telle quelle). Au LOTO, la probabilité établit que vous avez une chance sur 1 906 884 (0,000 052 44 %) de trouver la bonne combinaison de 5 numéros (soit le 2e rang) : reconnaissons que c'est faible, non !
- Sous la grille principale est une seconde grille avec seulement 10 numéros (de 1 à 10). Le cochage d'un des numéros est compris dans les 2,20 € du prix de la grille. C'est le numéro chance et sa probabilité de sortie est assez simple, puisqu'il n'y a pas ici de combinaisons : votre numéro chance a 1 chance sur 10 de sortir. Pour les puristes, nous aurions pu utiliser la formule
(), mais c'est tellement évident ici.
- Sous la grille principale est une seconde grille avec seulement 10 numéros (de 1 à 10). Le cochage d'un des numéros est compris dans les 2,20 € du prix de la grille. C'est le numéro chance et sa probabilité de sortie est assez simple, puisqu'il n'y a pas ici de combinaisons : votre numéro chance a 1 chance sur 10 de sortir. Pour les puristes, nous aurions pu utiliser la formule
-
5Multipliez les deux probabilités pour gagner au 1er rang. Ce que l'on appelle le 1er rang est la découverte des 5 premiers numéros et du numéro chance. Quelle est dès lors la probabilité de gagner au 1 er rang ? Il suffit de multiplier les deux probabilités. Pour les 5 numéros, elle était de et pour le numéro chance de . Pour avoir les six numéros, la probabilité est de : [4] .
- Si vous voulez gagner la plus grosse somme en jeu, il vous faudra jouer les
19 068 840 combinaisons possibles à 2,20 €, soit 41 951 448 € à débourser !
Publicité - Si vous voulez gagner la plus grosse somme en jeu, il vous faudra jouer les
Méthode 2
Méthode 2 sur 3:Calculer la probabilité de gagner aux autres rangs
-
1Calculez la probabilité de gagner au 2e rang. Gardons le LOTO comme exemple. Vous avez eu 5 numéros, mais il vous manque le numéro chance : vous gagnez au 2e rang ! Et c'est intéressant aussi ! Tout comme nous avons pu calculer la probabilité de gagner au 1er rang, il est possible de connaitre celle du 2e rang. En fait, nous la connaissons déjà, puisqu'il s'agit de la probabilité de la première grille, soit 1 chance sur 1 906 884 de la trouver [5] .
- Si vous remportez le 2e rang, c'est que vous n'avez pas trouvé le numéro chance. Comme ce dernier est tiré à part, il n'a aucune influence sur votre chance de gagner au 2e rang, mais de façon assez tordue, l'on pourrait dire que pour gagner au 2e rang, il vous faut ne pas trouver le numéro chance (9 chances sur 10) !
- Théoriquement, pour connaitre la probabilité de gagner au 2e rang, vous devez multiplier celle d'avoir les 5 numéros () par celle de ne pas avoir choisi le bon numéro chance (), soit 1 chance sur 2 118 760.
-
2Servez-vous d'une formule pour tous les gains possibles. Vous l'avez compris, il est possible de calculer toutes les probabilités des gains fixés par l'organisateur du jeu. La formule littérale des probabilités de gains est la suivante :
, formule dans laquelle représente le nombre de numéros gagnants que vous voulez, est le nombre total des numéros tirés au sort et le nombre de numéros en jeu (boules dans la sphère).- Vous avez abandonné l'idée de gagner au 1 er rang, mais vous visez le 6e rang à 3 numéros. Cherchons les chances de gagner avec 3 bons numéros sur 5 joués sur une grille classique de LOTO contenant 49 numéros. La formule devient alors la suivante : .
- La première partie de la formule est la probabilité d'avoir 3 numéros parmi les 5 gagnants, tandis que la seconde partie, vous la connaissez bien maintenant, est la probabilité d'avoir 5 bons numéros parmi les 49.
-
3Faites les calculs de probabilité. Comme précédemment, à cause des factorielles, il est mieux de recourir à une calculatrice scientifique avec touche dédiée ou à une calculatrice en ligne. Certains calculs intermédiaires sont complexes, et toute erreur d'entrée ou de transcription des résultats entrainerait une probabilité fausse [6] .
- Pour en revenir à la probabilité de sortir 3 numéros gagnants sur une combinaison de 5 sur 49 numéros possibles, elle s'élève à 1 sur 9 458.
-
4Multipliez ce résultat par la probabilité du numéro chance. Cette formule vous permet de connaitre la probabilité de jouer la bonne combinaison à tel ou tel rang sans tenir compte du tirage du numéro chance. Partant, si vous voulez en tenir compte, vous devez multiplier cette probabilité par celle d'avoir (rangs impairs de 1 à 9) ou de ne pas avoir le numéro chance (rangs pairs de 2 à 8 [7] ).
- Vous voulez savoir quelle est la probabilité de gagner en ayant 3 bons numéros sans le numéro chance (probabilité s'établissant à 9:10), alors la formule se présente ainsi : , soit 1 chance sur 224.
- En parallèle, la probabilité d'avoir trois bons numéros et le numéro chance s'établit avec la formule ainsi remplie : , soit 1 chance sur
2 016.
-
5Changez k pour calculer les probabilités des autres rangs. La formule reste la même, vous n'avez plus qu'à changer la variable k pour savoir quelles sont vos chances de gagner à 4, à 3 (c'est fait !) ou à 2 numéros. Les chances de gagner diminuent quand augmente, et la diminution des chances est tout, sauf arithmétique [8] .
- Pour un tirage de numéros couplé à un tirage annexe, n'oubliez pas de multiplier la probabilité du tirage principal par celle du tirage annexe afin d'obtenir la probabilité globale.
Publicité
Méthode 3
Méthode 3 sur 3:Évaluer autrement ses chances de gagner au LOTO
-
1Trouvez le taux de redistribution (ou de retour) du LOTO. Ce taux de retour au joueur (TRJ) est la proportion globale des mises qui revient aux joueurs sous forme de gains. Au LOTO, ce taux est assez stable autour de 50 à 53 % des sommes jouées : pour chaque grille à 2,20 €, si tout le monde gagnait la même somme, chaque grille rapporte environ 1,10 €. Peu incitatif [9] !
- Pour d'autres jeux de la FDJ, les taux de retour sont plus importants. Au Keno, le TRJ est de 63 % : avec une grille à 10 €, vous risquez de toucher en retour 6,30 €.
- Il va de soi que ce taux de retour joueur est calculé sur l'ensemble des joueurs sur le long terme : votre propre taux de retour est souvent inférieur…, sauf si vous gagnez gros !
-
2Comparez le prix d'une grille et son taux de retour. En matière de jeux existe la notion d'espérance de gain qui s'obtient en comparant, dans le cas du LOTO, le prix d'une grille et le taux de retour du jeu. Comme l'organisateur du jeu ne fonctionne pas à perte, le taux de retour est toujours inférieur au prix de la grille. Ne confondez pas le taux de retour global (ensemble des joueurs) et le vôtre. Ces taux de retour moyen et individuel ne coïncident jamais. Selon la loi des grands nombres, dans la majorité des cas, vous ne toucherez même pas ce taux moyen, et dans de très rares cas, vous toucherez soit une grosse somme, soit rien [10] .
- Si beaucoup jouent pour le plaisir sans plan préconçu, à fonds perdu, dans l'espoir de peut-être rentrer dans leurs mises, d'autres étudient avec attention cette fameuse espérance de gain et misent sur des jeux qui ont les meilleures espérances, en quelque sorte les meilleurs retours sur investissement [11] .
-
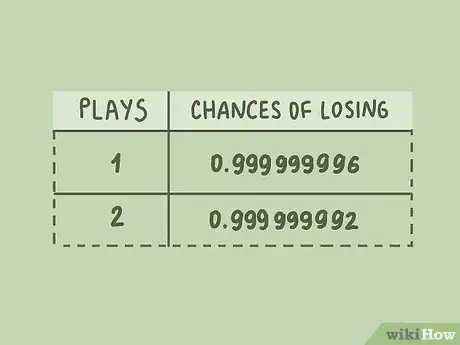
3Déterminez la probabilité de gagner en jouant en multiple. Par cette expression, nous entendons le jeu de plusieurs grilles pour un même tirage. Comme la probabilité générale est toujours le produit des probabilités individuelles, par un raisonnement un peu abscons, vous avez ainsi moins de chances de perdre, mais pas plus de gagner [12] .
- Si à un jeu, vous avez, par exemple, une chance de gagner sur 250 000 000, cela signifie dans la même logique que vous avez 99,99… % (pourcentage obtenu en calculant ) de risque de perdre.
- Si vous jouez deux fois au même tirage, le risque de perdre est moins élevé, puisque vous élevez au carré le risque à un tirage, soit
, et si l'on peut le dire ainsi, une plus grande chance de gagner !
-
4Déterminez le nombre de jeux nécessaire pour gagner. Sous-entendu, pour gagner même le plus petit lot. Beaucoup de joueurs pensent qu'en jouant plus et plus souvent, ils augmentent leurs chances de gagner. C'est vrai sur le papier et à la condition de participer systématiquement à tous les tirages et de ne pas tenir compte du montant des gains : comprenez vous gagnerez, mais pas forcément de gros lots [13] .
- Imaginons un jeu avec lequel il y aurait 1 chance sur 250 000 000 de gagner le prix le plus élevé, il vous faudrait jouer 180 millions de grilles pour que la probabilité tombe à 1chance sur 2.
- Traduit en durée : faites 10 grilles par jour pendant 49 300 ans et vous aurez cette chance sur 2 de gagner le gros lot.
- Ce pourcentage de 50 % est trompeur, car au bout de ces 49 300 ans (c'est long !), si vous achetez vingt tickets, la probabilité de gagner se maintient 1 chance sur 2… à quelques décimales près !
Publicité
Conseils
- Dans une loterie de ce type, toute combinaison a la même chance de sortir : 32-45-22-19-09-11 a autant de chances de sortir que 1-2-3-4-5-6.
Avertissements
- Ne misez pas plus que ce que vous êtes capable de gagner par votre travail !
- « Jouer comporte des risques : endettement, isolement, dépendance… » affirme le slogan de Joueurs Info Service. Cet organisme est là pour vous aider au cas où vous auriez un problème d'addiction aux jeux.
- Ne vous laissez pas abuser par ces courriels ou ces publicités sur Internet qui vous promettent, moyennant rémunération, grâce à leurs méthodes, de gagner à tout coup. S'il y en a qui gagnent, ce sont bien ces truands !
Références
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ https://www.wired.com/2016/01/the-fascinating-math-behind-why-you-wont-win-powerball/
- ↑ https://www.wired.com/2016/01/the-fascinating-math-behind-why-you-wont-win-powerball/
- ↑ http://wmbriggs.com/post/5285/
- ↑ http://www.quickanddirtytips.com/education/math/what-are-the-odds-of-winning-the-lottery
- ↑ http://www.quickanddirtytips.com/education/math/what-are-the-odds-of-winning-the-lottery










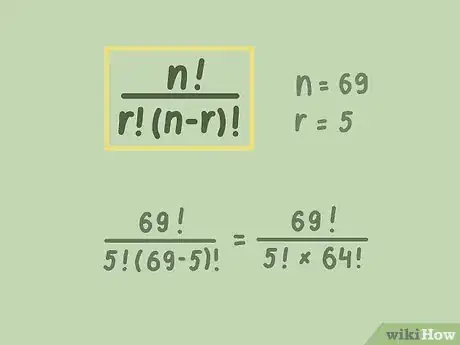









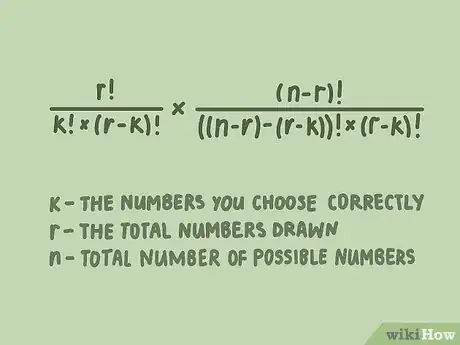







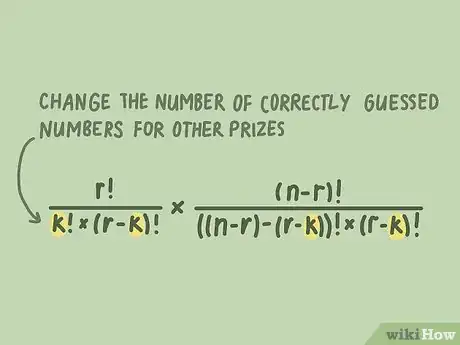
























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 131 529 fois.