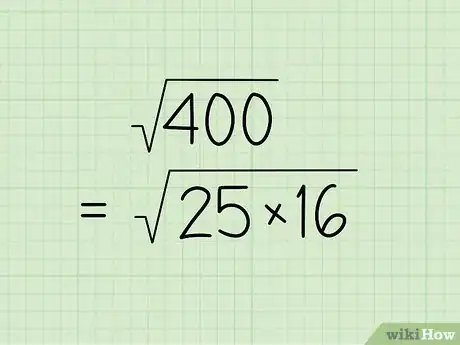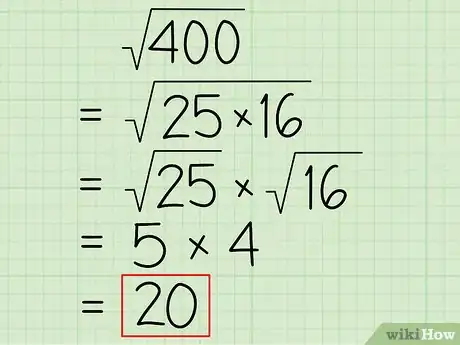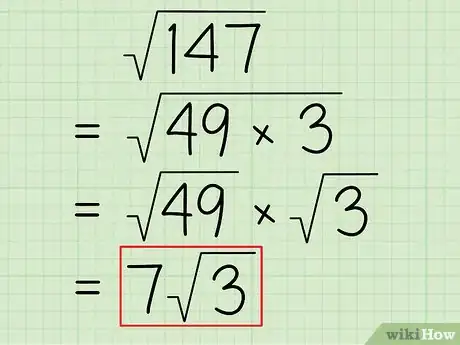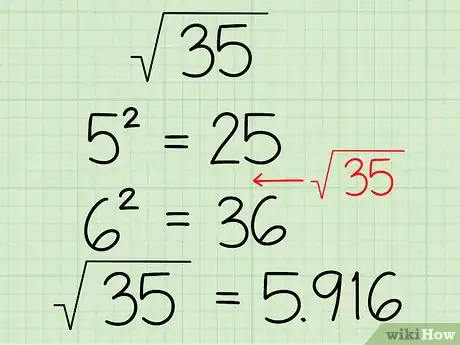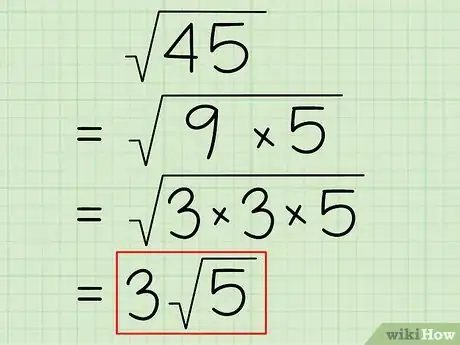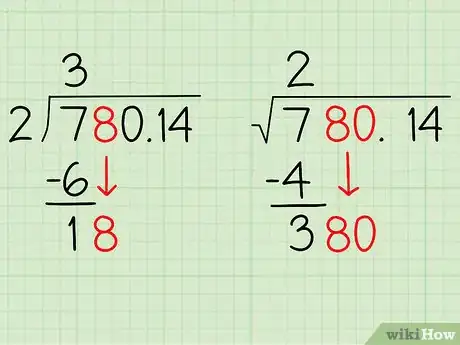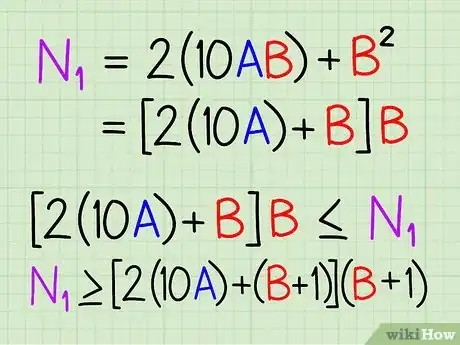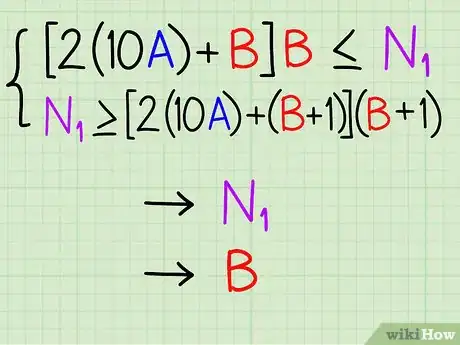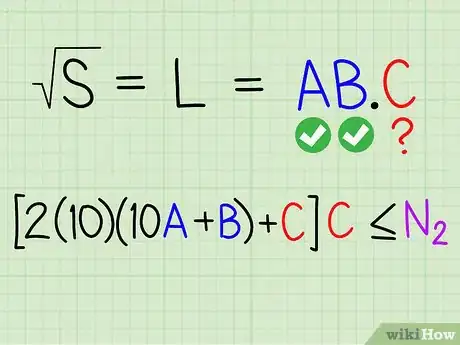Comment calculer une racine carrée à la main

Informations concernant l'auteur.e

Avant que n'arrivent les calculatrices et autres ordinateurs, on était bien obligé de calculer les racines carrées à la main, c'est ce que faisaient les étudiants et leurs professeurs. Il existe différentes méthodes pour calculer la racine carrée d'un nombre à la main. Alors que certaines méthodes ne vous donneront qu'un résultat approché, d'autres permettent d'obtenir une précision remarquable.

Méthode 1

Méthode 1 sur 2:
Utiliser la décomposition en facteurs

1
Essayez de décomposer votre nombre en facteurs qui sont des carrés parfaits. Cette méthode s'appuie sur la décomposition en facteurs, dont on prendra la racine de chacun d'eux (le résultat final sera soit un entier soit une valeur approchée). Les facteurs d'un nombre sont les nombres ou les chiffres qui, multipliés entre eux, donnent le nombre en question ^{[1]
X
Source de recherche}. Ainsi, les facteurs de 8 sont 2 et 4, car 2 x 4 = 8. Les carrés parfaits, quant à eux, sont des nombres qui sont le produit de deux nombres identiques Ainsi, 25, 36 et 49 sont des carrés parfaits parce qu'ils correspondent respectivement à 5², 6² et 7². Les facteurs qui sont des carrés parfaits, comme vous pouvez l'imaginer, sont des facteurs d'un nombre tout en étant des carrés parfaits. Pour cette méthode, le point de départ consiste à décomposer un nombre en facteurs qui sont des carrés parfaits.
- Prenons un exemple. On va chercher la racine carrée de 400. En premier lieu, on va décomposer ce nombre en facteurs qui sont des carrés parfaits. 400 est un multiple de 100, mais c'est aussi un multiple de 25, un carré parfait. Mentalement, on sait que 400 = 25 x 16. Or, 16, étrangement, est aussi un carré parfait. En conséquence, les facteurs de 400, qui sont aussi des carrés parfaits, sont 25 et 16, puisque 25 x 16 = 400.
- On peut dès lors écrire l'égalité suivante : √(400) = √(25 x 16).
2
Calculez la racine de chacun des « facteurs-carrés parfaits ». Il est établi que, pour tout nombre a et b, on a : √(a x b) = √(a) x √(b) ^{[2]
X
Source de recherche}. Grâce à cette propriété, Il suffit de calculer les racines et de multiplier entre eux les résultats obtenus.
- Dans notre exemple, on calcule les racines de 25 et de 16, ce qui nous donne :
  - √(25 x 16)
  - √(25) x √(16)
  - 5 x 4 = 20
3
Bien sûr, c'est là le cas idéal. Le plus souvent, il n'est pas possible de décomposer un nombre en un produit de carrés parfaits (400 est un cas vraiment exceptionnel !) À ce moment-là, il faut extraire le ou les carrés parfaits qui composent votre nombre et réduire l'ensemble à sa plus simple expression. On ne trouvera donc pas comme réponse un entier. Réduire une racine permet de mieux la manipuler ensuite. Donc, avec un nombre quelconque, on le décompose en un produit de carrés parfaits et de nombres quelconques.
- Prenons comme exemple la racine carrée de 147. Ce nombre n'est pas le produit de 2 carrés parfaits. Le résultat qu'on obtiendra ne sera donc pas un entier. Pourtant 147 est bien le produit d'un carré parfait - 49 - et d'un nombre quelconque - 3 - Pourtant on peut réduire la racine de 147, ce qui donne ceci :
  - √(147)
  - = √(49 x 3)
  - = √(49) x √(3)
  - = 7 x √(3) = 7√(3)
4
Si on vous le demande, faites le calcul. À partir de votre racine réduite à sa plus simple expression, il est plus facile d'en estimer la valeur chiffrée en devinant la valeur de la racine restante. Pour cela, on encadre cette racine par les carrés parfaits proches et l'on essaie d'affiner par intuition et déduction.
- Reprenons notre exemple. Comme 2² = 4 et que 1² = 1, nous pouvons en déduire que √(3) se situe entre 1 et 2 - probablement plus proche de 2 que de 1. Estimons-la à 1,7. Donc, on fait 7 x 1,7 = 11,9. Quand on calcule de façon plus juste, avec une calculatrice, par exemple, on obtient 12,13. On n'était pas très loin !
  - Cela marche aussi pour des nombres plus grands. Par exemple, √(35) doit être entre 5 et 6 (probablement plus proche de 6). 5² = 25 et 6² = 36. 35 est donc bien entre 25 et 36 et sa racine est donc entre 5 et 6. Comme 35 vient juste avant 36, la réponse doit être très proche de 6. Avec une calculatrice, on trouve environ 5,92 - c'est bon !
5
Sinon, vous faites la décomposition comme ci-dessus. Ensuite, il n'est pas toujours obligatoire de chercher les carrés parfaits : on peut tout décomposer en facteurs premiers. Là, il est possible, par le jeu des décompositions, de trouver des facteurs qui apparaissent deux fois. Repérez toutes ces « paires » de facteurs premiers. Si votre décomposition fait apparaitre 2 facteurs premiers identiques, vous les retirez tous les deux de la racine et vous en mettez un devant la racine.
- Prenons le cas de la racine carrée de 45 en utilisant cette méthode. On sait que 45 = 9 x 5 et que 9 = 3 x 3. Partant de là, on peut récrire la racine avec la décomposition en facteurs premiers : √(3 x 3 x 5). Pour réduire la racine à sa plus simple expression, il faut retirer les deux 3 de la racine et en mettre un devant la racine : 3√(5). Désormais, vous pouvez facilement donner une valeur approchée.
- Prenons un dernier exemple : essayons de trouver la racine carrée de 88 :
  - √(88)
  - = √(2 x 44)
  - = √(2 x 4 x 11)
  - = √(2 x 2 x 2 x 11). Il y a plusieurs 2 et comme c'est un nombre premier, on ne peut décomposer davantage. On va pouvoir sortir une paire de 2 de dessous la racine et mettre 2 devant la racine.
  - Réduite à sa plus simple expression, la racine donne : 2 √(2 x 11) ou encore 2 √(2) √(11). À ce stade, vous pouvez calculer la valeur approximative de votre racine en estimant √(2) et √(11) et en multipliant le tout par 2.
Publicité

Méthode 2

Méthode 2 sur 2:
Trouver une racine carrée à la main

Utiliser la division

1
Groupez les chiffres de votre nombre en paires. On va faire une sorte de division classique, mais elle est un peu différente quand même ! On va trouver la racine carrée exacte, chiffre après chiffre. Pour être plus efficace, vous allez vous construire un cadre de division et découper votre nombre en tranches de deux chiffres (paires). En premier lieu, tracez une ligne verticale qui sépare votre feuille en deux parties égales, puis tracez une petite ligne horizontale, dans la partie de droite. Cette ligne sera mise vers le haut. Vous obtenez ainsi un petit espace en haut et un plus grand en bas. Enfin, divisez votre nombre en tranches de deux chiffres en commençant à la virgule. Selon ce principe, 79 520 789 182,47897 devient « 7 95 20 78 91 82, 47 89 70 ». Inscrivez votre nombre dans le coin supérieur gauche.
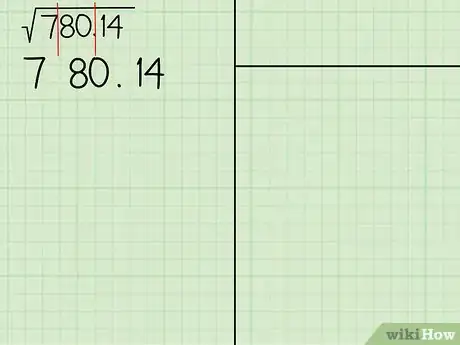
- À titre d'exemple, calculons la racine carrée de 780,14. Divisez votre espace à l'aide de deux lignes et inscrivez « 7 80, 14 » en haut à gauche. Vous le remarquez, il y a une tranche à gauche qui n'a qu'un chiffre : ce n'est pas grave, c'est normal ! Vous inscrirez votre réponse (c'est-à-dire la racine carrée de 780,14) en haut à droite.
2
Trouvez le plus grand entier n dont le carré est inférieur ou égal à la paire la plus à gauche. En effet, on commence toujours avec la « tranche » (paire) le plus à gauche, que ce soit une paire ou pas. Trouvez le plus grand carré est inférieur ou égal à cette paire et prenez la racine carrée de ce carré parfait. Ce nombre, c'est n. Inscrivez n en haut à droite et inscrivez son carré (n²) en bas à droite de la division.
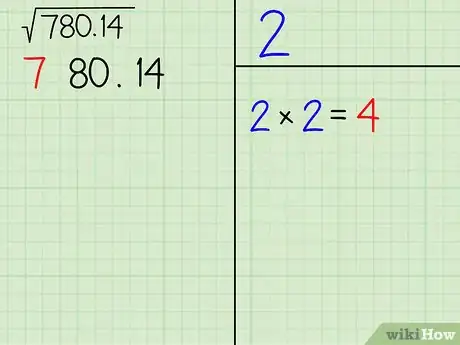
- Dans notre exemple, la « tranche » (paire) le plus à gauche est 7. Nous savons que : 2² (= 4) ≤ 7 < 3² (= 9), on peut alors dire que n = 2, car c'est le plus grand entier dont le carré est inférieur ou égal à 7. Inscrivez 2 dans le secteur supérieur droit. C'est le premier chiffre de votre réponse finale. Inscrivez 4 (carré de 2) en bas à droite de la division. Ce nombre aura son importante à la prochaine étape.
3
Soustrayez le nombre que vous venez de calculer de la paire la plus à gauche. Ce carré que vous venez de calculer, vous devez le retrancher de la tranche de départ. Inscrivez ce nombre juste sous la première tranche et faites la soustraction. Inscrivez les résultats en dessous.
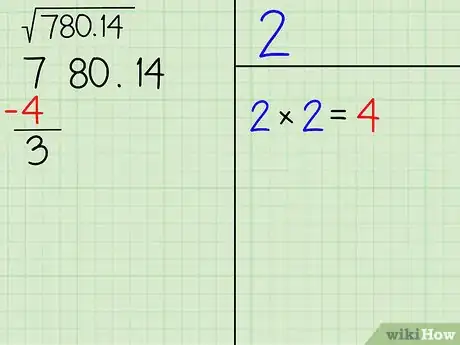
- Dans notre exemple, il faut écrire 4 sous le 7 et faire la soustraction, ce qui nous donne 3.
4
Abaissez la prochaine paire. Il faut maintenant abaisser au niveau du 3 de la soustraction la paire suivante, celle qui se trouve juste à gauche. Multipliez mentalement par 2 le nombre qui se trouve dans le coin supérieur droit de la division et inscrivez le résultat dans l'espace en bas à droite de la même division, en dessous de votre première ligne de calcul. Sur cette deuxième ligne, à côté du chiffre que vous avez mis, ajoutez '"_ x _="'
- Dans notre exemple, la prochaine paire est « 80 ». Inscrivez « 80 » à côté du reste qu'on a trouvé, soit le 3. On multiplie mentalement par 2 le nombre qui se trouve dans le coin supérieur droit de la division. Ici, c'est 2, donc 2 x 2 = 4. Inscrivez « 4 » en bas à droite, sur la deuxième ligne, puis on ajoute _ x _=
5
Reste à remplir les blancs. Ces deux « trous » doivent être remplis avec le même entier. La multiplication devra donner un résultat inférieur ou égal au nombre qui se trouve à gauche.
- Dans notre exemple, si on met par exemple 8, on obtient : 4(8) x 8 = 48 x 8 = 384. C'est plus grand que 380. 8 est donc trop grand, mais de peu. Essayons 7. On a donc : 4(7) x 7 = 329. Parfait ! 329 est inférieur à 380. Inscrivez alors 7 dans le secteur supérieur droit. C'est le second chiffre de votre résultat, la future racine carrée de 780,14.
6
Comme précédemment, soustrayez ce produit (en bas à droite) du nombre initial (à gauche). Posez l'opération et faites-la. Marquez le résultat.
- Dans notre exemple, vous devez ôter 329 de 380, ce qui nous donne 51.
7
Répétez l'étape 4. Abaissez la paire suivante du nombre initial. Quand vous allez arriver à la virgule, mettez une virgule dans le coin supérieur droit. On multiplie mentalement le nombre de ce coin-là par 2 et ce résultat, on l'inscrit dans la partie inférieure droite, sur la troisième ligne et on ajoute («_ x _ »).
- Dans notre exemple, on rencontre en effet la virgule de 780,14, donc, on en met une après le 27 en haut à droite. On abaisse à gauche la nouvelle paire -14 -. On multiplie 27 par 2, soit 54 qu'on inscrit dans la partie inférieure droite, sur la troisième ligne, ce qui nous donne : « 54 _ x _= ».
8
Répétez les étapes 5 et 6. Comme tout à l'heure, il reste à remplir les blancs. Ces deux « trous » doivent être remplis avec le même entier. La multiplication devra donner un résultat inférieur ou égal au nombre qui se trouve à gauche.
- Dans notre exemple, 549 x 9 = 4 941, ce qui est inférieur à 5 114. Il n'y a pas d'autre réponse possible ! Vous mettez donc un 9 dans le coin supérieur droit et vous ôtez 4 941 de 5 114 dans la partie gauche : 5 114 - 4 941 = 173.
9
Si vous devez continuer, il faut alors abaisser une paire de 0, puis répétez les étapes 4 ; 5 et 6. En fait, tout va dépendre de la précision que vous voulez ou qu'on vous a demandée. Chaque fois, vous abaisserez une paire de 0 et vous ferez les calculs.

Publicité

Comprendre comment cela fonctionne

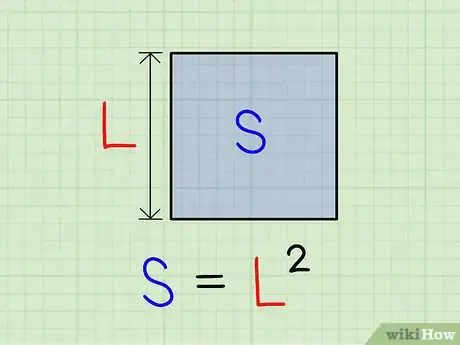
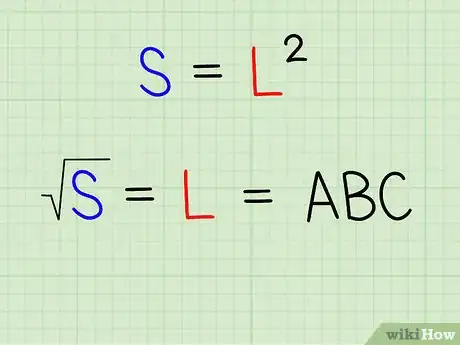
1
Imaginez le nombre dont vous cherchez la racine carrée comme la surface S d'un carré (la forme géométrique). Vous le savez, la surface d'un carré de côté L est L². Donc, trouver la racine carrée de votre nombre, c'est chercher le côté L d'un carré de surface L².
2
On appellera A le premier chiffre de L (la racine carrée que nous essayons de calculer). B sera le deuxième chiffre de L, C le troisième, etc.
3
Donnons également un nom à chaque tranche de S. On appellera Sa la première paire de chiffres de S, Sb la deuxième paire, etc.
4
Comprenez bien ce qu'est cette division particulière. On fait une vraie division, celle où le dividende est votre nombre de départ et où le diviseur est la racine carrée de ce même nombre. Ici, la différence avec une division « normale », c'est qu'au lieu de prendre un chiffre à la fois au dividende, on en prend deux (racine carrée oblige !) Sinon le principe reste le même !
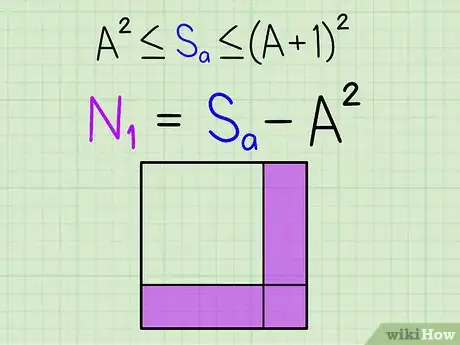
5
Trouvez le plus grand nombre dont le carré est inférieur ou égal à S_a. Le premier chiffre de votre racine, A, est le plus grand entier dont le carré n'est pas supérieur à S_a (A doit satisfaire l'inéquation suivante : A² ≤ Sa < (A+1)²). Dans notre exemple, S_a = 7 et 2² ≤ 7 < 3², donc A = 2.
- Cela fonctionne comme une division classique. Admettons que vous vouliez diviser 88962 par 7. Par quoi commencez-vous ? Vous cherchez combien il va de fois 7 (le diviseur) dans 8 (le premier chiffre du dividende). Mathématiquement, vous cherchez un entier d qui remplisse la condition suivante : 7×d ≤ 8 < 7×(d+1). ici, d vaudra 1.
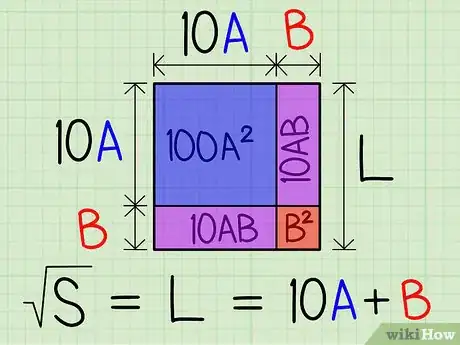
6
Visualisez bien ce carré dont la surface est en fait le nombre dont vous cherchez à calculer la racine. Votre réponse, la racine carrée de votre nombre de départ, est L, laquelle valeur est le côté du carré de surface S (votre nombre de départ). Les chiffres A, B et C sont les trois chiffres de notre valeur L. Si la réponse est un nombre compris entre 10 et 99, L= (10A) + B ; si la réponse est comprise entre 100 et 999, L = (100A) +10B + C, etc.
- Dans notre exemple, (10A+B)² = L² = S = 100A² + 2 x 10A x B + B². 10A+B est notre réponse L, A représentant les dizaines et B les unités. Ainsi, avec A=1 et B=2, 10A+B sera le nombre 12. (10A+B)² est la surface de tout le carré, 100A² est la surface du plus grand carré inscrit dans le grand, B² est la surface du plus petit carré inscrit dans le grand et 10A x B est la surface de chacun des deux rectangles restants pour compléter le carré de départ. Vous le voyez, on cherche à reconstituer le carré de départ par une approche successive, fait de carrés et de rectangles intermédiaires.
7
Ôtez A² de S_a. Abaissez une paire (S_b) à partir de S. S_a S_b constituent presque la surface totale du carré de base, donc soustrayez la surface du grand carré à l'intérieur du carré. Ce qui reste est le nombre N1 obtenu à gauche lors de l'étape 4 (N1 = 380 dans notre exemple). N1 est égal à 2 x 10A x B + B² (surface des deux rectangles + surface du petit carré).
8
Cherchez N1 = 2×10A×B + B², qu'on peut aussi écrire : N1 = (2×10A + B) × B. Dans notre exemple, vous avez déjà N1 (380) et A (2) : ne reste plus qu'à trouver B ! À l'évidence, B ne sera pas un entier, donc vous devez trouver l'entier B qui remplit la condition suivante : (2×10A + B) × B ≤ N1. On a au final : N1 < (2×10A + (B+1)) × (B+1)).
9
Faites les calculs. Pour résoudre cette équation, multipliez A par 2, placez-le dans la position du nombre des dizaines (ce qui revient à multiplier le résultat par 10), placez B dans la position du nombre des unités et multipliez le nouveau résultat par B. Ce nombre est donc : (2x10A + B) x B, et cela correspond exactement à ce que vous faites lorsque vous écrivez « N_ x _ = » (Avec N = 2xA) dans la partie inférieure à droite lors de l'étape 4. Et lors de l'étape 5, vous cherchez le plus grand entier B qui peut remplacer les signes « _ » tel que (2×10A + B) × B ≤ N1.
10
Soustrayez la surface (2×10A + B) × B à la surface totale (à gauche, comme dans l'étape 6), ce qui vous donne la surface : S-(10A+B)² qui n'est pas encore prise en compte (et qui sera utilisée pour calculer le chiffre suivant en utilisant la même méthode qu'au-dessus).
11
Pour obtenir le troisième chiffre, répétez la manœuvre. Abaissez la paire suivante (S_c) depuis S pour obtenir N2 à gauche Cherchez le plus grand entier C qui satisfasse la condition suivante : (2×10×(10A+B)+C) × C ≤ N2 (ce qui équivaut à écrire deux fois le nombre à deux chiffres « A B » suivi de « _ x _ = » et à trouver le plus grand entier qui peut remplacer les signes « _ »).

Publicité

Conseils

Déplacer la virgule de deux places dans un nombre décimal (multiplication par 100 ou par 0,01 suivant le cas) revient à déplacer la virgule d'une place pour la racine carrée de ce nombre (multiplication par 10 ou par 0,1 suivant le cas).
Cette méthode fonctionne pour toutes les bases de calcul, pas seulement en base 10 (décimale).
Dans cet exemple, 1,73 peut être vu comme un « reste », car : 780,14 = 27,9² + 1,73.
N'hésitez pas à présenter les calculs de la façon qui vous convient le mieux ! Certaines personnes écrivent, par exemple, le résultat au-dessus du nombre de départ.
Il existe une autre méthode utilisant les fractions continues et elle s'appuie sur la formule suivante : √z = √(x²+y) = x + y/(2x + y/(2x + y/(2x + ...))). Par exemple, pour calculer la racine carrée de 780,14, la racine du carré le plus proche de 780,14 est 28. On a donc : z = 780,14, x = 28 et y = -3,86. On fait l'application numérique. Si on prend juste x + y/(2x), on obtient 78207/2800, c'est-à-dire environ 27,931(1) ; avec le nouveau terme, ça donne 4374188/156607, soit environ 27,930986(5). Chaque terme ajoute environ 3 chiffres de précision par rapport au terme précédent.

Avertissement

Assurez-vous de bien séparer les chiffres par paires en partant de la virgule. Si vous séparez 79 520 789 182,47897 en « 79 52 07 89 18 2,4 78 97 », le résultat obtenu ne sera pas le bon.