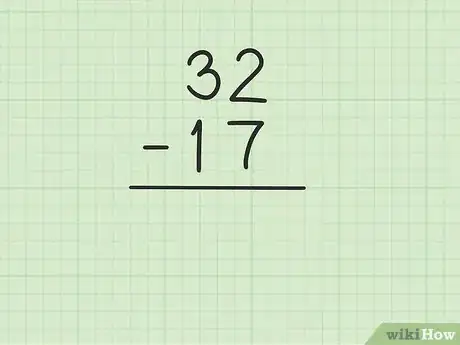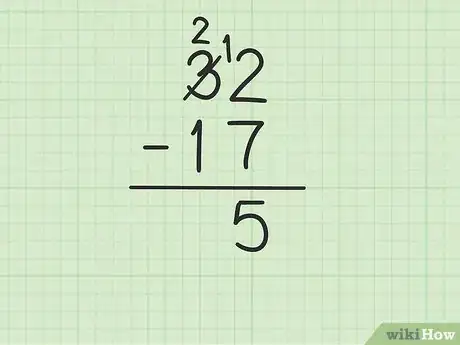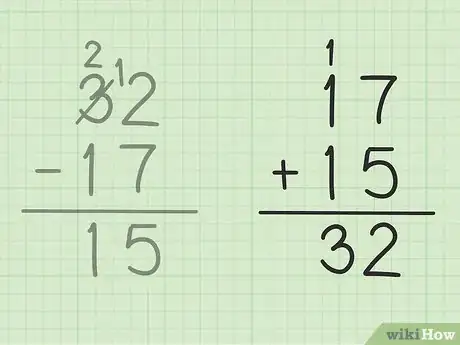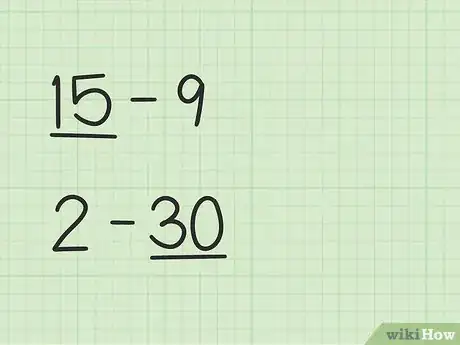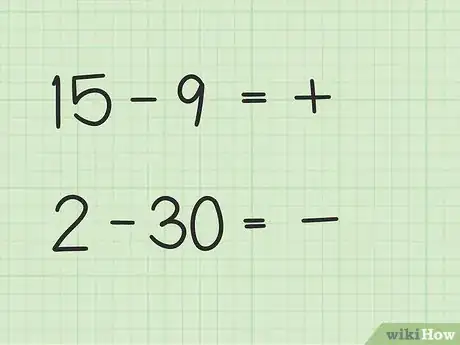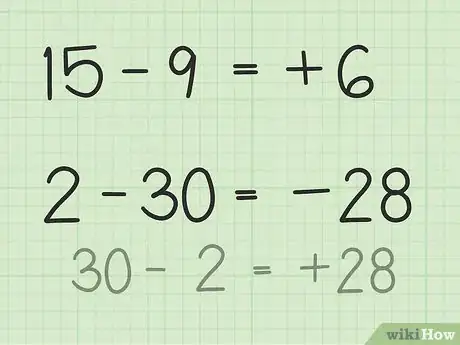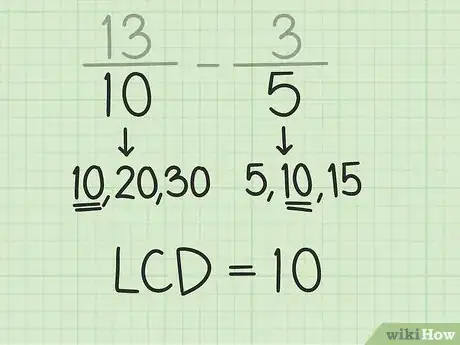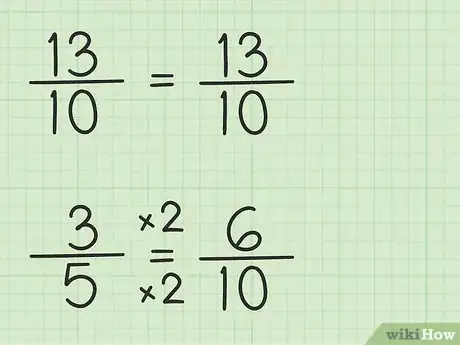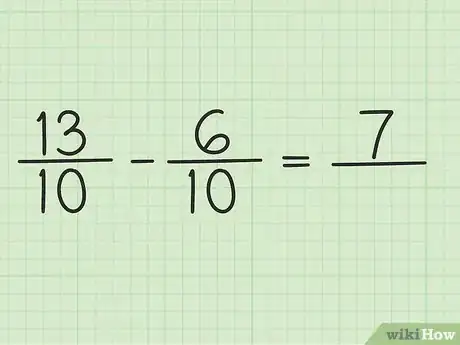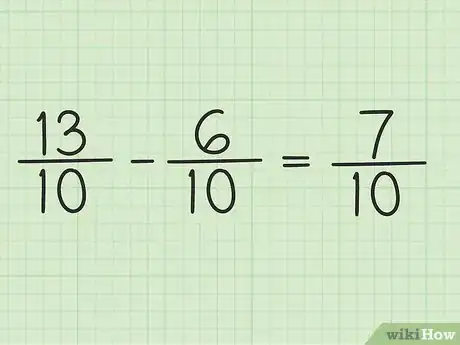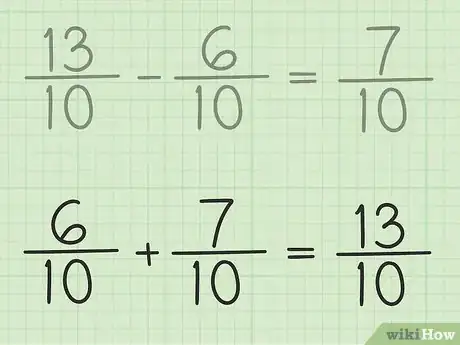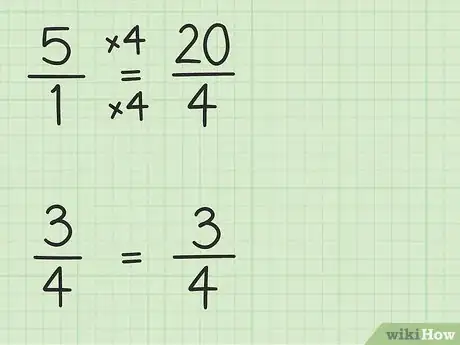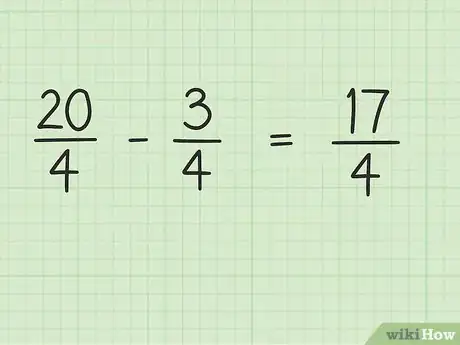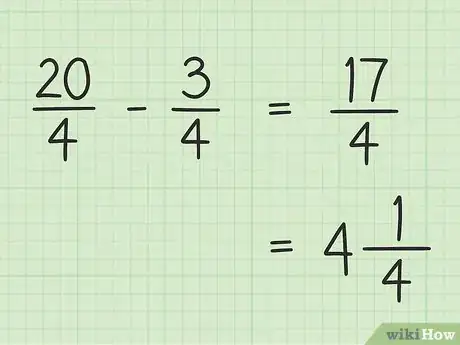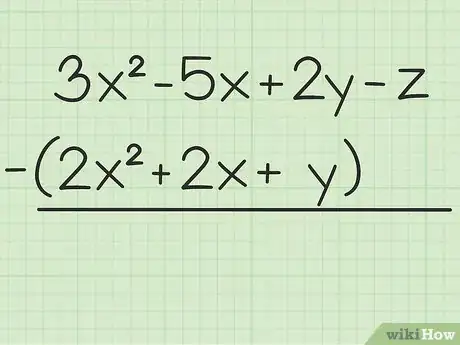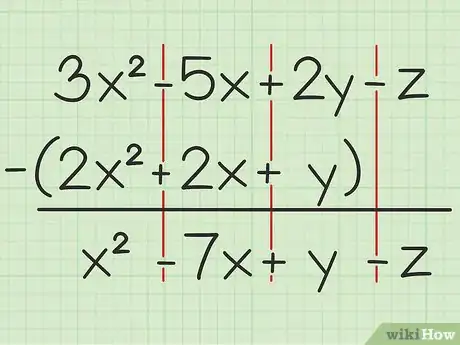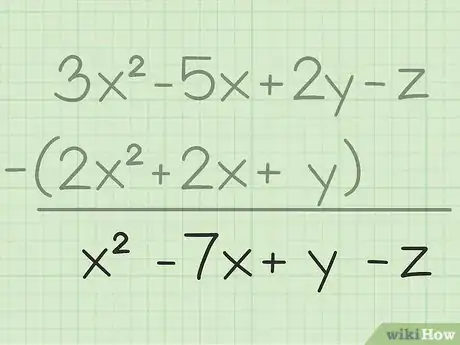Comment faire une soustraction

Informations concernant l'auteur.e

La soustraction est une opération mathématique qui consiste à retirer un nombre d'un autre. Si la soustraction de deux nombres entiers est assez simple, elle devient un peu plus difficile avec des valeurs plus complexes, comme des fractions ou des nombres décimaux. Cependant, une fois le principe assimilé, vous pourrez effectuer tout type de soustraction et vous pourrez aborder d'autres opérations comme l'addition, la multiplication ou encore la division. Voyons tout de suite les différents types de soustraction.

Méthode 1

Méthode 1 sur 6:
Soustraire de grands entiers en utilisant la retenue

1
Commencez par noter le plus grand nombre. Admettons que vous ayez à résoudre la soustraction suivante : 32 - 17. Inscrivez 32 en premier.
2
Inscrivez le plus petit nombre juste en dessous. Les chiffres doivent être alignés verticalement : les dizaines sous les dizaines, idem pour les unités. Ainsi, dans notre exemple, le « 1 » de 17 sera juste sous le « 3 » du 32 et le « 7 » de 17 sera sous le « 2 » de 32.
3
Commencez la soustraction par la colonne des unités. Il convient donc de retirer le chiffre du bas du chiffre du haut. Cette opération ne pose pas de problème particulier, sauf si le chiffre du bas est supérieur à celui du haut, ce qui est le cas dans notre exemple (7 > 2). En ce cas, voici comment on procède :
- « empruntez » une dizaine au 3 de 32 afin d'avoir, non pas 2, mais 12,
- barrez le 3 de 32 et mettez un petit 2 à la place, puis mettez un petit 1 à gauche du 2 des unités pour avoir 12,
- désormais, votre soustraction se présente ainsi : 12 - 7, soit 5. Inscrivez ce chiffre 5 sous le trait de soustraction, à l'aplomb de ces deux chiffres.
4
Passez à la colonne des dizaines et soustrayez de la même façon, à savoir le chiffre du haut moins le chiffre du bas. Souvenez-vous que le 3 de 32 s'est transformé en un 2 (après emprunt d'une dizaine). Côté dizaine, vous devez donc soustraire 1 à 2, soit 2 - 1 = 1. Inscrivez ce résultat sous le trait d'opération, dans la colonne des dizaines, à gauche du 5 des unités. Vous lisez alors 15. C'est votre réponse : 32 - 17 = 15.
5
Vérifiez vos calculs. Afin de vérifier la justesse de vos calculs, il suffit, par exemple, de prendre le résultat final et de lui ajouter le plus petit des deux nombres de la soustraction. Vous devez retomber sur le plus grand. Dans notre exemple, si on ajoute 15 (le résultat) à 17 (le plus petit des deux nombres), on obtient 32 (15 + 17 = 32). C'est bien le plus grand des deux nombres et l'opération est donc juste !

Publicité

Méthode 2

Méthode 2 sur 6:
Soustraire de petits nombres

1
Repérez dans la soustraction quel est le plus grand des deux nombres. L'opération 15 - 9 est très différente de l'opération 2 - 30.
- Avec 15 - 9, le premier nombre, 15, est plus grand que le second, 9.
- Avec 2 - 30, le second nombre, 30, est plus grand que le premier, 2.
2
Déterminez à l'avance si la réponse sera positive ou négative. Si le premier nombre est supérieur au second, elle sera positive, dans le cas contraire, elle sera négative.
- Pour 15 - 9, la réponse sera positive, car le premier nombre est supérieur au second.
- Pour 2 - 30, la réponse sera négative, car le second nombre est supérieur au premier.
3
Trouvez l'écart existant entre les deux nombres. Pour pouvoir soustraire deux nombres, on peut essayer de visualiser mentalement l'écart existant entre eux afin de compter les unités.
- Pour 15 - 9, imaginez une pile de 15 jetons de poker. Retirez-en 9 : il vous en restera 6, donc 15 - 9 = 6. Vous pouvez aussi imaginer une ligne numérotée. Pensez à une ligne qui irait de 1 à 15, revenez en arrière de 9 unités, vous êtes sur le nombre 6. Le résultat est identique. Heureusement !
- Pour 2 - 30, le plus simple consiste à inverser les deux nombres, puis à faire l'opération et enfin, à inverser le signe. Ainsi, 30 - 2 = 28, car 28 n'est qu'à deux unités de 30. Il faut à présent inverser le signe qui devient alors négatif. Vous avez au préalable repéré que le second nombre était supérieur au premier, donc la réponse est forcément négative. Au final, 2 - 30 = - 28.
Publicité

Méthode 3

Méthode 3 sur 6:
Soustraire des nombres décimaux

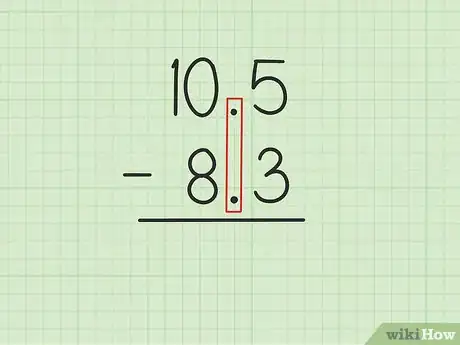
1
Inscrivez le plus grand de deux nombres au-dessus du plus petit, en alignant verticalement les virgules. Admettons que vous ayez à résoudre la soustraction suivante : 10,5 - 8,3. Inscrivez 8,3 au-dessous de 10,5 et faites correspondre les virgules. Alignez les autres chiffres (dizaines ensemble…). Le « , 5 » de 10,5 sera aligné avec le « , 3 » de 8,3 et le 0 est aligné avec le 8.
- Si, après la virgule, les deux nombres n'ont pas le même nombre de décimales, ne paniquez pas ! Il suffit de combler les décimales manquantes par des zéros. Au final, vous devez avoir le même nombre de décimales pour les deux nombres. Prenons l'exemple suivant : 5,32 - 4,2. Il manque une décimale à ce dernier chiffre, on met un 0. L'opération devient alors : 5,32 - 4,20. Ce faisant, vous n'avez pas changé la valeur du second chiffre et vous allez pouvoir faire tranquillement votre opération.
2
Commencez la soustraction par la dernière colonne des décimales, ici les dixièmes. Comme cela a été fait précédemment, il convient de retirer le chiffre du bas du chiffre du haut. C'est en tout point identique à une soustraction d'entiers, il faut juste bien poser l'opération au départ en alignant les virgules. Dans notre exemple, on commence par retirer 3 à 5, soit 5 - 3 = 2. Ce résultat, vous l'inscrirez sous le trait d'opération, à l'aplomb du 3 de 8,3.
- Avant de passer à la colonne juste à gauche, il convient d'abaisser la virgule. Votre réponse est pour lors : , 2.
3
Poursuivez la soustraction avec la colonne des unités. Comme toujours, il convient de retirer le chiffre du bas du chiffre du haut. Ici, il faut soustraire 8 de 0. Empruntez une dizaine dans la colonne des dizaines et comme il n'y en a qu'une, vous barrez le 1 et vous mettez un 1 à la place, ce qui vous fait 10 dans les unités. Vous pouvez alors soustraire 8 de 10, soit 10 - 8 = 2. Vous aurez remarqué que le 10 était déjà en place et on aurait donc pu s'épargner cette étape. Inscrivez votre résultat (2) juste en dessous du 8, à gauche de la virgule.
4
Donnez votre réponse définitive : 10,5 - 8,3 = 2,2. La réponse est donc : 2,2.
5
Vérifiez vos calculs. Afin de vérifier la justesse de vos calculs, il suffit, par exemple, de prendre le résultat final et de lui ajouter le plus petit des deux nombres de la soustraction. Vous devez retomber sur le plus grand. Dans notre exemple, si on ajoute 2,2 et 8,3, on obtient 10,5. Le compte est bon !

Publicité

Méthode 4

Méthode 4 sur 6:
Soustraire des fractions

1
Alignez horizontalement les dénominateurs et les numérateurs des deux fractions. Admettons que vous ayez à résoudre la soustraction suivante : 13/10 - 3/5. Les deux numérateurs, 13 et 3, doivent être sur la même ligne. Idem pour les deux dénominateurs, 10 et 5. Entre les deux fractions se trouve le signe « - ». Ainsi présenté, vous visualiserez mieux le problème.
2
Trouvez le plus petit commun multiple (PPCM) des dénominateurs. Le plus petit commun multiple des deux nombres est la plus petite valeur divisible par ces deux nombres. Dans notre exemple, il faut trouver le PPCM de 10 et de 5. C'est en fait 10, car ce nombre est divisible par 10 et par 5. Il n'y en a pas de plus petit.
- Notez au passage que le PPCM n'est pas forcément un des deux nombres. Ainsi, le PPCM de 3 et 2 est 6. Il n'y en a pas de plus petit.
3
Récrivez les fractions en les réduisant au même dénominateur. La fraction 13/10 ne bouge pas, car elle est déjà sur 10. Par contre, la seconde fraction, 3/5, doit être ramenée sur 10. Dans 10, il y a 2 fois 5. La fraction 3/5 doit donc être multipliée par 2/2 afin d'obtenir un dénominateur égal à 10. On a donc : 3/5 x 2/2 = 6/10. Cette dernière fraction est une fraction dite « équivalente » à la fraction de départ (3/5 = 6/10). Désormais, les deux fractions sont sur 10, on peut donc les soustraire.
- L'opération se présente alors ainsi : 13/10 - 6/10.
4
Soustrayez les deux numérateurs. Faites simplement la soustraction : 13 - 6 = 7. Les dénominateurs, quant à eux, restent inchangés.
5
Inscrivez le nouveau numérateur sur le dénominateur commun et vous aurez votre réponse définitive. On a vu que le nouveau numérateur était 7. Les deux fractions ont le même dénominateur, 10. En conclusion, la réponse finale est : 7/10.
6
Vérifiez vos calculs. Afin de vérifier la justesse de vos calculs, il suffit, par exemple, de prendre la fraction finale et de lui ajouter la plus petite des fractions. Vous devriez retomber sur l'autre fraction. Ici, vous devez faire : 7/10 + 6/10 = 13/10. Le compte est bon !

Publicité

Méthode 5

Méthode 5 sur 6:
Soustraire une fraction d'un nombre entier

1
Posez bien le problème. Admettons que vous ayez à résoudre la soustraction suivante : 5 - 3/4. Inscrivez l'opération sur votre feuille.
2
Transformez le nombre entier en une fraction dont le dénominateur est identique à celui de la fraction. Ici, vous devez transformer le chiffre 5 en une fraction dont 4 sera le dénominateur. Ainsi, vous pourrez faire la soustraction, les deux fractions étant réduites au même dénominateur. On commence par transformer 5 en une fraction élémentaire : 5 = 5/1. Puis, on multiplie numérateur et dénominateur par 4 pour obtenir une fraction équivalente : 5/1 x 4/4 = 20/4. Vous pouvez faire le calcul, cette dernière fraction est bien égale à 5. On peut maintenant faire la soustraction.
3
Récrivez l'opération. Elle se présente ainsi : 20/4 - 3/4.
4
Comme précédemment, soustrayez les deux numérateurs et conservez le dénominateur. On enlève donc 3 de 20, ce qui donne 17 (20 - 3 = 17). C'est le nouveau numérateur. Le dénominateur reste 4.
5
Notez votre réponse définitive. La réponse est : 17/4. C'est une fraction dite « impropre ». Si vous voulez la présenter sous la forme d'un nombre mixte (entier et fractionnaire), divisez simplement 17 par 4, ce qui donne 4 et il vous reste 1. La réponse est : 4 1/4.

Publicité

Méthode 6

Méthode 6 sur 6:
Soustraire des inconnues

1
Posez bien le problème. Admettons que vous ayez à résoudre la soustraction suivante : (3x² - 5x + 2y - z) - (2x² + 2x + y). Inscrivez la seconde somme sous la première.
2
Soustrayez les termes identiques. Quand des inconnues sont en jeu, on ne peut les soustraire qu'aux deux conditions qu'elles soient identiques (x, y ou z) et élevées à la même puissance. Pour prendre un exemple concret, on peut retirer 4x² de 7x², mais non 4x de 4y. Partant de ces principes, vous pouvez décomposer l'opération terme à terme :
- 3x² - 2x² = x²
- - 5x - 2x = - 7x
- 2y - y = y
- - z - 0 = - z
3
Notez votre réponse définitive. Vous avez soustrait terme à terme tous les éléments de l'opération. Vous pouvez donner la réponse finale qui est la suivante :
- 3x² - 5x + 2y - z - (2x² + 2x + y) = x² - 7x + y - z
Publicité

Conseils

Quand on a affaire à un grand nombre, il est possible de soustraire par étapes. Prenons l'exemple concret suivant : 63 jetons - 25 jetons. Vous n'êtes pas obligé d'enlever les 25 d'un coup. Vous pouvez commencer par en enlever 3 : il vous en reste 60. Si vous enlevez encore 20, il vous en reste 40. Enfin, si vous en enlevez encore 2, il vous en restera 38. Vous n'avez pas eu besoin d'en passer par un emprunt aux dizaines.

Avertissements

Si vous avez à soustraire des nombres positifs et négatifs, les choses deviennent beaucoup plus compliquées. En ce cas, lisez cet article de wikiHow intitulé : Comment additionner et soustraire des nombres entiers.