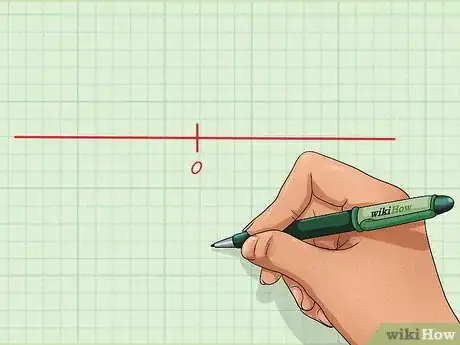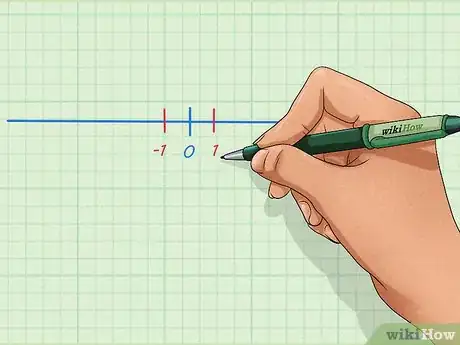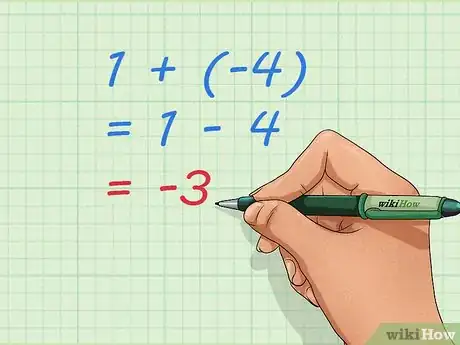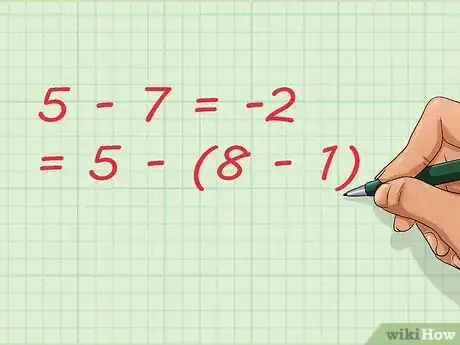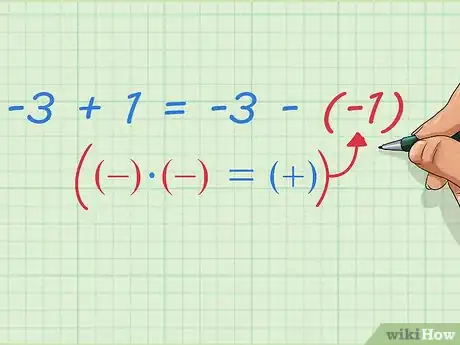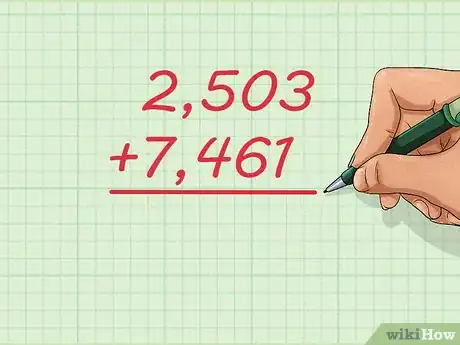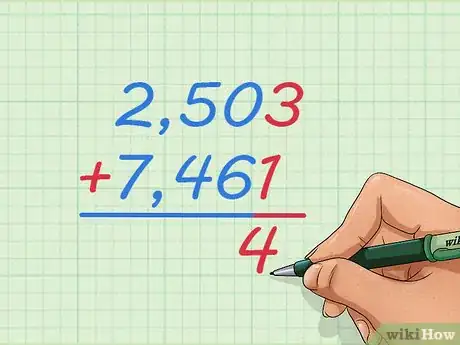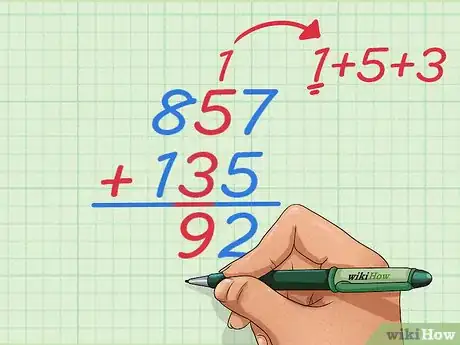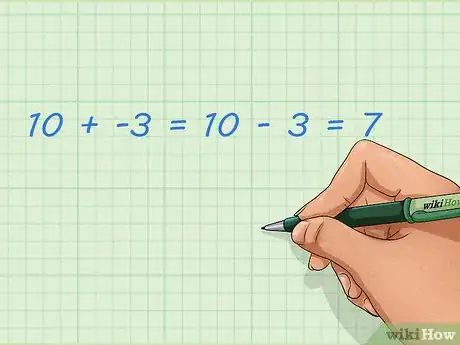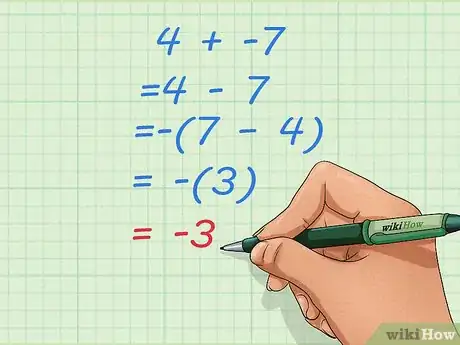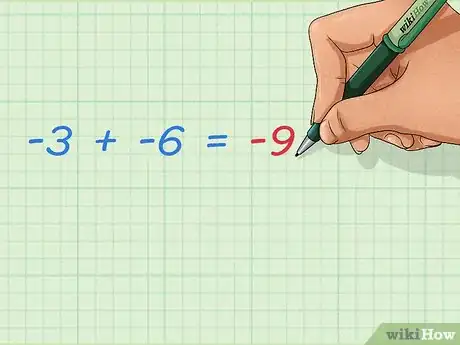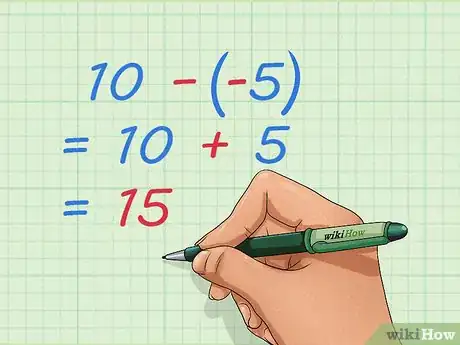Comment additionner et soustraire des nombres entiers

Un nombre entier est un nombre qui n'a pas de partie décimale ou une partie décimale nulle. S'il appartient à un groupe d'entiers positifs (> 0) et négatifs (< 0), ces entiers sont dits relatifs, si le groupe n'est composé que d'entiers positifs, ils sont dits naturels. Le groupe 3, -12, 17, 0, 7 000 et -582 est composé d'entiers relatifs. En fait, dans l'ensemble des entiers relatifs, vous avez tous les entiers naturels et tous leurs opposés, 0 est à part, car il est son propre opposé [1] . Cette différence entre entiers naturels et relatifs peut sembler compliquée, mais il n'en est rien, la terminologie n'est destinée qu'à ceux qui font des recherches compliquées. Ce que vous devez retenir, c'est qu'un entier est toute valeur numérique sans décimale et qui ne se présente pas sous forme fractionnaire.

Méthode 1
Méthode 1 sur 5:
Additionner et soustraire des entiers sur une droite graduée

  1. Image intitulée Add and Subtract Integers Step 1
    1
    Comprenez l'intérêt d'une ligne graduée. Cela peut sembler bizarre, mais une simple ligne graduée régulièrement sur une feuille de papier peut vous permettre de mieux comprendre ce qu'est la somme et la différence d'entiers. Nul besoin d'une calculatrice, un trait horizontal gradué et vous allez tout comprendre rapidement [2]  !
  2. Image intitulée Add and Subtract Integers Step 2
    2
    Tracez une ligne graduée et éventuellement orientée. Commencez par une ligne horizontale que vous allez séparer en deux parties par un petit trait vertical qui sera noté 0.
    • Dans les livres d'école, ce point 0 est aussi appelé « point origine », puisque c'est à partir de lui que l'on compte dans un sens, à droite, comme dans l'autre, à gauche.
  3. Image intitulée Add and Subtract Integers Step 3
    3
    Tracez ensuite deux autres petits traits verticaux. Ils seront de part et d'autre du 0 et à égale distance. Celui de droite sera noté 1, tandis que celui de gauche représentera -1. Ces deux entiers sont les plus proches de 0.
    • La précision des espaces entre deux tirets n'est pas primordiale, puisque le but est de comprendre comment on peut compter sur cette ligne.
    • La gauche et la droite se définissent quand l'on est face à la ligne, 0 étant le repère primordial.
  4. Image intitulée Add and Subtract Integers Step 4
    4
    Remplissez votre ligne. Sur le même principe que le 1 et le -1, mettez d'autres entiers. Ainsi, vous mettrez à droite, avec des petits tirets et dans cet ordre, 2, 3 et 4, et ferez de même à gauche, mais cette fois-ci, en allant vers la gauche, vous mettrez -2, -3 et -4. Mettez autant de repères que cela est nécessaire.
    • Sur l'illustration, nous avons décidé d'avoir une ligne qui va de -6 à 6.
  5. Image intitulée Add and Subtract Integers Step 5
    5
    Comprenez bien ce que sont les entiers positifs et les entiers négatifs. Un entier positif est aussi appelé « entier naturel [3]  ». Tout entier strictement supérieur à 0, comme 1, 2, 3, 25, 99 ou 2 007, est un entier naturel. À l'opposé, tout entier négatif est strictement inférieur à 0, c'est le cas de -2, -4 ou -88.
    • Un entier porte bien son nom, il est… entier. Il n'est pas divisé, comme 1/2 qui est une fraction, il n'est pas non plus affligé d'une virgule qui viendrait lui ajouter un petit quelque chose, comme 1,25. En somme, ce n'est ni une fraction ni une valeur décimale… c'est un entier !
  6. Image intitulée Add and Subtract Integers Step 6
    6
    Commencez la somme. Supposons que vous ayez à calculer 1 + 2. À l'aide de la ligne graduée, vous allez visualiser l'opération. Pointez votre doigt sur le 1, puisque l'addition commence par ce chiffre, mais comme l'addition est commutative (elle peut se faire dans les deux sens), vous auriez aussi bien pu commencer par 2.
    • Trouvez-vous cela trop simple ? Oui, bien sûr… si vous savez déjà faire une addition ! Vous direz avec raison qu'il n'y a pas besoin d'utiliser une ligne graduée pour un calcul aussi simple. Mais ce ne sera pas toujours le cas. Cet exemple n'est là que pour bien comprendre le mécanisme de l'addition des entiers.
  7. Image intitulée Add and Subtract Integers Step 7
    7
    Ajoutez 2. L'opération vous signifie d'ajouter 2 (+ 2). Déplacez votre doigt de deux espaces, dans le sens positif, vers la droite. Une fois arrivé en face du trait, arrêtez-vous. Là, vous lisez 3 : c'est la réponse de l'opération.
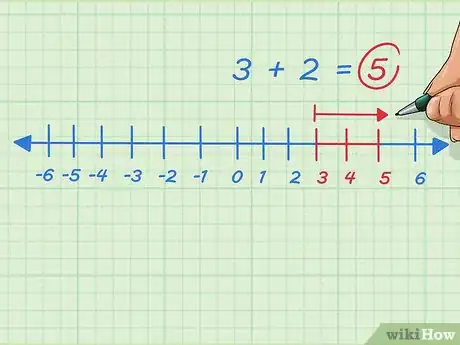
  8. Image intitulée Add and Subtract Integers Step 8
    8
    Ajoutez tout entier positif en allant vers la droite de la ligne graduée. Vous avez à faire la somme 3 + 2. Vous pointez vers le 3, puis vous glissez votre doigt de 2 crans vers la droite et vous lisez 5 : 3 + 2 = 5.
  9. Image intitulée Add and Subtract Integers Step 9
    9
    Soustrayez en allant vers la gauche de la ligne graduée. Cherchez le résultat de 6 - 4, pointez le doigt sur le 6, puis reculez-le de 4 crans et vous lisez 2 : 6 - 4 = 2.
    Publicité

Méthode 2
Méthode 2 sur 5:
Additionner et soustraire des entiers négatifs (droite graduée)

  1. Image intitulée Add and Subtract Integers Step 10
    1
    Sachez ce qu'est une ligne graduée. Pour savoir ce qu'est une telle ligne graduée qui permet de faire des opérations sur les entiers, reportez-vous à la 1re étape de la 1re méthode (ci-dessus).
  2. Image intitulée Add and Subtract Integers Step 11
    2
    Comprenez bien ce qu'est un nombre négatif [4] . Additionner un nombre positif sur une ligne graduée, c'est se déplacer vers la droite de cette ligne, tandis qu'additionner un nombre négatif sur cette même ligne, c'est se déplacer vers la gauche de cette ligne.
    • Ainsi, supposons que vous ayez à additionner 1 et -4. Le signe « - » peut être trompeur, car c'est à la fois le signe opératoire, mais aussi celui de la distance, négative, du nombre par rapport à 0. L'opération s'écrit simplement ainsi :
      1 + (-4)

      Sur votre ligne graduée, vous allez commencer à 1 et vous vous déplacerez de 4 crans vers la gauche, ce qui vous donnera comme résultat -3.
  3. Image intitulée Add and Subtract Integers Step 12
    3
    Sachez transformer l'égalité d'une somme avec un nombre négatif. La réponse - 3 est celle que l'on obtient en faisant : 1 - 4. Or, c'est aussi la réponse de : 1 + (-4). La réponse étant la même pour les opérations avec les mêmes facteurs, vous pouvez poser l'égalité suivante :

    1 + (-4) = 1 - 4 = -3
  4. Image intitulée Add and Subtract Integers Step 13
    4
    Pensez toujours à transformer une somme contenant un nombre négatif. En effet, une telle somme peut se convertir en une soustraction. Pour faire plus simple, ajouter un nombre négatif à un autre nombre revient à soustraire le premier du second. Mathématiquement, la somme x + (-y) est strictement équivalent à x- y.
    • Ainsi, -4 est un entier relatif négatif. L'additionner à un nombre positif, 1 par exemple, revient à diminuer ce dernier de 4 unités, ce qui, en mathématiques, on l'a vu précédemment, revient à écrire l'égalité suivante :

      1 + (-4) = 1 - 4


      Sinon, vous pouvez tenir le raisonnement suivant en gardant le principe de l'addition : à partir de 1, vous ajoutez 4 unités vers la gauche, ce qui revient à ajouter -4. Que vous preniez l'une ou l'autre des formulations, vous retombez toujours sur l'égalité :

      1 - 4 = 1 + (-4)
  5. Image intitulée Add and Subtract Integers Step 14
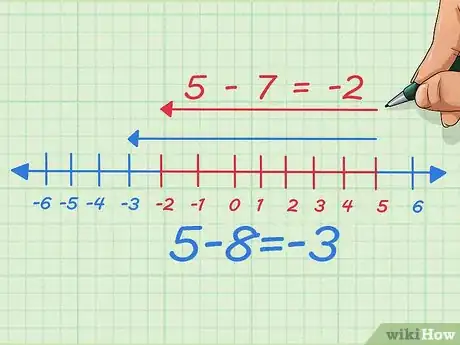
    5
    Comprenez bien le lien entre soustraction et nombres négatifs. Sur une ligne graduée, le fait de déplacer son doigt vers la gauche peut signifier à la fois la soustraction d'un entier positif tout comme l'addition d'un entier négatif [5] . Faisons l'opération suivante : 5 - 8.
    • Sur la ligne graduée, vous repérez le 5, vous vous déplacez de 8 crans vers la gauche et vous lisez -3.
  6. Image intitulée Add and Subtract Integers Step 15
    6
    Modifiez la quantité à soustraire et voyez ce que cela donne. Supposons que vous ne diminuiez plus du montant indiqué par l'opération, mais par ce montant diminué d'une unité, ici une diminution de 7 unités au lieu de 8. En allant toujours sur la gauche, vous vous arrêterez une unité avant. Concrètement, vous devez trouver le résultat de

    5 - 8 = -3


    Mais vous décidez de voir ce que donne la soustraction légèrement différente :

    5 - 7 = -2
  7. Image intitulée Add and Subtract Integers Step 16
    7
    Comprenez que la soustraction d’un entier négatif est une addition. Dans l’exemple précédent, nous avons décidé de soustraire non pas 8, mais 7, c’est-à-dire : 8 -1. Mathématiquement, l’égalité suivante, même si elle parait bizarre, mais c’est pour les besoins de la cause, est vraie :
    5 - 7 = 5 - (8 - 1) = -2
  8. Image intitulée Add and Subtract Integers Step 17
    8
    Sachez changer un signe « - » en signe « + ». Selon notre exemple, mais surtout selon une certaine loi d’algèbre, soustraire à une valeur une valeur négative revient à ajouter cette dernière à la première :
    5 - 7 = 5 - (8 - 1) = = 5 - 8 + 1
    • Nous savons déjà que 5 - 8 = -3, il ne reste donc plus qu’à remplacer cette somme par sa valeur (-3), ce qui donne :
      5 - (8 - 1) = 5 - 7 = -3 + 1
    • Nous savons où se trouve, sur une ligne graduée, 5 - (8 - 1), c’est-à-dire à un espace plus vers la droite que 5 - 8. Cela revient à dire que - 2 est à droite de - 3. Mathématiquement, cela peut s’écrire ainsi :

      -3 - (-1) = -3 + 1
  9. Image intitulée Add and Subtract Integers Step 18
    9
    Transformez les soustractions de nombres négatifs en addition. À l’appui de l’exemple précédent, nous avons vu que :

    -3 + 1 = -3 - (-1)


    De façon plus théorique, nous pouvons écrire que :

    nombre a - nombre b négatif = nombre a + nombre b positif.

    En cours, votre professeur(e) vous rappellera cette règle de façon raccourcie en vous disant que :

    pour l’addition, deux moins donne un plus.
    .
    Publicité

Méthode 3
Méthode 3 sur 5:
Additionner de grands entiers positifs

  1. Image intitulée Add and Subtract Integers Step 19
    1
    Trouvez le résultat de l'addition suivante : 2 503 + 7 461. Posez l'opération en alignant verticalement les chiffres depuis la droite. Une fois la chose faite, le 2 de 2 503 sera au-dessus du 7 de 7 461, le 5 au-dessus du 4, etc. Dans cette partie, nous allons étudier des sommes qui ne peuvent être effectuées facilement de tête ou sur une ligne graduée.
    • Mettez un « + » à gauche du nombre du bas et n'oubliez pas de mettre un trait d'opération au bas des deux nombres, comme c'était déjà le cas avec les petites additions.
  2. Image intitulée Add and Subtract Integers Step 20
    2
    Commencez par faire la somme des deux chiffres de droite. Il peut sembler bizarre de commencer par la droite, car la lecture de ces mêmes nombres se fait de gauche à droite, mais c'est à cause des retenues éventuelles. C'est une procédure facile à retenir cependant [6]  !
    • À l'aplomb des deux nombres à droite, 3 et 1, et sous le trait de sommation, inscrivez le résultat de 3 + 1, soit 4.
  3. Image intitulée Add and Subtract Integers Step 21
    3
    Continuez l'addition. Procédez de la même façon en vous déplaçant chaque fois d'un rang vers la gauche. Vous allez additionner 0 + 6, 5 + 4 et 2 + 7. Les réponses sont toujours inscrites à l'aplomb de l'opération.
    • Vous devriez trouver, comme réponse à l'addition proposée, 9 964. Vérifiez tous vos calculs si vous n'arrivez pas à ce résultat.
  4. Image intitulée Add and Subtract Integers Step 22
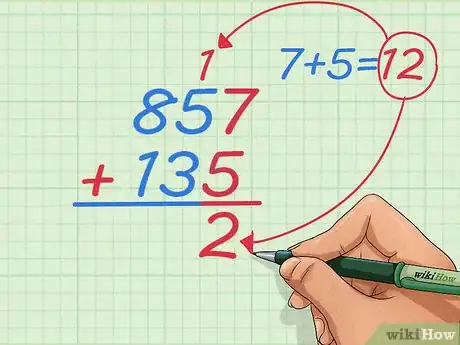
    4
    Faites la somme de 857 et de 135 (857 + 135). La somme se fait comme précédemment, sauf que dans ce cas, dès la première addition (7 + 5), vous obtenez un nombre à deux chiffres, à savoir 12. Or, il ne faut poser qu'un seul chiffre sous le trait de sommation. En ce cas, il faut procéder d'une certaine façon que l'on va voir et c'est à cause de cette particularité que l'addition commence toujours à droite.
  5. Image intitulée Add and Subtract Integers Step 23
    5
    Faites normalement la somme de 7 et de 5. Vous obtenez donc 12. Dans ce cas, il faut poser sous le trait l'unité, et ici ce sera le 2, tandis que le 1 des dizaines est mis en retenue et inscrit, en petit, au-dessus de la colonne de chiffres suivant, soit au-dessus du 5 de 857.
    • Pour comprendre ce qu'il se passe, il suffit de penser au fait que sous les unités, il ne peut y avoir que des unités et aussi au fait que 12 = 10 + 2. La dizaine récupérée est donc mise dans la colonne suivante… celle des dizaines, d'où le petit 1 de retenue.
  6. Image intitulée Add and Subtract Integers Step 24
    6
    Additionnez la deuxième colonne. Additionnez 5+3, sans oublier d’ajouter la retenue de l’addition précédente (1). C’est ainsi que 9 (5 + 3 + 1) est le chiffre du milieu de votre résultat. Pour l’instant, la réponse se termine par 92.
  7. Image intitulée Add and Subtract Integers Step 25
    7
    Additionnez la troisième et dernière colonne. Vous avez compris le principe, vous devez additionner les colonnes de la droite vers la gauche jusqu’à épuisement des colonnes. Dans notre cas, il ne reste plus qu’à ajouter 8 et 1, soit 9. La réponse est la suivante : 857 + 135 = 992.
    • Maintenant, vous pouvez faire des additions plus compliquées avec, par exemple, des retenues systématiques, comme en additionnant 974 et 568. Quand vous additionnez une colonne et que vous trouvez un nombre à deux chiffres, vous posez comme résultat l’unité du résultat et vous mettez en retenue au-dessus de la colonne suivante la dizaine du résultat. Si la somme de la dernière colonne donne un nombre à deux chiffres, vous l’inscrivez tel quel.
    • Pour vérifier la bonne réponse de la somme 974 + 568, allez jeter un coup d'œil à la section Conseils.
    Publicité

Méthode 4
Méthode 4 sur 5:
Soustraire de grands entiers

  1. Image intitulée Add and Subtract Integers Step 26
    1
    Posez bien l'opération. Si vous devez calculer 4 713 - 502, mettez le second nombre sous le premier en alignant verticalement les chiffres de la droite vers la gauche. Le 2 sera sous le 3, le 0 sous le 1, le 5 sous le 7 et le 4 sera tout seul en haut.
    • Au début, vous pouvez parfaitement mettre un 0 sous le 4 si cela vous aide d'une quelconque façon. Mettre un ou plusieurs 0 à gauche d'un nombre ne modifie en rien sa valeur, c'est juste un arrangement qui peut s'avérer pratique. Par contre, un 0 à droite d'un nombre le modifie radicalement.
  2. Image intitulée Add and Subtract Integers Step 27
    2
    Opérez comme il faut. Commencez toujours à droite en soustrayant le chiffre du bas de celui du haut, faites de même en progressant vers la gauche [7] . Faites 3 - 2, puis 1 - 0, 7 - 5 et enfin 4 - 0, en inscrivant chaque réponse sous le trait de sommation et à l'aplomb de l'opération.
    • Si vous ne vous êtes pas trompé.e, vous allez trouver 4 211.
  3. Image intitulée Add and Subtract Integers Step 28
    3
    Résolvez de la même façon la soustraction 924 - 518. Ces nombres ayant le même nombre de chiffres, l'alignement sera parfait. Là n'est pas le problème : cette soustraction pose un nouveau problème si vous n'avez jamais fait ce type d'opération.
  4. Image intitulée Add and Subtract Integers Step 29
    4
    Commencez à droite. Comme précédemment, vous devez commencer par soustraire les deux chiffres de droite et ici vous devez faire 4 - 8. Si vous avez lu ce qui précédait, vous savez que 4 - 8 = -4, mais dans une opération posée, il ne peut y avoir de chiffres négatifs, il faut donc procéder différemment.
    • Il faut emprunter 1 (une dizaine) au chiffre des dizaines (ici, 2) du nombre du haut. Le 2 est donc barré et remplacé au-dessus par 1 (2 - 1).
    • Le 4 des unités de 924 récupère la dizaine empruntée à gauche et devient 14 (4 + 10). Pour cela, inscrivez un petit 1 juste à gauche du 4, ce qui fait que maintenant, vous avez une soustraction faisable, puisqu'il s'agit de
      14 - 8.
    • Ce qui a été fait s'explique logiquement. 924 peut s'écrire de différentes façons : 924 = 900 + 20 + 4 = 900 + 10 + 10 + 4 = 910 + 14. C'est la raison pour laquelle vous avez barré le 2 pour le remplacer par un 1 et ajouté un 1 au 4 des unités.
  5. Image intitulée Add and Subtract Integers Step 30
    5
    Faites l'opération 14 - 8. Comme d'habitude, inscrivez le résultat sous le trait d'opération et à l'aplomb de l'opération. Ici, il faut inscrire 6 : ce sera l'unité de la réponse.
  6. Image intitulée Add and Subtract Integers Step 31
    6
    Passez à la colonne suivante. Attention ! Le 2 s'est transformé en 1 avec l'emprunt, vous devez donc faire : 1 - 1, ce qui donne 0.
    • La réponse se termine pour l'instant par 06.
  7. Image intitulée Add and Subtract Integers Step 32
    7
    Passez à la dernière colonne. Ici, pas d'emprunt, de retenue, juste une soustraction toute simple, à savoir 9 - 5, soit 4. La réponse est donc la suivante : 924 - 518 = 406.
  8. Image intitulée Add and Subtract Integers Step 33
    8
    Entrainez-vous à soustraire un grand nombre d'un nombre inférieur. Supposons que vous ayez à faire l'opération suivante : 415 990 - 968 772. En posant l'opération, vous vous apercevez vite qu'il y a quelque chose d'original : le nombre du bas est supérieur au nombre du haut, puisque les deux nombres ont le même nombre de chiffres et à gauche, le chiffre des centaines de milliers du nombre du bas (9) est supérieur à celui du nombre du haut (4).
    • Poser correctement une opération suppose d'aligner les chiffres à partir de la droite. Si vous devez faire 912 - 5 000, n'allez pas aligner le 9 et le 5. Par contre, vous alignerez le 2 et le 0, puis vous alignerez en allant vers la gauche et comme le nombre du haut est plus court que celui du bas, vous lui ajouterez un 0, ce qui donne 0912. Ainsi, vous avez huit chiffres alignés deux à deux.
  9. Image intitulée Add and Subtract Integers Step 34
    9
    Inversez l'opération. Pour pouvoir faire l'opération, il faut poser la soustraction en inversant les nombres, le plus grand étant en haut, le signe ne change pas. Par contre, inscrivez immédiatement le signe « - » sur la ligne de réponse, à gauche. En effet, dans ce genre de soustractions, la réponse est négative. Dans un exercice scolaire, oublier de mettre le signe « - » vous priverait des points accordés à l'opération.
  10. Image intitulée Add and Subtract Integers Step 35
    10
    Faites la soustraction. Maintenant qu'elle est inversée et que vous avez mis le signe « - », vous n'avez plus qu'à faire les calculs en commençant par la droite. Il est impossible (et quand bien même ce serait possible, vous auriez une réponse fausse) de soustraire le grand nombre du petit.
    • Trouvez le résultat de la soustraction suivante : 968 772 - 415 990. Après avoir cherché, vérifiez la bonne réponse dans la section Conseils.
    Publicité

Méthode 5
Méthode 5 sur 5:
Additionner et soustraire des entiers négatifs

  1. Image intitulée Add and Subtract Integers Step 36
    1
    Sachez additionner un entier positif et un entier négatif. Ajouter un entier négatif revient à soustraire son opposé positif [8] . Bien sûr, on l'a vu, cela peut se faire sur une ligne graduée, mais au fil du temps, il faudra apprendre à se passer de ce qui n'est qu'une méthode pour débutant. Un entier négatif est spécial, dans la mesure où il est inférieur à 0 et à ce titre, sa valeur se doit d'être enlevée. Toute valeur à laquelle on ajoute un entier négatif est diminuée.
    • Exemple : 10 + (-3) = 10 - 3 = 7.
    • Exemple : -12 + 18 = 18 + (-12) = 18 – 12 = 6. Pour rappel, dans une somme, vous pouvez intervertir les nombres autant que vous voulez. Par contre, la chose n'est pas possible avec une soustraction.
  2. Image intitulée Add and Subtract Integers Step 37
    2
    Sachez quoi faire au cas où le premier nombre est inférieur au second. En utilisant la méthode précédente, il vous arrivera surement de tomber sur une soustraction bizarre, comme 4 – 7. En ce cas, vous prenez l'opposée de cette opération en mettant un signe « - ».
    • Supposons que vous ayez à calculer : 4 + (-7).
    • Transformez la somme en différence : 4 - 7.
    • Prenez l'opposée de la différence tout en inversant l'ordre des opérateurs :
      4 - 7 = -(7 – 4), ce qui donne comme résultat -(3) ou plus simplement -3.
    • Les parenthèses sont pratiques au début pour ne pas oublier le signe « - ». Dans le cas de 4 - 7, avec l'habitude, vous ferez mentalement 7 - 4, soit 3 et vous vous empresserez de mettre le signe « - », ce qui donne comme résultat - 3. Fatalement, un jour, vous oublierez le signe : nous sommes tous tombés dans ce piège !
  3. Image intitulée Add and Subtract Integers Step 38
    3
    Sachez comment l'on fait la somme de deux entiers négatifs. L'addition de deux nombres négatifs donne toujours un nombre négatif, encore plus petit. Dit autrement, vous obtenez un résultat qui est encore plus loin du 0 [9] . Prenons un exemple concret :
    • -3 + -6 =(-3) + (-6) = -3 - 6 = -9.
    • -15 + -5 = (-15) + (-5) = -15 - 5 = -20.
    • Comprenez-vous la démarche ? En fait, dans ce cas de figure, vous ajoutez les deux valeurs sans vous préoccuper du signe et vous mettez un signe « - », ce qui mathématiquement s'écrit : -4 + -3 = -(4 + 3) = -7.
  4. Image intitulée Add and Subtract Integers Step 39
    4
    Sachez comment soustraire un entier négatif. Comme vous l'avez vu, le plus souvent, il faut essayer de retomber sur une somme. Dans le cas de la soustraction d'un entier négatif, cela revient à ajouter son opposé positif. Avec de la pratique, vous vous ferez à cette façon d'opérer.
    • Si cela peut vous aider, pensez un nombre négatif comme de l’argent volé. Si vous réussissez à voler à un voleur une partie de l’argent qu’il vous a pris, vous avez moins perdu que si vous n’aviez rien fait : moins moins fait plus !
    • Exemple : 10 – (-5) = 10 + 5 = 15.
    • Exemple : -1 – (-2) = -1 + 2. À ce stade, vous retombez sur un cas de figure déjà vu (1re étape de cette méthode). Si vous ne maitrisez pas encore cette pratique, n'hésitez pas à relire ce qui a été écrit plus haut.
    • Voici la décomposition des différentes étapes de la résolution, résumées en une seule égalité : -1 – (-2) = -1 + 2 = 2 + (-1) = 2 – 1 = 1.
    Publicité

Conseils

  • Pour l'écriture des nombres supérieurs à 1 000, l'usage veut que l'on mette un espace tous les trois chiffres en commençant par la droite, comme dans 2 521 301. Certains mettent des points au lieu des espaces, le but, dans les deux cas, est de faciliter la lecture du nombre. En cas de doute, faites exactement comme vous le conseille votre professeur.
  • Pour les sommes proposées dans les 3e et 4e méthodes, les réponses sont les suivantes : 974 + 568 = 1 542 et 415 990 - 968 772 = -552 782.
  • Adaptez les lignes graduées à vos opérations. Ici, nous avons gradué pour les besoins de la démonstration les lignes en graduations d'une unité, mais rien ne vous empêche de les graduer de 10 en 10, de 1 000 en 1 000 ou de 100 000 en 100 000. La seule précaution à prendre est d'avoir des tirets également espacés. La façon de se déplacer sur cette nouvelle échelle graduée reste la même, simplement les nombres sont plus grands.
Publicité

wikiHows en relation

calculer l'inverse d'une matrice 3x3
Comment
calculer l'inverse d'une matrice 3x3
calculer un pourcentage d'augmentation
Comment
calculer un pourcentage d'augmentation
calculer le diamètre d'un cercle
Comment
calculer le diamètre d'un cercle
calculer la hauteur d'un triangle
Comment
calculer la hauteur d'un triangle
calculer la valeur de résistances en série ou en dérivation
Comment
calculer la valeur de résistances en série ou en dérivation
calculer un écart type
Comment
calculer un écart type
calculer le déterminant d'une matrice 3 x 3
Comment
calculer le déterminant d'une matrice 3 x 3
calculer le rayon d’un cercle
Comment
calculer le rayon d’un cercle
calculer la diagonale d’un rectangle
Comment
calculer la diagonale d’un rectangle
calculer la longueur de l'hypoténuse
Comment
calculer la longueur de l'hypoténuse
calculer un intervalle de confiance
Comment
calculer un intervalle de confiance
calculer les probabilités de gagner à la loterie
Comment
calculer les probabilités de gagner à la loterie
calculer une racine carrée à la main
Comment
calculer une racine carrée à la main
calculer l’angle entre deux vecteurs
Comment
calculer l’angle entre deux vecteurs
Publicité

Références

  1. ↑ https://www.mathopenref.com/integer.html
  2. ↑ https://www.splashmath.com/math-vocabulary/number-sense/number-line
  3. ↑ https://www.mathsisfun.com/definitions/natural-number.html
  4. ↑ https://www.khanacademy.org/math/arithmetic/arith-review-negative-numbers/arith-review-neg-num-intro/v/negative-numbers-introduction
  5. ↑ https://www.varsitytutors.com/hotmath/hotmath_help/topics/adding-and-subtracting-negatives
  6. ↑ https://www.khanacademy.org/math/arithmetic-home/negative-numbers/add-sub-neg-number-line/v/integer-equations-to-describe-diagram
  7. ↑ https://edu.gcfglobal.org/en/additionsubtraction/subtracting-two-and-threedigit-numbers/1/
  8. ↑ https://www.mathsisfun.com/positive-negative-integers.html
  9. ↑ https://www.wyzant.com/resources/lessons/math/elementary_math/positive_and_negative_numbers/adding_positive_and_negative_numbers

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 58 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 8 240 fois.
Catégories: Calculs
Publicité