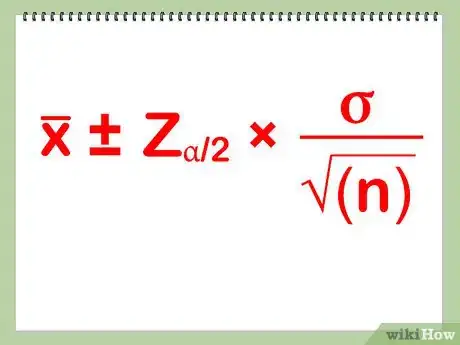Comment calculer un intervalle de confiance

En statistiques, un intervalle de confiance permet d'établir la marge d'erreur entre les données d'un sondage (échantillon) et les données de la population totale. En effet, si votre population est vaste (plusieurs milliers de données), il est plus rapide de travailler sur un échantillon et d'étendre les résultats à l'ensemble. Bien sûr, il y a risque d'erreur, d'où cet indicateur qu'est l'intervalle de confiance avec sa marge d'erreur. Si vous agissez méthodiquement, vous pourrez évaluer la marge d'erreur de telle ou telle affirmation portant sur un échantillon.

Étapes

1
Inscrivez le fait que vous voulez évaluer. Nous prendrons l'affirmation suivante : « Le poids moyen d'un étudiant de l'Université américaine ABC est de 180 livres (81,8 kg) ». L'objectif est d'évaluer, dans un certain intervalle de confiance, quel est le poids d'un étudiant à ABC.
2
Sélectionnez un échantillon parmi les 25 000 étudiants d'ABC. Pour les besoins de la démonstration, nous ne prendrons que 1 000 étudiants. C'est à partir de cet échantillon que se feront tous nos calculs.
3
Calculez la moyenne et l'écart type de cet échantillon. On peut choisir de calculer l'intervalle de confiance par rapport à une moyenne ou un écart type ou tout autre paramètre statistique d'une population donnée. Ici, nous nous limiterons à la moyenne et l'écart type.
- Pour calculer la moyenne de l'échantillon, il suffit d'additionner le poids des 1 000 étudiants sélectionnés et de diviser par 1 000. Admettons que nous trouvions 186 livres (84,5 kg).
- Pour calculer l'écart type du même échantillon, vous devez avoir la moyenne (c'est fait, c'est 186 livres). Ensuite, vous devez trouver la variance de l'échantillon, c'est-à-dire la moyenne des carrés des écarts à la moyenne. Ensuite, il suffit de prendre la racine carrée positive de cette variance. Posons que l'écart type des étudiants d'ABC est de 30 livres (si vous avez à résoudre un problème de mathématiques, cette valeur vous sera le plus souvent donnée).
4
Choisissez votre degré de confiance. Les degrés de confiance les plus couramment utilisés sont 90 %, 95 % et 99 % (ce degré peut vous être imposé dans le libellé de votre devoir de maths). Disons que, pour notre échantillon, nous prenions 95 %.
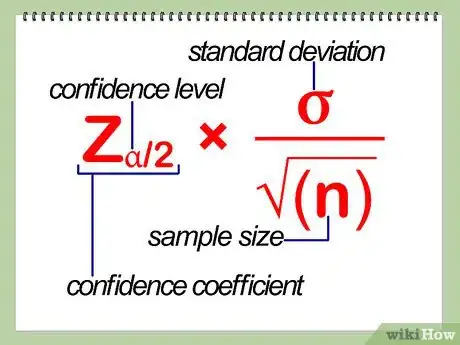
5
Calculez la marge d'erreur. Elle se calcule sur la base de cette formule : Z_a/2 x σ/√(n). Z_a/2 est le coefficient de confiance, avec a = degré de confiance, σ = écart type et n = taille de l'échantillon. En plus court, il faut multiplier la valeur critique par l'erreur type. Partant, pour notre échantillon, on peut donc décomposer la formule en deux parties.
- Le calcul de la valeur critique, soit Z_a/2 : on a choisi un degré de confiance de 95%, soit 0,95 si on convertit en chiffre décimal. On le divise par 2, ce qui donne 0,475. Ensuite, on prend une table de Z pour trouver la valeur qui correspond à 0,475. Cherchez 0,475 dans le tableau et vous lisez 1,9 dans la colonne de référence et 0,06 dans la ligne de référence, ce qui donne au final 1,96.
- Calculez l'erreur type. Prenez l'écart type 30 et divisez-la par la racine de la taille de l'échantillon (racine de 1000 = 31,6). On obtient au final 30/31,6, soit une erreur type de 0,95 livre.
- Multipliez 1,96 par 0,95 (valeur critique par erreur type) et cela vous donne votre marge d'erreur, soit 1,86.
6
Il ne reste plus qu'à établir l'intervalle de confiance. Pour le présenter, vous indiquez en premier la moyenne (180), suivi de ±, suivi de la marge d'erreur. Dans notre cas, cela donne : 180 ± 1,86. Si vous voulez un meilleur aperçu de votre intervalle, on peut faire les opérations pour trouver la limite inférieure (180 - 1,86 = 178,14 livres) et la limite supérieure (180 + 1,86 = 181,6 livres).
- Au final , la formule de l'intervalle de confiance est la suivante : x̅ ± Z_a/2*σ/√(n). Dans ce cas, x̅ représente la moyenne.
Publicité

Conseils

Les T-scores (ou scores T) et les Z-scores (ou scores T) peuvent se calculer à la main, mais aussi avec une calculatrice graphique ou des tables statistiques, que l'on trouve dans tout bon manuel de statistiques. Vous trouverez les Z-scores avec des calculateurs de distribution normale et les T-scores avec des calculateurs de distribution T. Ces calculateurs de probabilités se trouvent facilement sur Internet par exemple ici.
La population de votre échantillon doit avoir une dispersion normale pour que votre intervalle de confiance ait un quelconque sens.
La valeur critique utilisée qui sert à calculer la marge d'erreur est en fait une constante de type Z-score ou T-score. Ce dernier est de préférence utilisé lorsque l'écart type de la population est inconnu ou lorsque l'échantillon est petit.
Il existe de nombreuses autres méthodes pour tirer, à partir d'un échantillon, des donnes valables pour l'ensemble de la population de départ. Ainsi vous pouvez recourir à l'échantillonnage aléatoire simple, l'échantillonnage systématique, l'échantillonnage avec probabilité proportionnelle à la taille, l'échantillonnage stratifié, etc.
Un intervalle de confiance peut être contredit par des données particulières extrêmes. Par exemple, si vous êtes sûr à 95 % que la moyenne de votre échantillon de population est comprise entre 75 et 100, cela ne veut pas dire que vous avez 95 % de chances que la moyenne de l'ensemble de départ soit dans cet intervalle.