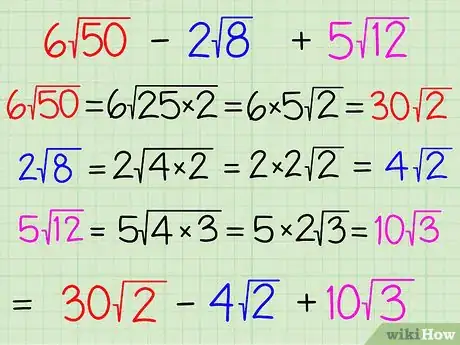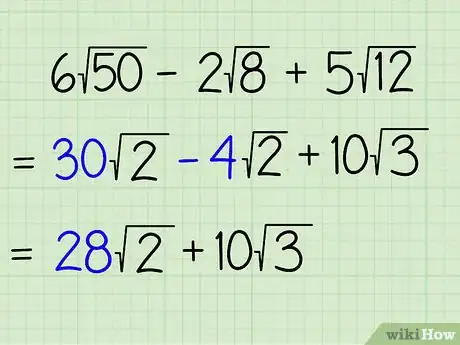Comment additionner ou soustraire des racines carrées

Informations concernant l'auteur.e

Quand on veut additionner ou soustraire entre eux des nombres contenant des racines carrées, il faut savoir qu’on ne peut le faire que s’il s’agit de la racine du même nombre. En clair, cela signifie que l’on peut additionner ou soustraire 2√3 avec 4√3, mais pas 2√3 avec 2√5. Bien souvent, on peut en fait simplifier le nombre qui se trouve sous la racine pour pouvoir ensuite sans problème procéder à des calculs.

Partie 1

Partie 1 sur 2:
Comprendre les bases

1
Simplifiez les nombres sous la racine si possible. Pour cela, essayez de factoriser le nombre sous la racine pour trouver au moins un facteur qui sera un carré parfait, comme 25 (5 x 5) ou 9 (3 x 3). Une fois que c’est fait, prenez la racine du nombre qui est un carré parfait et sortez-la de la racine. Il n’y aura alors plus que le facteur restant sous celle-ci. Prenons à titre d’exemple la somme 6√50 - 2√8 + 5√12. Les nombres qui sont à l’extérieur des racines sont appelés « coefficients » et ceux qui sont dessous sont des « radicandes ». Vous pouvez simplifier chacun des termes de cette somme ^{[1]
X
Source de recherche}.
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Dans cette partie, vous avez factorisé "50" pour le transformer en "25 x 2", et vous avez ensuite sorti le "5", qui est la racine du carré parfait "25", pour le placer devant le radical. Seul le "2" est resté sous la racine. Enfin, vous avez multiplié ce "5" par le "6" qui était déjà avant la racine, et 30 est devenu le nouveau coefficient.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Dans cette partie, vous avez factorisé "8" pour le transformer en "4 x 2", et vous avez ensuite sorti le "2", qui est la racine du carré parfait "4", pour le placer devant le radical. Seul le "2" est resté sous la racine. Enfin, vous avez multiplié "2" par le "2"qui était déjà devant la racine, et 4 est devenu le nouveau coefficient.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Dans cette partie, vous avez factorisé "12" pour le transformer en "4 x 3", et vous avez ensuite sorti le "2", qui est la racine du carré parfait "4", pour le placer devant le radical. Seul le "3" est resté sous la racine. Enfin, vous avez multiplié ce "2" par le "5" qui était déjà avant la racine, et 10 est devenu le nouveau coefficient.
2
Entourez les termes ayant des radicandes identiques. Lorsque vous avez simplifié les radicandes, vous obtenez la somme sous la forme suivante : 30√2 - 4√2 + 10√3. Étant donné que ce sont les seuls que vous avez le droit de soustraire ou d’additionner, vous pouvez entourer les termes dont le radical est le même pour mieux les repérer. Dans notre exemple, ce sera 30√2 et 4√2. Voyez cela un peu comme une somme de fractions, qui elles aussi ne peuvent être additionnées ou soustraites les unes aux autres que si elles ont un dénominateur commun.
3
Soyez méthodique. Si vous faites un calcul plus long dans lequel on retrouve plusieurs groupes de radicandes identiques, commencez par entourer la première série, puis soulignez la deuxième, mettez un astérisque à la troisième, et ainsi de suite. Si cela vous aide à ne rien oublier, placez les termes dans un ordre différent afin que tous ceux qui ont le même radicande soient côte à côte.
4
Additionnez ou soustrayez. Arrivé à ce stade, il ne vous reste plus qu’à procéder au calcul en faisant la somme de tous les termes qui partagent le même radicande, et en laissant de côté tous les autres. Vous ne devez pas combiner des radicandes différents. Un terme qui ne peut pas être associé à aucun autre reste tout simplement tel quel. Voici ce que cela donne avec notre exemple :
- 30√2 - 4√2 + 10√3 =
- (30 - 4)√2 + 10√3 =
- 26√2 + 10√3
Publicité

Partie 2

Partie 2 sur 2:
S’entrainer

1
Faites l’exemple 1. Dans cet exemple, vous cherchez à calculer √(45) + 4√5. Nous vous expliquons comment procéder.
- Simplifiez √(45). Vous pouvez tout d’abord factoriser cette partie pour avoir √(9 x 5).
- Ensuite, vous pouvez sortir "3", puisque c’est la racine du carré parfait "9", et en faire le coefficient de la racine. On se retrouve avec √(45) = 3√5.
- Pour finir, vous n’avez plus qu’à ajouter les deux coefficients ayant le même radicande pour trouver le résultat : 3√5 + 4√5 = 7√5.
2
Faites l’exemple 2. Il s’agit du problème suivant : 6√(40) - 3√(10) + √5. Voyons comment procéder dans ce cas.
- Simplifiez 6√(40). Commencez par factoriser "40" pour obtenir "4 x 10", ce qui nous donne 6√(40) = 6√(4 x 10).
- Ensuite, sortez le "2" qui est la racine du carré parfait "4", puis multipliez-le par le coefficient déjà présent. Vous vous retrouvez avec 6√(4 x 10) = (6 x 2)√10.
- Multipliez les deux coefficients. Cela donne 12√10.
- Votre problème se présente maintenant sous la forme 12√10 - 3√(10) + √5. Comme vous avez deux termes qui ont les mêmes radicandes, vous pouvez les soustraire l’un à l’autre et laisser le troisième tel qu’il est.
- Vous arrivez donc à (12-3)√10 + √5, qui peut être simplifié en 9√10 + √5.
3
Faites l’exemple 3. C’est la somme suivante : 9√5 -2√3 - 4√5. Il s’agit d’un cas où aucun des termes ne peut être réécrit avec un carré parfait, aucune simplification n’est donc possible. Cependant, le premier et le troisième terme ont déjà le même radicande, nous avons donc le droit de les combiner (9 - 4). Leur radicande reste inchangé. Le terme restant est différent, la réponse au problème est donc 5√5 - 2√3.
4
Faites l’exemple 4. Imaginons que vous deviez résoudre √9 + √4 - 3√2.
- Puisque √9 est égale à √(3 x 3), vous pouvez simplifier √9 en 3.
- Puisque √4 est égale à √(2 x 2), vous pouvez simplifier √4 en 2.
- À ce stade, vous pouvez simplement ajouter 3 + 2 qui font 5.
- Comme 5 et 3√2 ne sont pas des termes identiques, vous ne pouvez rien faire de plus. Vous réponse sera donc 5 - 3√2.
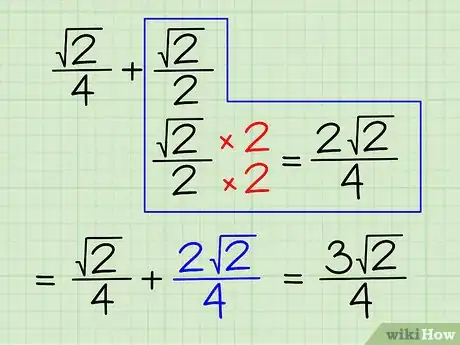
5
Faites l’exemple 5. Essayons maintenant d’ajouter ou de soustraire des racines qui se trouvent à l’intérieur d’une fraction. Vous le savez déjà, pour ce qui est des fractions, on peut les additionner ou les soustraire uniquement si elles ont le même dénominateur. Intéressons-nous à cette somme: (√2)/4 + (√2)/2. La marche à suivre est un peu plus délicate.
- Donnez à tous les termes un dénominateur commun. Le plus petit dénominateur commun, c’est-à-dire le dénominateur qui donne un nombre entier quand il est divisé par "4" ou "2", est "4".
- En ce qui concerne le deuxième terme, (√2)/2, pour qu’il ait pour dénominateur 4, vous devez multiplier le dénominateur et le numérateur par 2/2. (√2)/2 x 2/2 = (2√2)/4.
- Ajoutez ensuite les numérateurs des deux fractions en gardant le dénominateur commun inchangé. Procédez exactement de la même façon que lorsque vous faites habituellement des sommes de fractions. (√2)/4 + (2√2)/4 = (3√2)/4.
Publicité

Conseils

Commencez toujours par simplifier tous les radicandes qui peuvent avoir pour facteur des carrés parfaits avant de vous lancer dans la recherche et dans la somme de radicandes identiques.

Avertissements

Ne faites jamais la somme de racines qui ne sont pas les mêmes.
Vous ne devez jamais faire la somme d’une racine et d’un nombre entier. Cela signifie que 3 + (2x)^1/2 ne peut pas être simplifié.
- Remarque : dire "(2x) à la puissance = (2x)^1/2 " revient au même que de dire "racine carrée de (2x)".