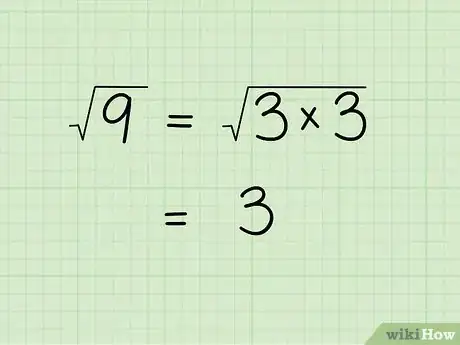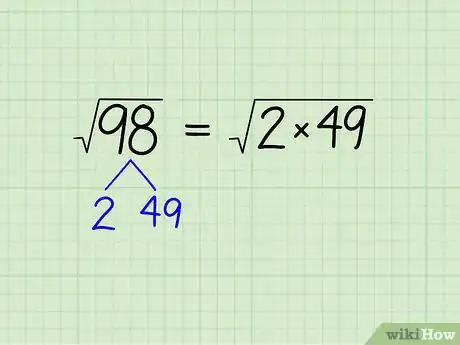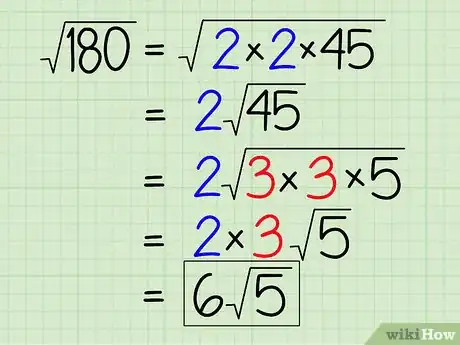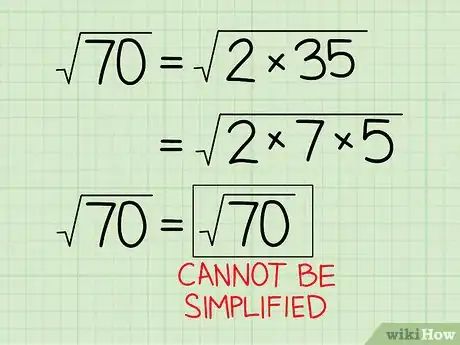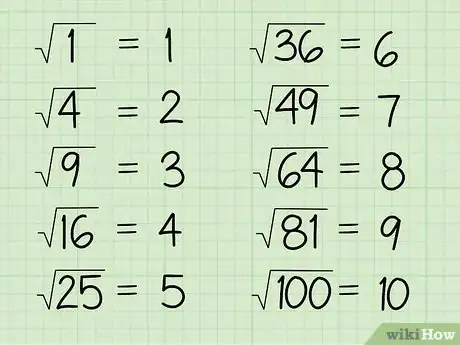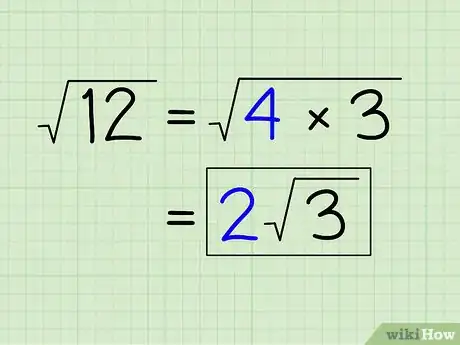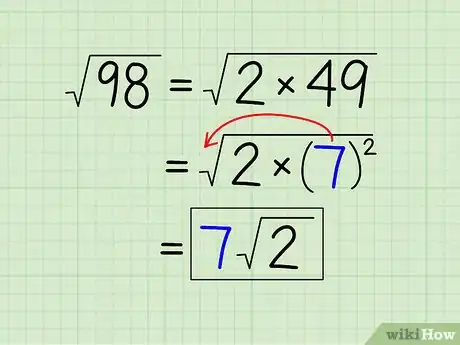Comment simplifier une racine carrée

Coécrit par David Jia

Une racine carrée n'est pas compliquée. Il faut factoriser le radicande de façon à faire apparaitre, si possible, un carré parfait, à la suite de quoi on peut sortir ce dernier de la racine. Il vous faut donc connaitre quelques carrés parfaits, apprendre à factoriser et vous saurez simplifier une racine carrée.

Méthode 1

Méthode 1 sur 3:
Simplifier une racine en factorisant

1
Comprenez bien ce qu'est la factorisation. En général, quand on simplifie une racine carrée, c'est pour la rendre plus facile à manipuler, lors de calculs ultérieurs par exemple. La factorisation consiste à décomposer un nombre en facteurs, premiers ou non. Ainsi, 9 = 3 x 3. Une fois la décomposition faite, on peut récrire la racine sous forme simplifiée (souvent, mais pas toujours !), parfois même la transformer en nombre entier. Ainsi, √9 = √(3x3) = 3. C'est un exemple simple, passons maintenant à des exemples plus compliqués.
2
Divisez le radicande successivement par des nombres premiers croissants. Si votre radicande est pair, divisez-le par 2. S'il est impair, essayez 3. Si votre radicande finit par 5 ou 0, divisez-le par 5. Si rien ne marche, essayez les nombres premiers suivants jusqu'à en trouver un. Si on teste uniquement les nombres premiers, c'est que les autres sont des combinaisons de ces nombres. Ainsi, il est inutile de chercher à diviser un radicande par 4, s'il n'est pas pair au départ. Voici les premiers nombres… premiers :
- 2
- 3
- 5
- 7
- 11
- 13
- 17
3
Récrivez votre radicande sous la forme d'un produit (multiplication). Pour l'instant, vous ne devez rien sortir de la racine, mais trouvez les facteurs du radicande. Par exemple, voyez si on peut simplifier √98. Cherchez les facteurs premiers : 98 ÷ 2 = 49 ou pour notre propos : 98 = 2 x 49. Remplacez « 98 » sous le signe de la racine par 2 x 49 : √98 = √(2 x 49).
4
Refaites la même chose avec le nombre restant. On ne simplifiera que lorsqu'on aura tout décomposé en facteurs premiers et en carrés parfaits. En effet, seuls les carrés parfaits peuvent être sortis de la racine : l'expression √(2 x 2) équivaut « au nombre qui multiplié par lui-même vaut 2 x 2 ». La réponse est certes évidente ici, puisque c'est … 2 ! Si vous avez bien compris, on peut revenir à notre exemple √(2 x 49).
- 2 a déjà été mis en facteur (c'est un des nombres premiers de la liste). On va pour l'instant l'ignorer et s'intéresser à 49.
- 49 n'est divisible ni par 2, ni par 3, ni par 5. Vous pouvez vérifier ! Il faut continuer à chercher avec les nombres premiers suivants.
- 49 n'est divisible que par 7 : 49 ÷ 7 = 7, donc 49 = 7 x 7.
- Reformulez alors la racine : √(2 x 49) = √(2 x 7 x 7).
5
Simplifiez en « sortant » le carré parfait. Si, en radicande, vous avez deux facteurs identiques, vous allez pouvoir le sortir de la racine, les autres restants en radicande. Ainsi, √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).
- Même s'il est théoriquement possible de décomposer entièrement un radicande en facteurs premiers, il est inutile d'aller aussi loin dès lors que vous avez déjà trouvé des carrés parfaits. Par exemple, √(16) = √(4 x 4) = 4. Cette décomposition est suffisante, car on a une réponse. On aurait pur faire : √(16) = √(4 x 4) = √(2 x 2 x 2 x 2) = √(2 x 2) x √(2 x 2) = 2 x 2 = 4. Vous le voyez, c'est plus long !
6
S'il y en a plusieurs, multipliez entre eux les entiers (coefficients) sortis de la racine. Quand le radicande est grand, cela arrive souvent. Il y a plusieurs simplifications à faire. Si c'est le cas, multipliez au fur et à mesure de leur apparition les entiers issus de la racine. Prenons l'exemple de √180 :
- √180 = √(2 x 90)
- √180 = √(2 x 2 x 45)
- √180 = 2√45, mais l'on peut encore simplifier
- √180 = 2√(3 x 15)
- √180 = 2√(3 x 3 x 5)
- √180 = (2)(3√5)
- √180 = 6√5
7
Inscrivez « racine irréductible » si vous ne trouvez aucun carré parfait lors de la décomposition. En effet, il se peut que vous tombiez sur des racines déjà réduites à leur plus simple expression, elles sont dites « irréductibles ». Si vous décomposez entièrement le radicande en nombres premiers, tous différents les uns des autres, alors vous avez affaire à une racine irréductible. Mauvais signe ! Prenons l'exemple de √70 :
- comme 70 = 35 x 2, alors √70 = √(35 x 2) ;
- comme 35 = 7 x 5, alors √(35 x 2) = √(7 x 5 x 2) ;
- ces trois facteurs sont des nombres premiers, tous différents, il n'y a aucun carré parfait : la racine ne peut être simplifiée.
Publicité

Méthode 2

Méthode 2 sur 3:
Connaitre quelques carrés parfaits

1
Apprenez par cœur quelques carrés parfaits ainsi que leurs racines associées. Élever un nombre au carré (le multiplier par lui-même) donne un carré parfait. Par exemple, 25 est un carré parfait, car 5 x 5 (= 5²) donne 25. Il est bon de connaitre les dix premiers carrés parfaits ainsi que leurs racines associées, cela vous aidera grandement pour simplifier de grands nombres. Voici la liste des premiers :
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
- 6² = 36
- 7² = 49
- 8² = 64
- 9² = 81
- 10² = 100
2
Trouvez la racine carrée d'un carré parfait. Si vous repérez un de ces carrés parfaits sous une racine, c'est simple : vous enlevez le signe √ et vous inscrivez le nombre de départ. Ainsi, si vous voyez 25 en radicande, vous savez tout de suite que la réponse sera 5, car 25 est le carré de 5. Voici la liste des premières racines, à savoir progressivement par cœur :
- √1 = 1
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
- √36 = 6
- √49 = 7
- √64 = 8
- √81 = 9
- √100 = 10
3
Factorisez le radicande en sorte d'avoir au moins un carré parfait. Au moment de la factorisation, soyez attentif à l'apparition éventuelle d'un carré parfait. Vous gagnerez ainsi beaucoup de temps pour simplifier. Voici quelques exemples.
- √50 = √(25 x 2) = √(5 x 5 x 2) = 5√2. Si l'un des facteurs se termine par 25, 50 ou 75, vous pouvez au minimum sortir 5 de la racine.
- √1700 = √(100 x 17) = √(10 x 10 x 17) = 10√17. Si l'un des facteurs se termine par 00, vous pouvez au minimum sortir 10 de la racine.
- √72 = √(9 x 8) = √(3 x 3 x 8) = 3√8. Essayez toujours de voir si 9 ne serait pas un des facteurs. Il existe une astuce pour savoir si un nombre est divisible par 9 : il suffit d'additionner tous les chiffres de ce nombre et si la somme est 9, alors votre nombre est un multiple de 9.
- √12 = √(4 x 3) = √(2 x 2 x 3) = 2√3. Il faut aussi essayer de voir si le radicande n'est pas divisible par 4. Il n'y a pas d'astuce particulière, mais, avec de petits radicandes, on voit rapidement s'il est divisible. En conclusion, retenez bien tous ces petits conseils pour aller droit au but.
4
Vérifiez que le radicande n’est pas le produit de plusieurs carrés parfaits. Si vous en trouvez plusieurs, sortez-les de la racine au fur et à mesure. Une fois la racine devenue irréductible, multipliez les coefficients sortis de la racine. Prenons l'exemple de √72 :
- √72 = √(9 x 8)
- √72 = √(9 x 4 x 2)
- √72 = √(9) x √(4) x √(2)
- √72 = 3 x 2 x √2
- √72 = 6√2
Publicité

Méthode 3

Méthode 3 sur 3:
Quelques éléments de terminologie

1
Le symbole radical. C'est le « symbole » de la racine carrée (√). Exemple : dans √25, « √ » est le symbole radical.
2
Le radicande. C'est le nombre qui se trouve sous la racine carrée, celui dont vous essayez de trouver la racine. Dans √25, « 25 » est le radicande.
3
Le coefficient. Dans certains problèmes, c'est le nombre qui multiplie une racine carrée (il se trouve à gauche de la racine carrée). Dans 7√2, « 7 » est le coefficient.
4
Un facteur. C'est un nombre qui divise parfaitement un autre (le reste de cette division doit être 0). Par exemple, 2 est un facteur de 8, car 8 ÷ 4 = 2, mais 3 n'en est pas un, car 8 ÷ 3 = 2,66..., lequel n'est pas un nombre entier. Autre exemple, 5 est un facteur de 25, car 5 x 5 = 25.
5
La simplification d'une racine carrée. L'objectif consiste à faire apparaitre un carré parfait sous la racine, à le sortir de sa position de radicande pour le mettre à gauche du symbole racine et à laisser les autres facteurs sous le symbole radical. Si votre radicande est un carré parfait, le signe de la racine disparait. Ainsi √98 devient 7√2 et √25 devient 5.

Publicité

Conseils

Pour trouver le carré parfait qui divise votre radicande, vous pouvez commencer par le carré parfait le plus proche du radicande, puis vous diminuez progressivement jusqu'à trouver un éventuel diviseur. Par exemple, vous cherchez un carré parfait qui diviserait 27, vous commencez par 25 (cela ne marche pas !), puis 16 (cela ne marche pas !), puis 9. Stop ! Il est là : 9 divise 27 ! D'autres utilisent la méthode inverse : on commence par 1 et l'on remonte, 4, 9… Le résultat est identique.

Avertissements

Simplifier ne veut pas dire calculer ! À aucun moment, durant ces étapes, vous ne devriez obtenir de nombres décimaux !
Les calculatrices sont certes très utiles, surtout si vous devez extraire la racine d'un grand nombre, mais habituez-vous à vous en passer. Vous verrez qu'avec de la pratique, il est très facile et rapide d'extraire une racine.