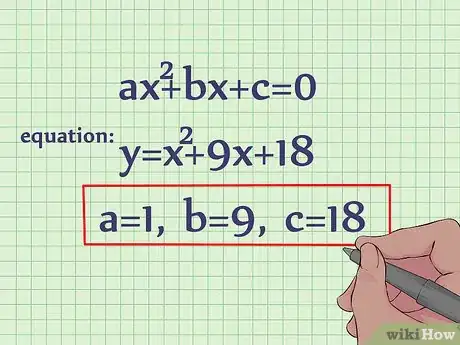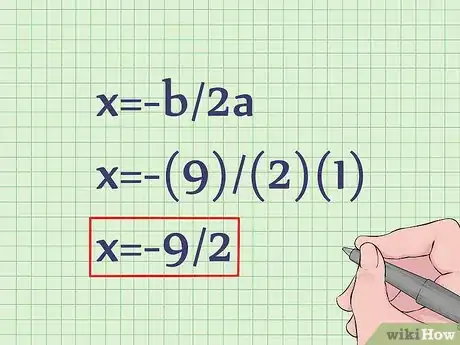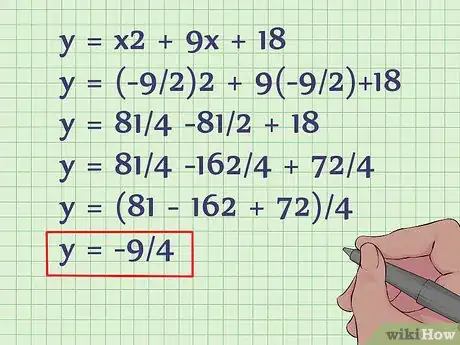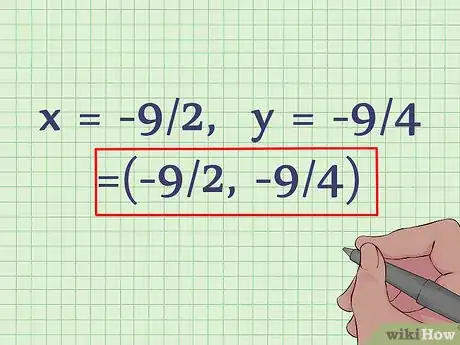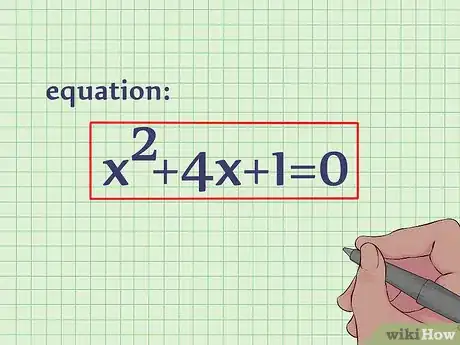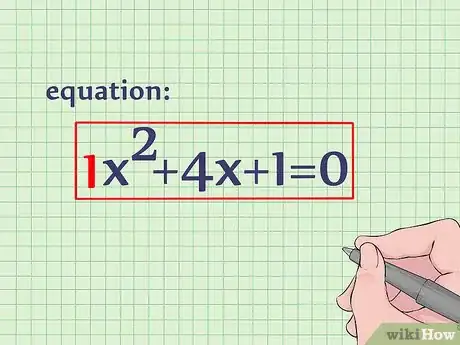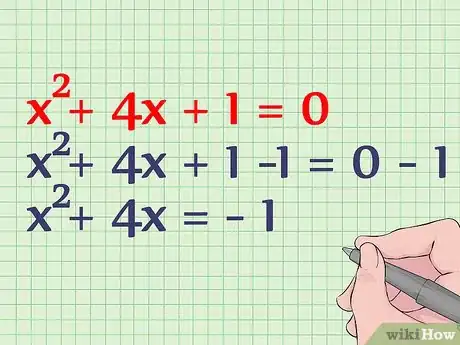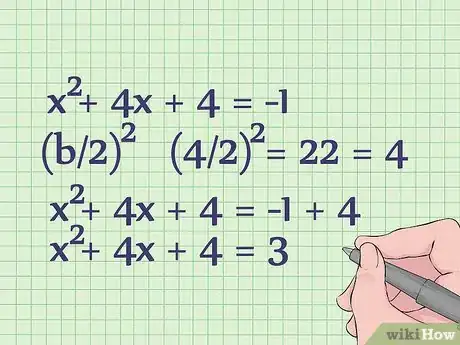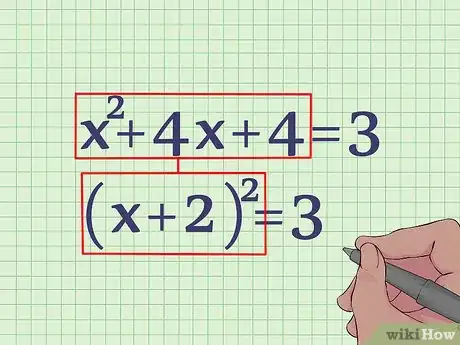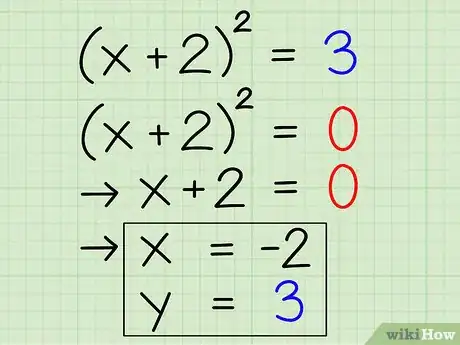Comment trouver le sommet d'une parabole d'une équation du second degré

Informations concernant l'auteur.e

Le sommet de la parabole, issue d’une équation du second degré (aussi appelée fonction), est le point où la parabole atteint soit un maximum, soit un minimum. Ce point particulier se situe sur l’axe de symétrie de la parabole, c’est-à-dire que la partie de courbe qui se trouve à gauche de cet axe se retrouve à l’identique, mais inversée (effet miroir) à droite. Pour trouver ce sommet, deux solutions : soit utiliser une formule, soit compléter le carré.

Méthode 1

Méthode 1 sur 2:
Trouver le sommet en utilisant la formule classique

1
Commencez par identifier les valeurs de a, b et c. Une équation du second degré se présente sous la forme y = a x² + bx + c, c est la constante (terme sans inconnue). Pour cet article, nous prendrons l’équation y = x ² +9 x +18. Dans ce cas, a = 1, b = 9 et c = 18 ^{[1]
X
Source de recherche}.
2
Trouvez d’abord l’abscisse du sommet de la parabole. Il est aussi appelé axe de symétrie de la courbe. Utilisez la formule x = -b/2a. Remplacez les valeurs de a et b, ce qui donne :
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
3
Trouvez l’ordonnée du sommet de la parabole. Pour ce faire, mettez x dans l’équation de départ. Le sommet de la parabole a pour coordonnées (x, y) = [(-b/2a), f(-b/2a)]. Ici, pour trouver y, il faut juste faire f(9/2), ce qui donne :
- y = x² + 9x + 18
- y = (-9/2)² + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72)/4
- y = -9/4
4
Inscrivez le résultat sous forme de paire ordonnée (x, y). Dans notre exemple, x = -9/2 et y = -9/4, ce qui, en paire ordonnée, donne : (-9/2, -9/4). Le sommet de la parabole a pour coordonnées (-9/2, -9/4). Sur la courbe, ce point sera au bas de la parabole, c’est ce qu’on appelle un minimum, car la parabole s’ouvre le haut. En effet, le coefficient de x² est positif.

Publicité

Méthode 2

Méthode 2 sur 2:
Trouver le sommet en complétant le carré

1
Écrivez votre équation. Avec la méthode qui consiste à compléter le carré, on peut trouver le sommet d’une parabole, graphe d’une équation du second degré. L’avantage de cette méthode est qu’on trouve directement x et y (coordonnées de ce sommet) sans avoir à passer par l’application numérique vue dans l’exemple précédent. Pour cet article, nous prendrons l’équation : x² + 4x + 1 = 0 ^{[2]
X
Source de recherche}.
2
Divisez chaque terme par le coefficient du terme de x². Dans notre cas, c’est 1. On passe à l’étape suivante, car tout diviser par 1 revient... à ne rien changer.
3
Déplacez la constante dans le membre de droite de l’équation. La constante est le terme qui n’est pas affecté à une puissance de x. Ici, la constante est 1. Ajoutez -1 à chacun des membres de l’équation. On obtient donc ^{[3]
X
Source de recherche} :
- x² + 4x + 1 = 0
- x² + 4x + 1 -1 = 0 - 1
- x² + 4x = - 1
4
Complétez le carré à gauche. Calculez (b/2)² et ajoutez ce résultat de chaque côté de l’équation. Ici, b = 4 (c’est le 4 de 4x).
- (4/2)² = 2² = 4. À présent, ajoutez ce 4 de chaque côté de l’équation :
  - x² + 4x + 4 = -1 + 4
  - x² + 4x + 4 = 3
5
Factorisez le membre de gauche. x² + 4x + 4 est une identité remarquable, c’est en fait (x + 2)². Notre équation ressemble alors à ça : (x + 2)² = 3.
6
Prenez cette équation pour trouver les coordonnées x et y du sommet. Pour trouver x, il faut résoudre l’équation suivante : (x + 2)² = 0. La réponse est simple et unique : c’est -2, car (-2+2) = 0. Votre sommet a pour abscisse x = -2. Quant à l’ordonnée y, rien de plus simple ! C’est la valeur du 2e membre de l’équation de départ : y = 3. On peut aller encore plus vite pour x, on prend la valeur opposée à la valeur qui se trouve dans la parenthèse. Au final, la parabole (de la fonction f(x)=x² + 4x + 1) a son sommet au point de coordonnées (-2, 3).

Publicité

Conseils

Identifiez correctement a, b et c.
Regardez toujours bien votre courbe. Non seulement cela vous aide à comprendre ce que vous faites, mais vous pourrez voir si vous faites des erreurs.
L’ordre des opérations doit être scrupuleusement suivi pour obtenir un résultat correct.