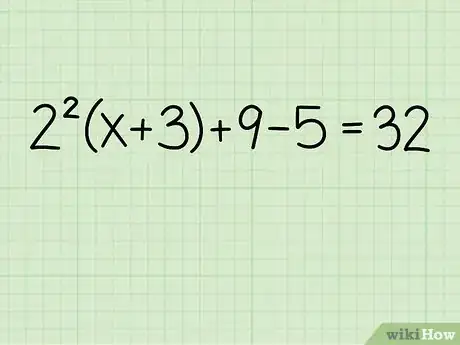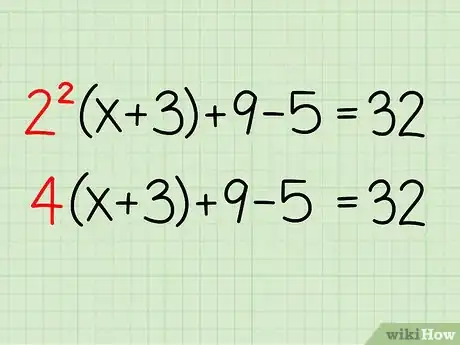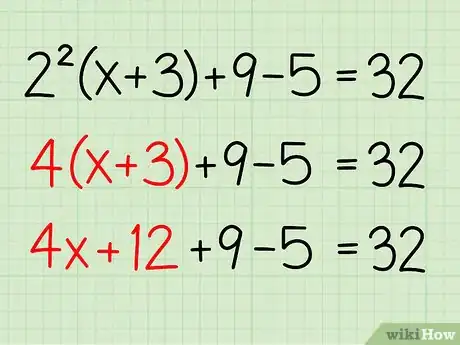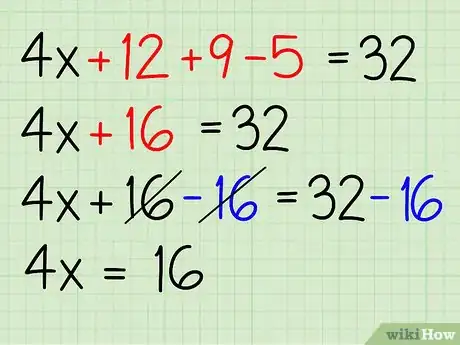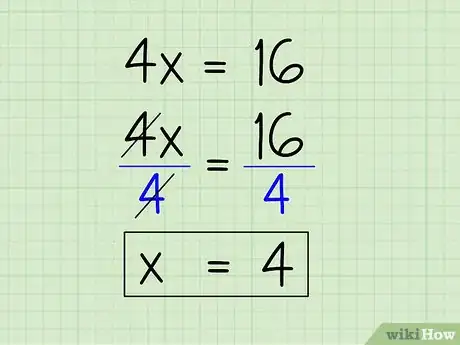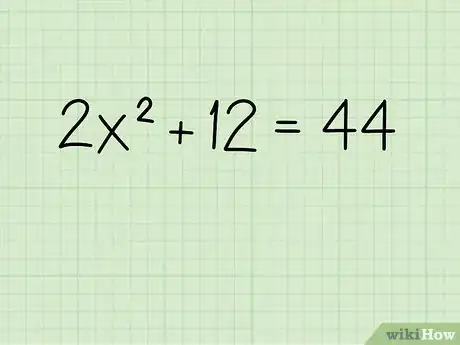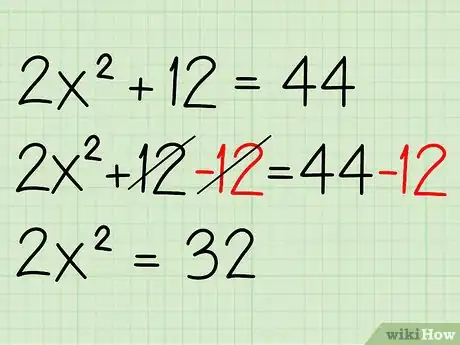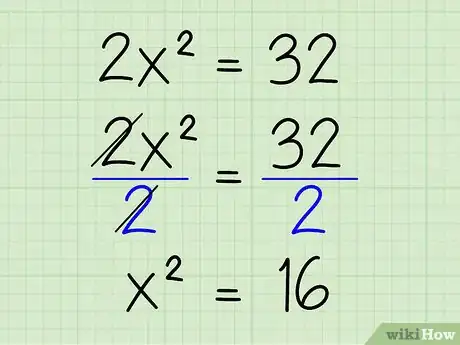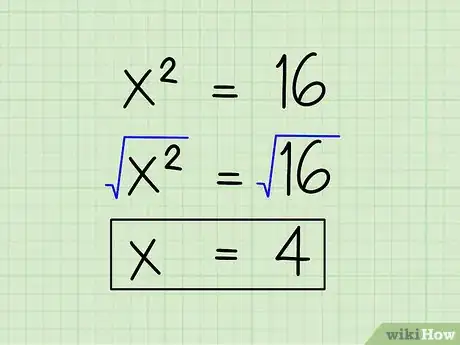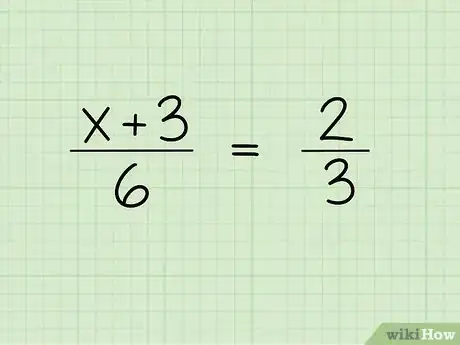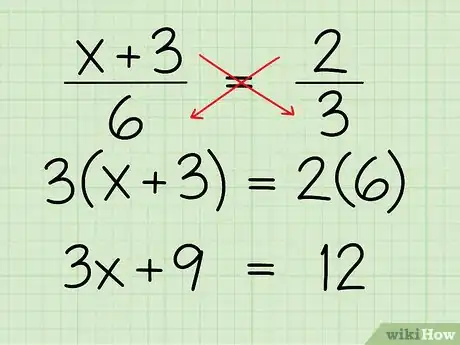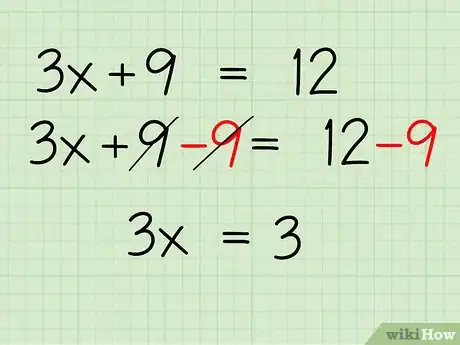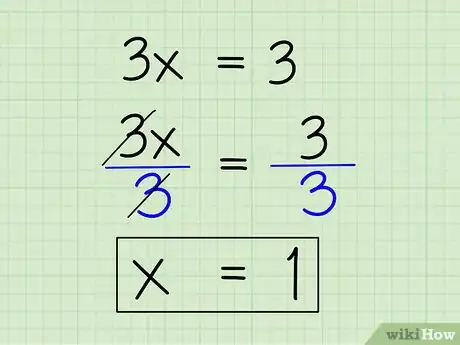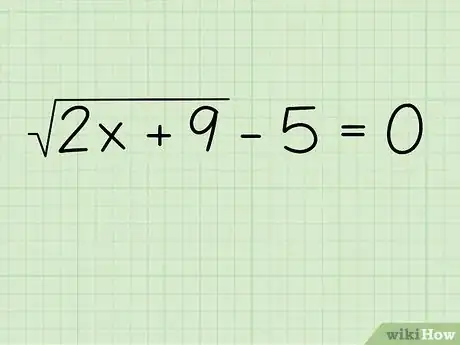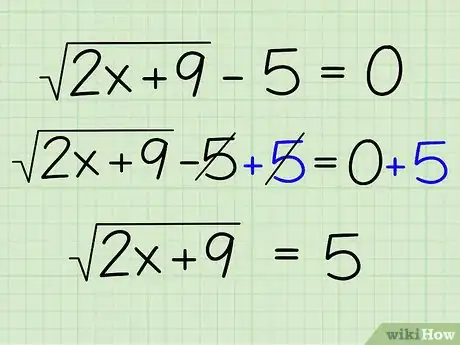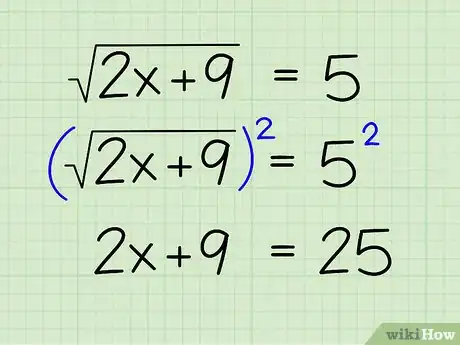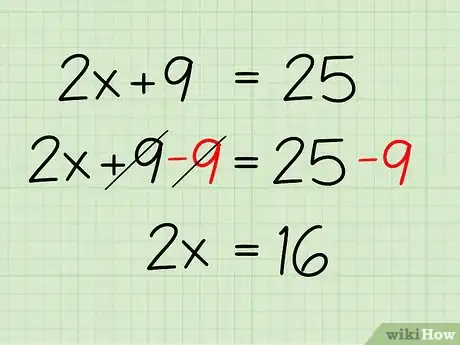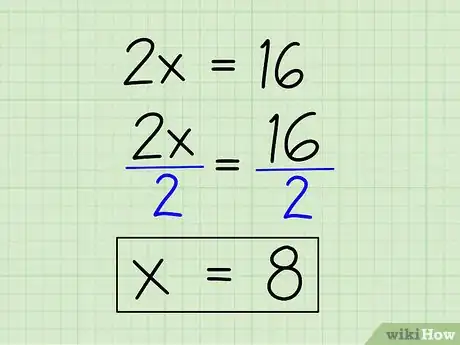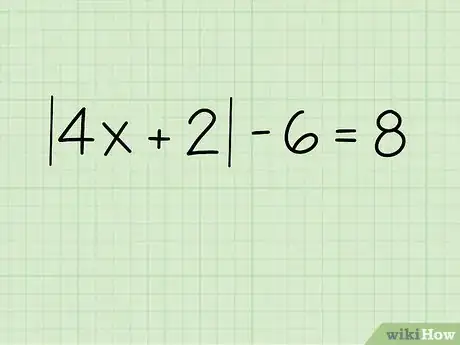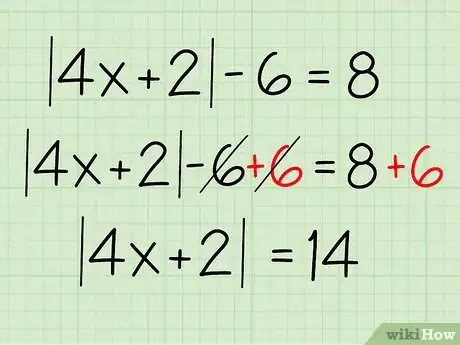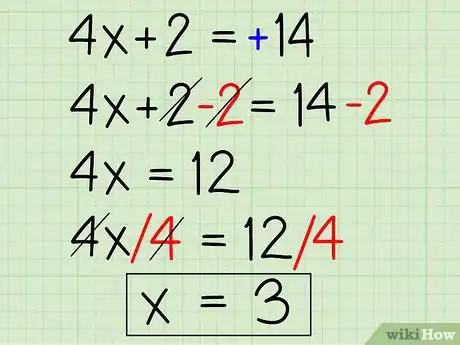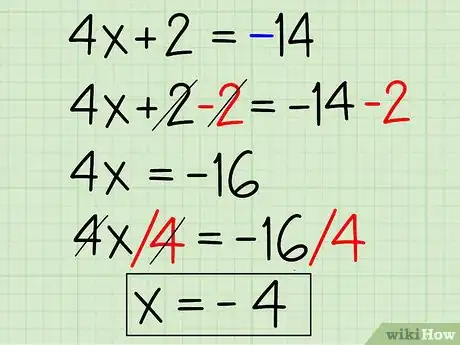Comment trouver X

Coécrit par David Jia

Il existe de nombreuses méthodes pour trouver la valeur de x au sein d'une équation, qu'il s'agisse d'équations complexes comprenant des exposants ou des racines ou d'équations simples ne nécessitant que quelques divisions ou multiplications. Quelle que soit la méthode utilisée, vous devrez toujours trouver un moyen d'isoler x d'un côté de l'équation afin d'en déterminer la valeur.

Méthode 1
Méthode 1 sur 5:
Équation du premier degré classique

  1. Image intitulée Solve for X Step 1
    1
    Posez le problème. Prenons l'exemple suivant :
    • 22(x+3) + 9 - 5 = 32
  2. Image intitulée Solve for X Step 2
    2
    Calculez la valeur avec l'exposant. Pour se souvenir de l'ordre des opérations en mathématiques, on peut retenir le mot mnémotechnique PEMDAS, soit Parenthèses, Exposants, Multiplication/Division et Addition/Soustraction. Dans notre cas, on ne peut commencer par les parenthèses, puisque x est à l'intérieur. On commence donc par régler les exposants : 22. 22 = 4
    • 4(x+3) + 9 - 5 = 32
  3. Image intitulée Solve for X Step 3
    3
    Faites la multiplication. Multipliez chaque terme de la parenthèse (x + 3) par 4. Voici comment procéder :
    • 4x + 12 + 9 - 5 = 32
  4. Image intitulée Solve for X Step 4
    4
    Faites les additions et soustractions. Additionnez et soustrayez les nombres restants. Voici comment faire :
    • 4x+21-5 = 32
    • 4x+16 = 32
    • 4x + 16 - 16 = 32 - 16
    • 4x = 16
  5. Image intitulée Solve for X Step 5
    5
    Isolez l'inconnue. Pour cela, divisez simplement chacun des côtés de l'équation par 4 pour trouver x. 4x/4 = x et 16/4 = 4, donc x = 4.
    • 4x/4 = 16/4
    • x = 4
  6. Image intitulée Solve for X Step 6
    6
    Vérifiez vos calculs. Pour cela, il suffit de réintroduire x = 4 dans l'équation d'origine pour vous assurer que cela fonctionne. Voici comment vous y prendre :
    • 22(x+3)+ 9 - 5 = 32
    • 22(4+3)+ 9 - 5 = 32
    • 22(7) + 9 - 5 = 32
    • 4(7) + 9 - 5 = 32
    • 28 + 9 - 5 = 32
    • 37 - 5 = 32
    • 32 = 32
    Publicité

Méthode 2
Méthode 2 sur 5:
Équation avec des puissances

  1. Image intitulée Solve for X Step 7
    1
    Posez le problème. Imaginons un exemple où le terme x est élevé à une puissance :
    • 2x2 + 12 = 44
  2. Image intitulée Solve for X Step 8
    2
    Isolez le terme en x comportant la puissance. La première chose à faire est de combiner les termes similaires de sorte que les constantes se retrouvent à droite de l'équation tandis que les termes avec exposant se retrouveront à gauche. Soustrayez la valeur 12 des deux côtés de l'équation. Voici comment faire :
    • 2x2+12-12 = 44-12
    • 2x2 = 32
  3. Image intitulée Solve for X Step 9
    3
    Isolez l'inconnue avec l'exposant en divisant les deux côtés de l'équation par le terme en x. Dans notre cas, le terme en x est égal à 2, alors divisez les deux côtés de l'équation par 2 pour vous en débarrasser. Voici ce que cela donne :
    • (2x2)/2 = 32/2
    • x2 = 16
  4. Image intitulée Solve for X Step 10
    4
    Prenez la racine carrée des deux parties de l'équation. Le fait de prendre la racine carrée de x2 va faire disparaitre l'exposant. Alors, élevez les deux côtés au carré. Ainsi, vous obtiendrez x d'un côté de l'équation et la racine carrée de 16, soit 4, de l'autre côté. Au final, x = 4.
  5. Image intitulée Solve for X Step 11
    5
    Vérifiez vos calculs. Réintroduisez x = 4 dans l'équation d'origine pour vous assurer de bien retomber sur vos pattes. Voici comment faire :
    • 2x2 + 12 = 44
    • 2 x (4)2 + 12 = 44
    • 2 x 16 + 12 = 44
    • 32 + 12 = 44
    • 44 = 44
    Publicité

Méthode 3
Méthode 3 sur 5:
Équation avec des fractions

  1. Image intitulée Solve for X Step 12
    1
    Posez le problème. Prenons l'exemple suivant [1]  :
    • (x + 3)/6 = 2/3
  2. Image intitulée Solve for X Step 13
    2
    Faites le produit en croix. Pour cela, il suffit de multiplier le numérateur d'une des fractions par le dénominateur de l'autre fraction. En gros, vous allez faire une multiplication en diagonale. Multipliez le premier dénominateur, 6, par le second numérateur, 2, pour obtenir 12 du côté droit de l'équation. Multipliez le second dénominateur, 3, par le premier numérateur, x + 3, pour obtenir 3 x + 9 du côté gauche de l'équation. Voici ce que cela donne :
    • (x + 3)/6 = 2/3
    • 6 x 2 = 12
    • (x + 3) x 3 = 3x + 9
    • 3x + 9 = 12
  3. Image intitulée Solve for X Step 14
    3
    Combinez les termes similaires. Combinez les constantes de l'équation en soustrayant 9 des deux côtés du signe égal. Voici comment vous y prendre :
    • 3x + 9 - 9 = 12 - 9
    • 3x = 3
  4. Image intitulée Solve for X Step 15
    4
    Trouvez x en divisant les expressions de chaque côté par le coefficient de x. Pour trouver x, il faut diviser 3x et 9 par 3, le coefficient devant le terme en x. 3x/3 = x et 3/3 = 1, ce qui vous laisse avec x = 1.
  5. Image intitulée Solve for X Step 16
    5
    Vérifiez vos calculs. Pour vérifier que votre travail est bon, réintroduisez la valeur de x dans l'équation d'origine. Voici ce que cela donne :
    • (x + 3)/6 = 2/3
    • (1 + 3)/6 = 2/3
    • 4/6 = 2/3
    • 2/3 = 2/3
    Publicité

Méthode 4
Méthode 4 sur 5:
Équation avec des racines carrées

  1. Image intitulée Solve for X Step 17
    1
    Posez le problème. Imaginons que vous deviez trouver x dans l'exemple suivant [2]  :
    • √(2x+9) - 5 = 0
  2. Image intitulée Solve for X Step 18
    2
    Isolez votre racine. Avant d'aller plus loin, il faut placer la racine d'un côté de l'équation. Cela revient donc à additionner 5 des deux côtés de l'équation. Voici comment faire :
    • √(2x+9) - 5 + 5 = 0 + 5
    • √(2x+9) = 5
  3. Image intitulée Solve for X Step 19
    3
    Élevez l'équation au carré des deux côtés du signe égal. Tout comme vous diviseriez les deux côtés de l'équation par le coefficient du terme en x, vous devez élever au carré les deux côtés de l'équation si x se trouve sous la racine carrée. Vous éliminerez ainsi la racine carrée de l'équation. Voici ce que cela donne :
    • (√(2x+9))2 = 52
    • 2x + 9 = 25
  4. Image intitulée Solve for X Step 20
    4
    Regroupez les termes identiques. Combinez les termes similaires en soustrayant les deux côtés de l'équation par 9, de sorte que toutes les constantes se retrouvent à droite de l'équation tandis que les x restent à gauche. Dans notre cas, voici comment faire :
    • 2x + 9 - 9 = 25 - 9
    • 2x = 16
  5. Image intitulée Solve for X Step 21
    5
    Isolez l'inconnue. La dernière chose à faire pour trouver x consiste à isoler l'inconnue en divisant les deux membres de l'équation par le coefficient de x, soit 2. 2x/2 = x et 16/2 = 8, on a donc x = 8.
  6. Image intitulée Solve for X Step 22
    6
    Vérifiez vos calculs. Remplacez x par 8 dans l'équation x pour voir si vous obtenez le bon résultat :
    • √(2x+9) - 5 = 0
    • √(2(8)+9) - 5 = 0
    • √(16+9) - 5 = 0
    • √(25) - 5 = 0
    • 5 - 5 = 0
    Publicité

Méthode 5
Méthode 5 sur 5:
Équations comprenant une valeur absolue

  1. Image intitulée Solve for X Step 23
    1
    Écrivez le problème. Imaginons que vous ayez à trouver x dans l'exemple suivant [3]  :
    • |4x +2|- 6 = 8
  2. Image intitulée Solve for X Step 24
    2
    Isolez la valeur absolue. La première chose à faire est de regrouper les termes similaires d'un côté de l'équation et de placer l'expression à l'intérieur des symboles de valeur absolue de l'autre côté. Dans notre exemple, cela consiste à ajouter un 6 de chaque côté de l'équation. Voici comment procéder :
    • |4x +2|- 6 = 8
    • |4x +2|- 6 + 6 = 8 + 6
    • |4x +2|= 14
  3. Image intitulée Solve for X Step 25
    3
    Retirez la valeur absolue et résolvez l'équation. C'est la première étape et la plus simple. Lorsque vous travaillez avec des valeurs absolues, vous devez résoudre x deux fois. Voici comment faire la première :
    • 4x + 2 = 14
    • 4x + 2 - 2 = 14 -2
    • 4x = 12
    • x = 3
  4. Image intitulée Solve for X Step 26
    4
    Retirez à nouveau la valeur absolue et n'oubliez pas d'inverser le signe de la constante avant de résoudre la seconde équation. Refaites la même suite de calcul, mais en remplaçant 14 par -14 dans la première ligne de calcul. Cela nous donne :
    • 4x + 2 = -14
    • 4x + 2 - 2 = -14 - 2
    • 4x = -16
    • 4x/4 = -16/4
    • x = -4
  5. Image intitulée Solve for X Step 27
    5
    Vérifiez vos calculs. À présent que vous savez que x = (3, -4), réintroduisez ces valeurs dans l'équation d'origine pour voir si cela fonctionne. Voici comment vous y prendre :
    • (Pour x = 3) :
      • |4x +2|- 6 = 8
      • |4(3) +2|- 6 = 8
      • |12 +2|- 6 = 8
      • |14|- 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    • (Pour x = -4) :
      • |4x +2|- 6 = 8
      • |4(-4) +2|- 6 = 8
      • |-16 +2|- 6 = 8
      • |-14|- 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    Publicité

Conseils

  • Les racines sont une autre façon de représenter les exposants. La racine carrée de x peut aussi s'écrire x1/2.
  • Pour vérifier votre travail, remplacez x par sa valeur dans l'équation initiale puis faites les calculs.
Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des degrés en radians
Comment
convertir des degrés en radians
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://www.decodedscience.com/cross-multiply-to-solve-equations-with-fractions/25496
  2. ↑ http://www.mathsisfun.com/algebra/radical-equations-solving.html
  3. ↑ http://www.sosmath.com/algebra/solve/solve0/solve0.html

À propos de ce wikiHow

David Jia
Coécrit par:
David Jia
Tuteur de mathématiques
Cet article a été coécrit par David Jia. David Jia est tuteur académique et fondateur de LA Math Tutoring, un centre privé de tutorat situé à Los Angeles, en Californie. Il a plus de 10 ans d'expérience dans l'enseignement, et il travaille avec des étudiants de tous âges et de tous niveaux dans diverses matières, ainsi qu'avec des conseillers en admission à l'université et en préparation aux tests SAT, ACT, ISEE, etc. Après avoir obtenu une note parfaite de 800 en mathématiques et de 690 en anglais au SAT, David a reçu la bourse Dickinson de l'université de Miami, où il a obtenu une licence en administration des affaires. En outre, David a travaillé comme instructeur afin de réaliser des vidéos en ligne pour des sociétés spécialisées dans les manuels scolaires comme Larson Texts, Big Ideas Learning et Big Ideas Math. Cet article a été consulté 101 906 fois.
Catégories: Mathématiques
Publicité