Comment calculer une racine carrée sans calculatrice

Informations concernant l'auteur.e

En mathématiques, des nombres peuvent être liés entre eux par une relation particulière, il est ainsi de ce qu'on appelle la racine carrée et le carré. Quand vous multipliez un nombre par lui même, vous obtenez son carré et quand vous prenez la racine carrée de ce carré, vous obtenez le nombre de départ. Avec les calculatrices, ces deux calculs, élévation au carré et racine carrée, sont d'une simplicité enfantine. L'extraction de la racine est cependant possible avec une feuille de papier, un crayon et les quatre opérations élémentaires (addition, soustraction, multiplication et division).

Méthode 1

Méthode 1 sur 4:
Savoir ce qu'est une racine carrée

1
Soyez prudent avec une racine carrée. ${\sqrt {a}}$ ${\sqrt {a}}$ (à lire « racine de a ») correspond au nombre dont le carré vaut $a$ $a$ : $({\sqrt {a}})^{2}=a$ $({\sqrt {a}})^{2}=a$ . Comme un carré est toujours positif, les nombres négatifs n'ont pas de racine. La racine d'un nombre peut être un entier et c'est le cas des carrés parfaits : 16 est un carré parfait et sa racine est 4. Mais elle peut aussi être un nombre décimal, comme
${\sqrt {20,25}}=4,5$ ${\sqrt {20,25}}=4,5$ . Dernier cas : certaines racines sont dites « irrationnelles », comme ${\sqrt {2}}=1,414213...$ ${\sqrt {2}}=1,414213...$
- Connaissez la terminologie. Une racine est notée ${\sqrt {}}$ (le radical) et la valeur qui se trouve en dessous est le radicande.
2
Retenez qu'une racine est donc toujours positive ou nulle. Cependant, dans les équations, il en va un peu différemment. Si l'on prend l'équation
$x={\sqrt {25}}$ , $x$ a deux valeurs possibles : $x=5$ ou $x=-5$ . Ces deux valeurs élevées au carré donnent également 25 ^{[1]
X
Source de recherche}.

Publicité

Méthode 2

Méthode 2 sur 4:
Calculer une racine carrée par encadrements successifs

1
Trouvez les deux nombres encadrants ^{[2]
X
Source de recherche}. Après avoir regardé votre nombre, trouvez deux nombres simples dont les carrés encadrent votre nombre de départ, dont vous cherchez la racine. Comme le travail se fait à la main, prenez des centaines, des milliers…
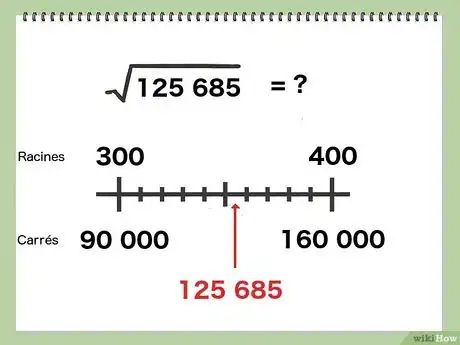
- Exemple : vous devez trouver la racine de 125 685. Encadrez cette valeur par deux valeurs qui sont des carrés. Si vous prenez 10 000 (carré de 100) et
  40 000 (carré de 20), vous voyez que vous êtes loin du compte. Par contre, si vous prenez les carrés de 300 (90 000) et 400 (160 000), vous y êtes :
  $90\ 000<125\ 685<160\ 000$ . La racine que vous cherchez est comprise entre 300 et 400 : ce n'est déjà pas si mal !
2
Affinez votre résultat. Bien évidemment, une approximation ne peut pas être une réponse, il faut donc l'affiner. Faites la différence entre votre nombre et la valeur la plus basse, puis entre la valeur la plus haute et votre nombre. Voyez où se situe entre ces deux valeurs extrêmes votre nombre.
- Calculez $125\ 685-90\ 000=35\ 685$ , puis $160\ 000-125\ 685=34\ 315$ . Les deux différences sont très proches, donc la racine de votre nombre doit se situer au milieu de l'intervalle 300-400, vers 350 donc !
3
Trouvez deux nombres plus précis. En fonction de ce que vous avez observé, faites un autre essai avec deux valeurs plus précises.
- Nous savons que la réponse se situe vers 350. Aussi, allez-vous encadrer avec 350 et 360, vous auriez aussi pu prendre 340 et 350, mais la différence de droite est inférieure à celle de gauche, donc la réponse est supérieure à 350. Vous obtenez donc l'encadrement suivant : $122\ 500<125\ 685<129\ 600$ ! La solution n'est pas loin, non ?
4
Affinez encore votre résultat. Vous procédez de la même façon en fonction de l'encadrement obtenu. Voyez bien les écarts et resserrez votre encadrement autant de fois que nécessaire pour obtenir la précision voulue.
- La réponse est entre 350 et 360 et au vu du dernier encadrement, il semblerait que la réponse soit vers 355, mais juste inférieure. En effet, si vous encadrez votre nombre entre les carrés de 354 et 355, vous tombez juste :
  $125\ 316<125\ 685<126\ 025$ . Vous pouvez continuer aussi longtemps que vous voulez, en prenant même des nombres décimaux. La solution ici était :
  ${\sqrt {125685}}\approx 354,520$ .
Publicité

Méthode 3

Méthode 3 sur 4:
Calculer le carré avec une fausse division

1
Séparez les chiffres de votre nombre par groupe de deux. Vous commencez par la droite en dissociant votre nombre par groupes de deux chiffres ^{[3]
X
Source de recherche}.
- Exemple : vous devez trouver la racine de 125 685. Sur votre feuille, inscrivez 12 56 85.
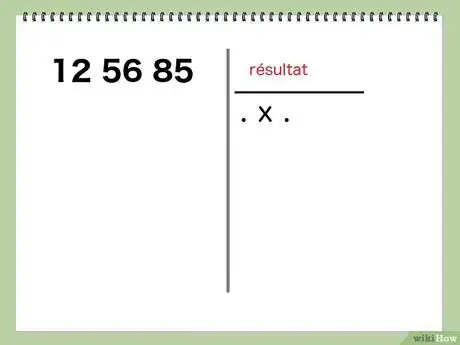
2
Préparez le cadre opératoire. Tracez une barre verticale et une autre horizontale, à l'image d'une division classique. Sous la barre de droite, inscrivez la mention suivante : . x .. Au fil des opérations, le résultat (la racine carrée) apparaitra sur la droite et au-dessus de la barre, là où est habituellement le diviseur.
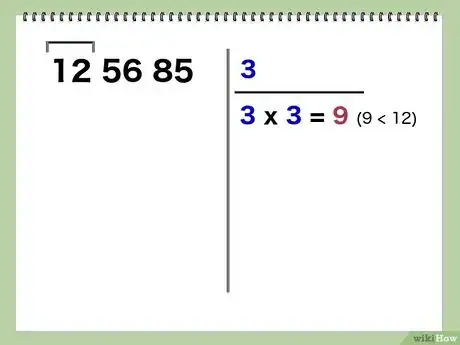
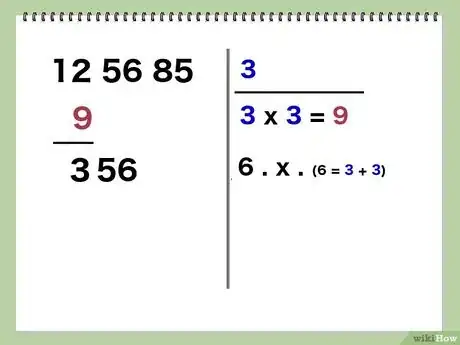
3
Envisagez le premier groupe de deux chiffres. Vous devez inscrire à droite la multiplication d'un seul et même chiffre (remplaçant les deux points) dont le résultat est le plus proche de la tranche de gauche. Ce chiffre sera le premier de la racine et sera placé au-dessus du trait de division.
- Exemple : si vous remplacez le point par 4, vous obtenez : 4 x 4 = 16, résultat supérieur à 12, donc il faut prendre 3, car : 3 x 3 = 9, inférieure à 12. Inscrivez 3 au-dessus de la barre de division.
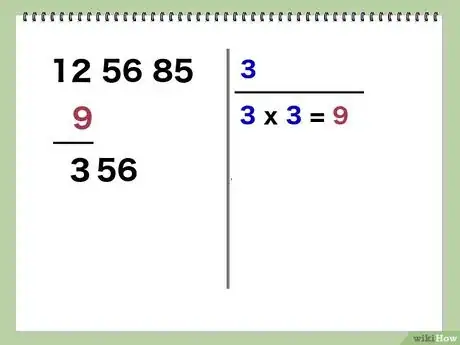
4
Inscrivez le reste, puis abaissez la tranche suivante. Cela ressemble quand même à une division. Vous allez ôter de tête le résultat de la multiplication de la première tranche et inscrire le reste sous le second chiffre de la première tranche. Enfin, vous abaissez la deuxième tranche.
- Exemple : vous ôtez 9 de 12 et il vous reste 3 que vous inscrivez sous le 2 de 12. Abaissez la tranche 56, ce qui vous donne 356.
5
Additionnez les opérandes de la multiplication. Faites la somme des deux chiffres de la multiplication précédente, puis inscrivez le résultat sous la multiplication précédente en ajoutant deux points et le signe $\times$ $\times$ .
- Exemple : faites 3 + 3 = 6, puis inscrivez à droite 6 . x . Alignez cette opération avec le nombre de gauche. Vous le voyez, on retombe sur le principe de départ.
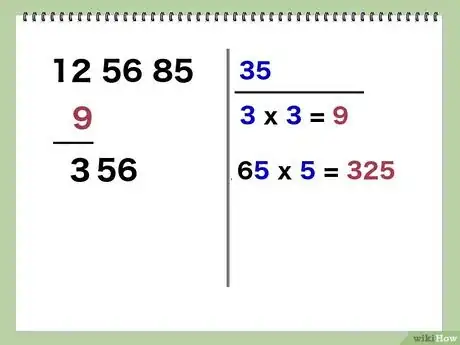
6
Trouvez le deuxième chiffre de la racine. Vous devez trouver un seul et même chiffre qui devra donner comme résultat un nombre inférieur à celui de gauche, mais le plus proche possible. Ce chiffre sera le deuxième chiffre de la racine.
- Exemple : ici, ce chiffre est 5, car 65 x 5 = 325 (6 donnerait un résultat trop élevé). Inscrivez ce chiffre à droite du premier chiffre de la racine (35).
7
Trouvez les autres chiffres de la racine. Vous avez à présent compris le système : vous faites la somme des opérandes, vous cherchez un chiffre qui donne un résultat de multiplication inférieur au nombre de gauche et vous l'inscrivez à la suite des chiffres déjà trouvés de la solution.
- Si vous voulez un résultat plus précis, avec une virgule, arrivé(e) au bout de votre chiffre, abaissez un 00 et mettez une virgule dans la solution, puis continuez comme cela a été expliqué ici.
- Dans notre exemple, pour obtenir la solution à une décimale, nous avons abaissé 00 et avons trouvé que : ${\sqrt {125685}}\approx 354,5$ . Ce résultat n'est qu'une valeur approchée, il faudrait continuer à trouver les autres décimales.
- Quand vous tombez sur un reste égal à 0, alors, vous obtenez une réponse exacte. Si celle-ci n'a pas de virgule, le nombre de départ était un carré parfait, comme 16 (carré de 4) ou 12 321 (carré de 111).
Publicité

Méthode 4

Méthode 4 sur 4:
Calculer une racine carrée par appel des impairs

1
Retenez cette propriété étonnante des carrés. Le carré d'un nombre ( $n$ $n$ ) est égal à la somme des n premiers nombres impairs. Mathématiquement, cela se traduit par la formule : $n^{2}=\sum \limits _{i=1}^{2n-1}{n}=1+(2+1)+(4+1)...$ $n^{2}=\sum \limits _{i=1}^{2n-1}{n}=1+(2+1)+(4+1)...$
- À titre d'exemple, $7^{2}=1+3+5+7+9+11+13=49$ . C'est la somme des 7 premiers nombres impairs.
- Cette méthode ne fonctionne qu'avec des radicandes entiers.
2
Trouvez le premier chiffre de la solution. Établissez la somme des impairs équivalant à votre nombre, au moins les premiers termes. Voyez combien il vous faut de termes pour obtenir un résultat égal ou inférieur à votre nombre de départ.
- Exemple : on vous demande de trouver la racine carrée de 46. Sa décomposition en somme des entiers impairs commence ainsi :
  46 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17… Pour obtenir 46 ou moins, vous devez utiliser les 6 premiers termes (1 + 3 + 5 + 7 + 9 + 11 = 36). La racine de 46 commence donc par un 6 et il vous reste 10. Mettez immédiatement une virgule après ce 6.
3
Trouvez le second chiffre de la racine. Ajoutez la tranche 00 au reste, récupérez le dernier nombre de la somme, ajoutez-lui 1, multipliez le tout par 10 et ajoutez 1 à ce résultat. Retirez ce dernier résultat du reste augmenté de 00. Si de ce reste vous pouvez encore retirer un ou plusieurs autres impairs consécutifs, faites-le jusqu'à ne plus y arriver. Le nombre d'impairs utilisés est alors votre deuxième chiffre de la racine.
- Si le nombre que vous devez retirer du nombre se terminant par 00 est supérieur à ce dernier nombre, alors le deuxième chiffre est 0. Vous gardez ce reste et le comparez cette fois au reste encore augmenté de 00 et gardez le même reste… et ses suivants. Essayez avec ${\sqrt {26}}$ !
- Dans notre exemple, il restait 10 qui se voit flanqué de la tranche 00, soit 1 000. Le dernier de la somme était 11, auquel on ajoute 1 (12) que l'on multiplie par 10 (120) et auquel on ajoute 1, soit 121. Ce nombre est alors retiré de 1 000, soit 879. Nous avons retiré 121 et nous pouvons retirer l'impair suivant, soit 123, ce qui donne : 879 - 123 = 756. 125 peut aussi être retiré, soit : 756 - 125 = 631 ; 127 aussi (504), 129 également (375), 131 aussi (244) et enfin 133 (111). Dans cette opération, nous avons utilisé 7 nombres impairs (de 121 à 133) : 7 est le deuxième chiffre de la racine.
4
Trouvez les autres chiffres de la racine. Le principe est le même : ajoutez la tranche 00 au reste précédent, ajoutez 1, multipliez par 10 et ajoutez 1. Retirez ce dernier résultat du reste multiplié précédemment par 100. Si de ce reste vous pouvez encore retirer un plusieurs autres impairs consécutifs, faites-le jusqu'à ne plus y arriver. Le nombre d'impairs utilisés est alors votre deuxième chiffre de la racine.
- Si, à n'importe quel stade, votre reste est 0, alors les calculs sont terminés.
- Dans notre exemple, il restait 111 qui se voit flanqué de la tranche 00, soit 111 000. Le dernier de la somme était 133, auquel on ajoute 1 (134) que l'on multiplie par 10 (1 340) et auquel l'on ajoute 1, soit 1 341. Ce nombre est alors retiré de 111 000, soit 109 659. Il est possible de retirer les 7 impairs consécutifs, ce qui fait au total 8 nombres impairs (de 1 341 à 1 348) : 8 est le troisième chiffre de la racine.
5
Présentez correctement votre résultat. Il est évident que plus le radicande est élevé, plus grands sont les risques d'erreurs. Soyez vigilant(e) !
- Dans notre exemple, après tous ces calculs, vous pouvez écrire, si 2 décimales sont exigées, la solution suivante : ${\sqrt {46}}\approx 6,78$ .
Publicité

Avertissements

Le calcul d'une racine ne doit jamais déboucher sur une valeur négative. Elle est toujours supérieure ou égale à 0.
Si ${\sqrt {-a}}$ n'existe pas, $-{\sqrt {a}}$ existe par contre. Plus tard peut-être, vous tomberez sur une égalité étrange : $i^{2}=-1$ . Vous êtes dans les nombres complexes et la racine d'un nombre complexe peut être calculée, mais c'est… complexe ^{[4]
X
Source de recherche} !