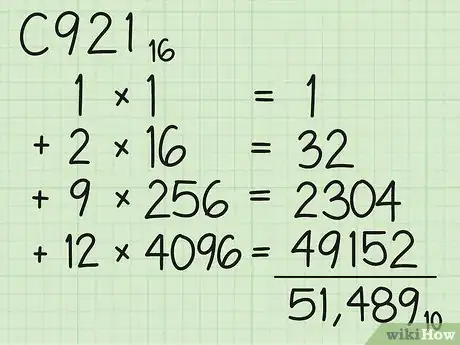Comment convertir un nombre hexadécimal en nombre binaire ou en nombre décimal

Informations concernant l'auteur.e

Le système de numération hexadécimale est très original, car outre les chiffres, il utilise des lettres, ce qui est déroutant pour nous. Il est possible de passer d’un système à l’autre. Ainsi, convertir des nombres hexadécimaux en nombres binaires est assez simple, ce qui explique qu'ils sont souvent utilisés dans les langages de programmation. La conversion des nombres hexadécimaux en nombres décimaux est plus compliquée, mais, avec un peu de pratique, elle est aisée.

Partie 1

Partie 1 sur 3:
Convertir un nombre hexadécimal en nombre binaire

1

Passez de l’hexadécimal au binaire. Chaque chiffre hexadécimal se transforme en quatre chiffres binaires. C’est pourquoi on passe facilement de la notation binaire à la notation hexadécimale. En fait, l’avantage de cette dernière est qu’elle permet d’écrire de façon plus courte des nombres binaires extrêmement longs. Avec le tableau ci-dessous, vous convertirez facilement de la base seize à la base deux.

Hexadécimal	Binaire
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

2
Essayez pour voir. Il est très facile de transformer un caractère hexadécimal en quatre caractères binaires… à condition d’avoir le tableau de conversion. Voici quelques exercices pour vous faire la main. Pour voir la réponse des exemples ci-dessous, sélectionnez l’espace apparemment vide à droite du signe « = » :
- A23 = 1010 0010 0011
- BEE = 1011 1110 1110
- 70C558 = 0111 0000 1100 0101 0101 1000
3
Comprenez comme se fait la conversion. En notation binaire, en base 2, on utilise que deux caractères (0 et 1) pour écrire tous les nombres. Ainsi, avec 4 caractères, vous pouvez écrire 2⁴ = 16 nombres décimaux différents. La notation hexadécimale étant une notation en base seize, avec un caractère vous pouvez écrire 16¹ = 16 nombres décimaux différents. C’est la raison pour laquelle la conversion entre les deux bases est aussi facile.
- Dans les deux systèmes de numération, le changement de rang évolue simultanément. En numération hexadécimale, on a la suite « … D, E, F, 10 » et en binaire, on a la suite « … 1101, 1110, 1111, 10000 ».
Publicité

Partie 2

Partie 2 sur 3:
Convertir un nombre hexadécimal en nombre décimal

1
Révisez les principes de la base dix. La notation décimale est aujourd’hui notre système de comptage et on n’y pense plus, mais, souvenez-vous, quand vous étiez enfant, il vous a fallu l’apprendre avec vos parents et vos professeurs. Un petit rappel du fonctionnement de cette notation n’est peut-être pas inutile pour faire des conversions.
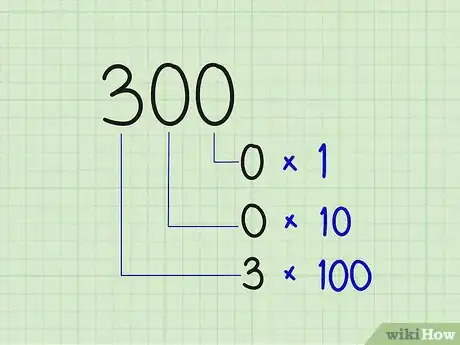
- En notation décimale, chaque chiffre d’un nombre a une place et une valeur bien déterminées. De droite à gauche, on a les unités, les dizaines, les centaines… Ainsi le chiffre 3 placé en unité vaut 3, placé en dizaine, il vaut 30 et placé en centaine, il vaut 300.
- Mathématiquement, les unités représentent 10⁰, les dizaines, 10¹, les centaines, 10²… Ce sont ces puissances de dix qui ont donné son nom à la notation (en latin, « decimus » signifie « dix »).
2
Sachez qu’un nombre décimal est le résultat d'une addition. C’est peut-être une évidence, mais c’est cette propriété que l’on utilise pour convertir un nombre hexadécimal. Pour l’exemple, décomposons le nombre 480 137₁₀, l’indice ₁₀ rappelle ici que le nombre est formulé en base dix.
- Commencez par le dernier chiffre, le plus à droite, 7 = 7 x 10⁰, soit 7 x 1
- Passez au chiffre suivant : 3 = 3 x 10¹, soit 3 x 10
- Continuez ainsi avec les autres chiffres. Pour résumer, vous obtenez alors : 480 137 = (4 x 100 000) + (8 x 10 000) + (0 x 1 000) + (1 x 100) + (3 x 10) + (7 x 1)
3
Attribuez à chaque caractère la puissance qui lui correspond. Un nombre hexadécimal étant en base seize, c’est la place du caractère dans le nombre qui va déterminer la puissance de seize. Pour convertir en système décimal, multipliez chaque caractère (chiffre ou lettre) par la puissance de seize correspondante. Vous devez donc récrire chaque caractère du nombre hexadécimal flanqué d’une puissance de seize. Nous allons convertir en nombre décimal le nombre C921₁₆. Commencez par le caractère de droite (1) qu’on multiplie toujours par 16⁰. Passez au caractère suivant, à gauche, et multipliez-le par la puissance de seize suivante (16¹). On a ainsi :
- 1₁₆ = 1 x 16⁰ = 1 x 1 (tous les nombres sans indice sont en notation décimale)
- 2₁₆ = 2 x 16¹ = 2 x 16
- 9₁₆ = 9 x 16² = 9 x 256
- C = C x 16³ = C x 4 096
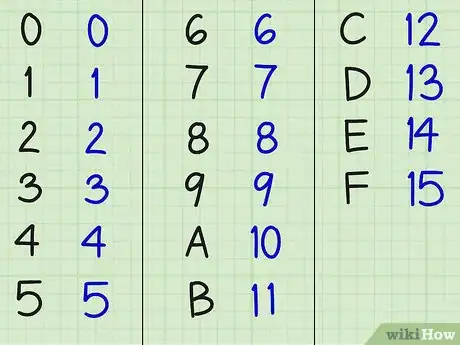
4
Convertissez les caractères alphabétiques. Les chiffres sont les mêmes en base seize et en base dix, la conversion est dès lors inutile, car évidente : par exemple, 7₁₆ = 7₁₀). Quant aux lettres de la base seize, servez-vous de la liste ci-dessous pour la conversion en base dix :
- A = 10
- B = 11
- C = 12 (c’est la lettre que l’on a dans l’exemple précédent)
- D = 13
- E = 14
- F = 15
5
Faites les calculs. Maintenant que tout a été transformé en système décimal, il ne reste plus qu’à faire les multiplications, puis l’addition. Certes, on peut calculer à la main, mais une calculatrice s’avère souvent utile avec les nombres hexadécimaux. Reprenons l’exemple précédent, à savoir C921 qu’on veut convertir en base dix. On a donc à calculer cette somme de produits :
- C921₁₆ = (1 x 1) + (2 x 16) + (9 x 256) + (12 x 4 096)
- = 1 + 32 + 2 304 + 49 152
- = 51 489₁₀. Comme vous le voyez, le nombre décimal contient plus de chiffres qu’en notation hexadécimale. C’est assez logique dans la mesure où la référence est seize, et non pas dix. Un nombre binaire est très long, un même nombre en base 60 est court.
6
Exercez-vous à convertir. Voici cinq exemples de conversion, de l’hexadécimal vers le décimal, pour voir si vous avez compris. Posez les opérations, puis faites les calculs. Une fois le résultat obtenu, regardez la réponse en sélectionnant l’espace apparemment vide à droite du signe « = ».
- 3AB₁₆ = 939₁₀
- A1A1₁₆ = 41377₁₀
- 5000₁₆ = 20480₁₀
- 500D₁₆ = 20493₁₀
- 18A2F₁₆ = 100911₁₀
Publicité

Partie 3

Partie 3 sur 3:
Comprendre les bases de la notation hexadécimale

1

Sachez comment fonctionne la notation hexadécimale. La notation décimale qu’on utilise tous les jours est en base 10, c’est-à-dire qu’on utilise dix chiffres pour écrire tous les nombres. Quant au système hexadécimal, il est en base seize, c’est-à-dire qu’on utilise seize caractères pour écrire tous les nombres.

Voici l’écriture des 32 premiers nombres décimaux en base seize :

Hexadecimal	Decimal	Hexadecimal	Decimal
0	0	10	16
1	1	11	17
2	2	12	18
3	3	13	19
4	4	14	20
5	5	15	21
6	6	16	22
7	7	17	23
8	8	18	24
9	9	19	25
A	10	1A	26
B	11	1B	27
C	12	1C	28
D	13	1D	29
E	14	1E	30
F	15	1F	31

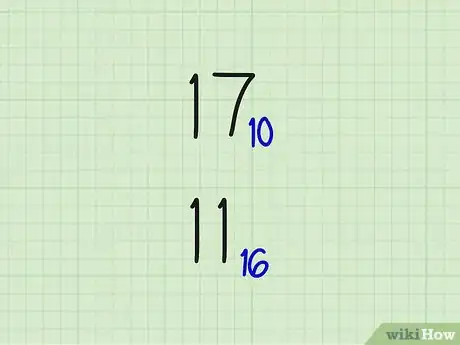
2
Notez l’indice de la base. Si vous travaillez avec plusieurs bases, inscrivez toujours en indice la base utilisée, cette dernière est une valeur décimale. Ainsi, 17₁₀ se lit « 17 en base dix » (c’est le nombre 17 que nous connaissons tous). Par contre, 17₁₀ s’écrit 11₁₆, qui se lit « 11 en base seize » (hexadécimal). Si votre nombre contient une lettre (A, B, C…), il est inutile de préciser la base, car personne ne pourra le confondre avec une valeur décimale.

Publicité

Conseils

Pour convertir de grands nombres hexadécimaux en base dix, vous pouvez utiliser une calculatrice en ligne à convertir. Plus pratique, utilisez un convertisseur de base à base. Si vous utilisez ce dernier, vous irez plus vite, mais vous ne comprendrez pas les mécanismes de conversion ^{[1]
X
Source de recherche}.
Vous venez de voir comment on convertit des nombres hexadécimaux en nombres décimaux. Il est possible de faire de même depuis des nombres en base $x$ vers la base dix. Remplacez simplement les puissances de seize par des puissances de $x$ . Pour vous amuser, essayez de comprendre le système babylonien en base… 60 ^{[2]
X
Source de recherche} : bonne chance !