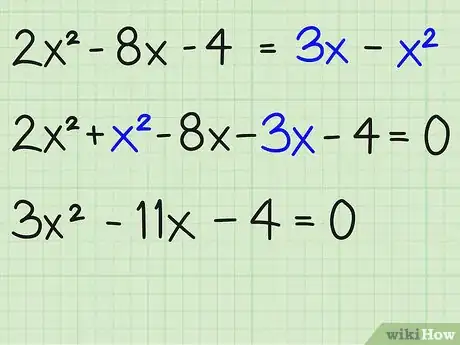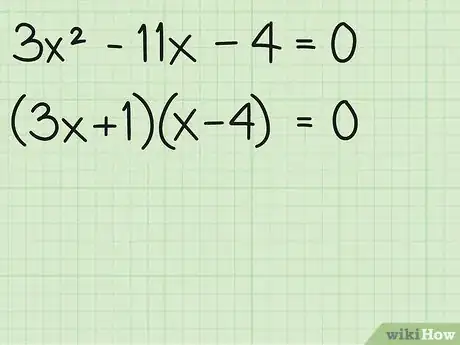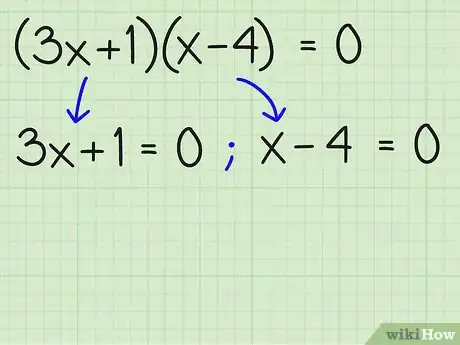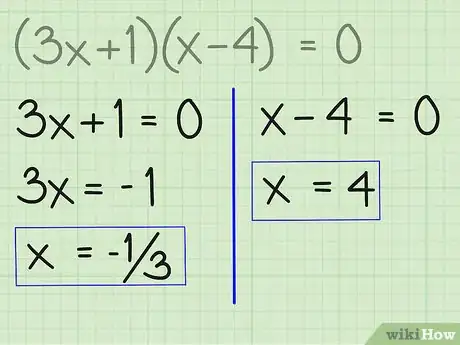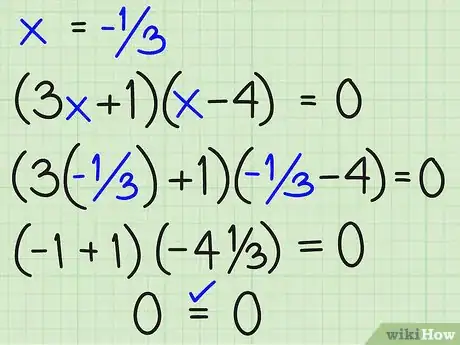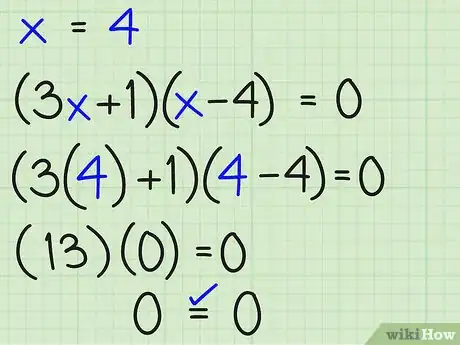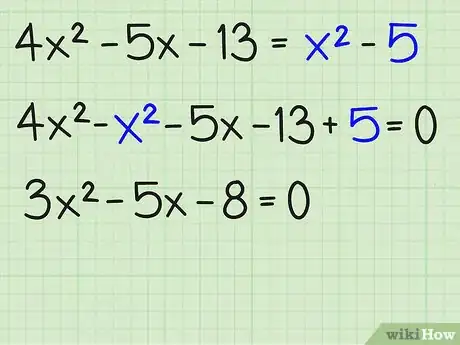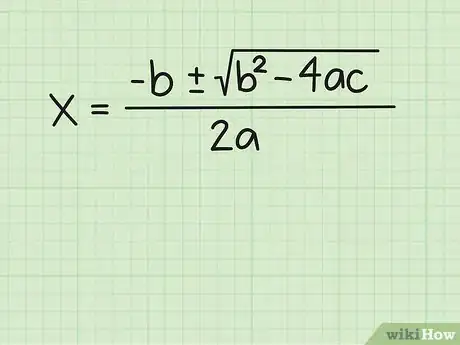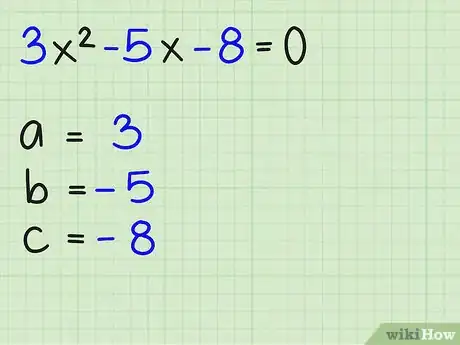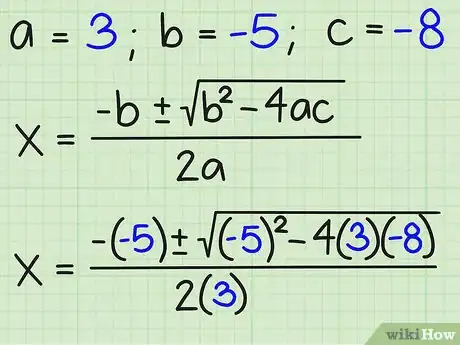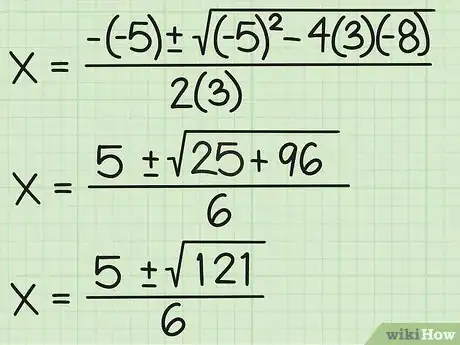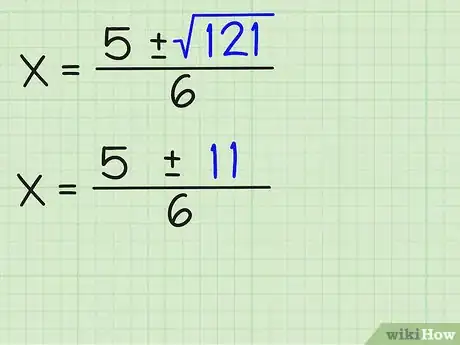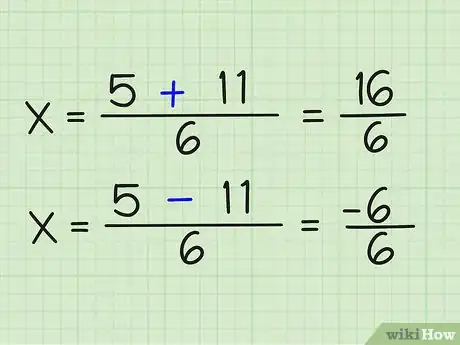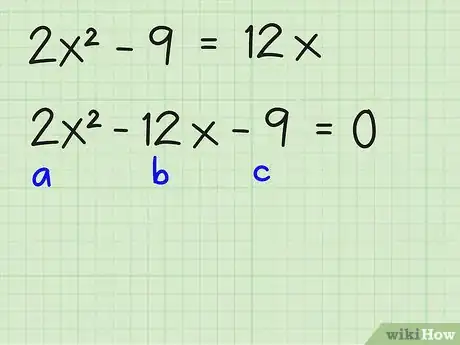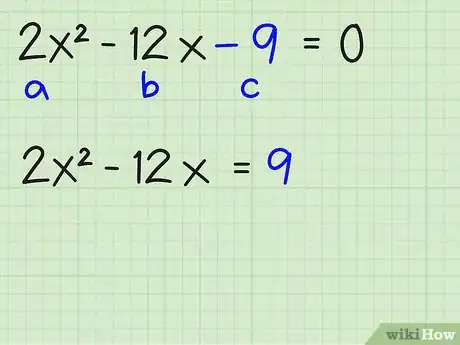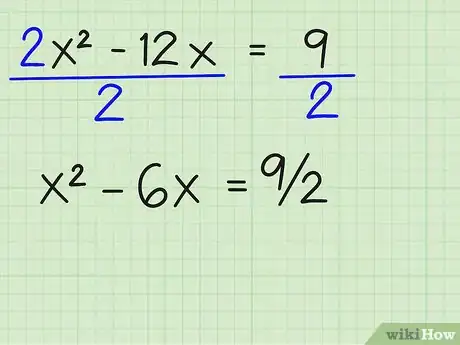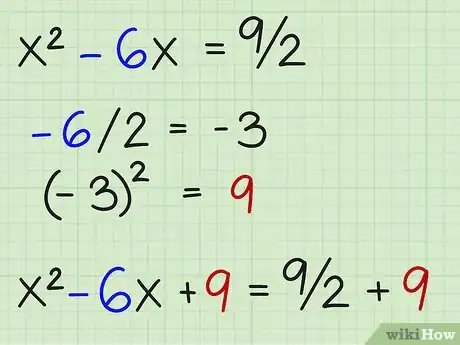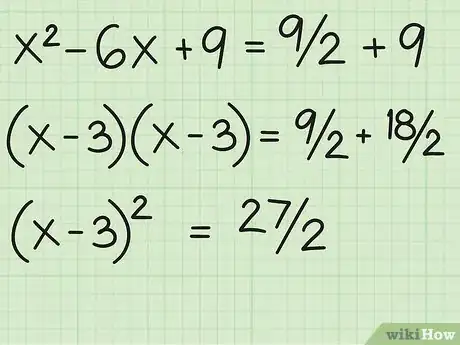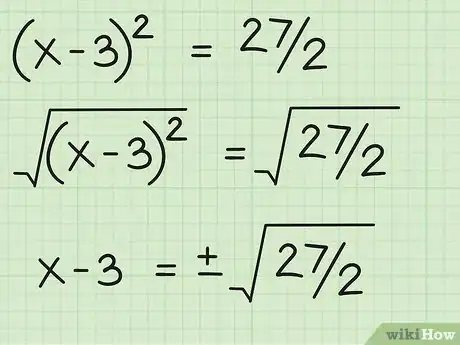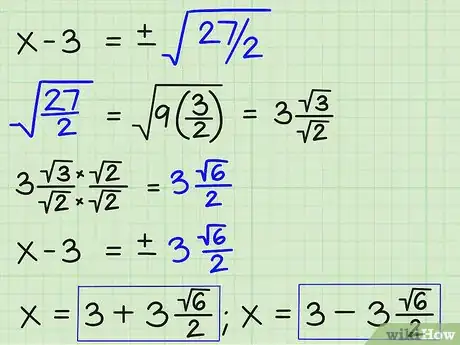Comment résoudre une équation du second degré

Coécrit par David Jia

Une équation du second degré est un type d'équation mathématique où la plus grande puissance de x (soit le degré de l'équation) vaut 2. Il est possible de résoudre une équation du second degré de trois façons différentes : en factorisant l'équation si c'est possible, en utilisant la formule quadratique ou en élevant au carré.

Méthode 1
Méthode 1 sur 3:
Factoriser l'équation

  1. Image intitulée Solve Quadratic Equations Step 1
    1
    Combinez tous les termes similaires et placez-les d'un seul côté de l'équation. La première étape consiste à déplacer tous les termes similaires du même côté de l'équation, en faisant en sorte que le terme en x2 reste positif. Pour combiner tous les termes, additionnez ou soustrayez tous les termes en x2, les termes en x ainsi que les constantes (soit les nombres entiers), puis déplacez-les d'un côté de l'équation pour que rien ne reste de l'autre côté. Une fois que vous aurez terminé cette étape, ajoutez un "0" du côté de l'équation où il n'y a rien. Voici comment vous y prendre [1]  :
    • 2x2 - 8x - 4 = 3x - x2 =
    • 2x2 +x2 - 8x -3x - 4 = 0
    • 3x2 - 11x - 4 = 0
  2. Image intitulée Solve Quadratic Equations Step 2
    2
    Factorisez l'expression. Pour factoriser l'expression, vous devez utiliser les facteurs du terme en x2 (soit le coefficient égal à 3), ainsi que les facteurs de la constante (-4) pour qu'ils se multiplient et s'additionnent de sorte à obtenir le coefficient du terme en x (-11). Voici comment faire.
    • Puisque 3x2 ne possède qu'un seul ensemble de facteurs, soit 3x et x, vous pouvez écrire ces facteurs entre parenthèses : (3x +/- ? )(x +/- ?) = 0.
    • Ensuite, procédez par élimination pour introduire les facteurs de 4 de sorte à trouver une combinaison qui donne -11x après multiplication. Vous pouvez utiliser une combinaison de 4 et 1, ou de 2 et 2, puisque ces deux combinaisons de chiffres donnent un 4 après multiplication. Rappelez-vous toutefois que l'un de ces termes doit être négatif, puisque la valeur recherchée est de -4.
    • Essayez avec (3x +1)(x -4). Lorsque vous multipliez ces deux expressions, vous obtenez - 3x2 -12x +x -4. Si vous combinez les termes -12x et x, vous obtenez alors -11x, qui est le terme en x que vous cherchiez. Vous venez tout juste de factoriser l'équation du second degré.
    • Par exemple, essayons de factoriser des combinaisons qui ne fonctionnent pas : (3x -2)(x +2) = 3x2 +6x -2x -4. Si vous combinez ces termes, vous obtiendrez 3x2 -4x -4. Si la multiplication des facteurs -2 et 2 donne -4, vous n'obtiendrez pas le terme voulu qui est égal à -11x.
  3. Image intitulée Solve Quadratic Equations Step 3
    3
    Posez chaque expression entre parenthèses égale à zéro. De cette façon, vous pourrez trouver les deux valeurs de x pour lesquelles la totalité de l'équation est égale à zéro. À présent que vous avez factorisé l'équation, tout ce que vous avez à faire est de poser chaque expression entre parenthèse comme égale à zéro. Vous devrez donc écrire 3x +1 = 0 et x - 4 = 0.
  4. Image intitulée Solve Quadratic Equations Step 4
    4
    Résolvez chaque équation séparément. Dans le cas d'une équation du second degré, vous obtiendrez deux valeurs de x différentes. Résolvez chaque équation indépendamment en isolant la variable, puis écrivez les deux solutions de x. Voici comment vous y prendre :
    • 3x + 1 = 0
      • 3x = -1
      • 3x/3 = -1/3
      • x = -1/3
    • x - 4 = 0
      • x = 4
    • x = (-1/3, 4)
  5. Image intitulée Solve Quadratic Equations Step 5
    5
    Vérifiez x = -1/3 in (3x + 1)(x – 4) = 0: Nous avons(3[-1/3] + 1)([-1/3] – 4) ?=? 0, mais en subtituant(-1 + 1)(-4 1/3) ?=? 0 par (0)(-4 1/3) = 0 (simplifié) et en multipliant 0 = 0... x = -1/3 fonctionne.
  6. Image intitulée Solve Quadratic Equations Step 6
    6
    Vérifiez x = 4 in (3x + 1)(x - 4) = 0: Nous avons (3[4] + 1)([4] – 4) ?=? 0, en substituant (13)(4 – 4) ?=? 0 par (13)(0) = 0 en multipliant 0 = 0... x = 4 fonctionne.
    • Les deux solutions se vérifient séparément et elles fonctionnent et son correctes avec les deux solutions.
    Publicité

Méthode 2
Méthode 2 sur 3:
Se servir de la formule quadratique

  1. Image intitulée Solve Quadratic Equations Step 7
    1
    Combinez tous les termes similaires et placez-les d'un seul côté de l'équation. Déplacez tous les termes du même côté du signe égal, en faisant en sorte que le terme en x2 soit positif. Écrivez les termes par ordre de puissance décroissante, de sorte que le terme en x2 soit écrit en premier, suivi par le terme en x puis par la constante. Voici comment vous y prendre :
    • 4x2 - 5x - 13 = x2 -5
    • 4x2 - x2 - 5x - 13 + 5 = 0
    • 3x2 - 5x - 8 = 0
  2. Image intitulée Solve Quadratic Equations Step 8
    2
    Écrivez votre formule quadratique. L'équation du second degré peut s'écrire sous la forme : {-b +/-√ (b2 - 4ac)}/2a [2] .
  3. Image intitulée Solve Quadratic Equations Step 9
    3
    Identifiez les valeurs de a, b et c dans l'équation. La variable a est le coefficient du terme en x2, b est celui du terme en x et c est la constante. Dans l'équation 3x2 -5x - 8 = 0, a = 3, b = -5 et c = -8. Écrivez-le.
  4. Image intitulée Solve Quadratic Equations Step 10
    4
    Remplacez les valeurs de a, b et c dans l'équation. À présent que vous connaissez les valeurs de vos trois coefficients, vous pouvez les introduire dans l'équation de la façon suivante :
    • {-b +/-√ (b2 - 4ac)}/2 =
    • {-(-5) +/-√ ((-5)2 - 4(3)(-8))}/2(3) =
    • {-(-5) +/-√ ((-5)2 - (-96))}/2(3)
  5. Image intitulée Solve Quadratic Equations Step 11
    5
    Faites les calculs. Après avoir introduit les chiffres, faites les calculs restants pour simplifier les signes positifs ou négatifs, pour multiplier ou mettre au carré les termes restants. Voici comment faire :
    • {-(-5) +/-√ ((-5)2 - (-96))}/2(3) =
    • {5 +/-√(25 + 95)}/6 =
    • {5 +/-√(120)}/6
  6. Image intitulée Solve Quadratic Equations Step 12
    6
    Simplifiez la racine carrée. Si le nombre sous le radical est un carré parfait, vous obtiendrez un nombre entier. Si le nombre sous la racine n'est pas un carré parfait, essayez de le simplifier au maximum. Si ce nombre est négatif, et que vous en êtes certain(e) alors vous obtiendrez une racine complexe. Dans notre exemple, √(121) = 11. Vous pouvez alors écrire votre résultat de la façon suivante : x = (5 +/- 11)/6.
  7. Image intitulée Solve Quadratic Equations Step 13
    7
    Résolvez les réponses selon que votre racine donne une valeur positive ou négative. Si vous avez éliminé la racine carrée, alors vous pouvez continuer pour trouver votre résultat final selon que le résultat de la racine soit positif ou négatif. À présent que vous avez obtenu (5 +/- 11)/6, vous obtiendrez deux résultats :
    • (5 + 11)/6
    • (5 - 11)/6
  8. Image intitulée Solve Quadratic Equations Step 14
    8
    Résolvez les réponses selon que votre racine donne une valeur positive ou négative. Faites simplement les calculs :
    • (5 + 11)/6 = 16/6
    • (5-11)/6 = -6/6
  9. Image intitulée Solve Quadratic Equations Step 15
    9
    Simplifiez votre résultat. Pour simplifier chaque réponse, il vous suffit de les diviser par le plus grand nombre dont le numérateur et le dénominateur sont tous les deux des multiples. Divisez la première fraction par 2, et la seconde par 6, et vous obtiendrez vos x.
    • 16/6 = 8/3
    • -6/6 = -1
    • x = (-1, 8/3)
    Publicité

Méthode 3
Méthode 3 sur 3:
Élever au carré

  1. Image intitulée Solve Quadratic Equations Step 16
    1
    Déplacez tous les termes du même côté de l'équation. Assurez-vous que le coefficient a devant le x2 est positif. Voici comment faire [3] . :
    • 2x2 - 9 = 12x =
    • 2x2 - 12x - 9 = 0
      • Dans cette équation, le coefficient a vaut 2, le coefficient b vaut -12 et le coefficient c vaut -9.
  2. Image intitulée Solve Quadratic Equations Step 17
    2
    Passez le terme c (soit la constante) de l'autre côté. La constante est le terme numérique sans x. Déplacez-la à droite de l'équation :
    • 2x2 - 12x - 9 = 0
    • 2x2 - 12x = 9
  3. Image intitulée Solve Quadratic Equations Step 18
    3
    Divisez les deux côtés par le coefficient de a ou du terme en x2. Si x2 est exempt de coefficient, ce qui signifie qu'il possède un coefficient égal à 1, alors vous pouvez sauter cette étape. Dans notre cas, il vous faudra diviser tous les termes par 2, de la façon suivante :
    • 2x2/2 - 12x/2 = 9/2
    • x2 - 6x = 9/2
  4. Image intitulée Solve Quadratic Equations Step 19
    4
    Divisez b par 2, élevez la valeur obtenue au carré, et ajoutez le résultat des deux côtés. Dans notre exemple, le coefficient b vaut -6. Voici comment faire :
    • -6/2 = -3 =
    • (-3)2 = 9 =
    • x2 - 6x + 9 = 9/2 + 9
  5. Image intitulée Solve Quadratic Equations Step 20
    5
    Simplifiez les deux côtés. Factorisez le terme du côté gauche pour obtenir (x-3)(x-3), ou (x-3)2. Additionnez les termes du côté droit pour obtenir 9/2 + 9, ou 9/2 + 18/2, ce qui donne 27/2.
  6. Image intitulée Solve Quadratic Equations Step 21
    6
    Trouvez la racine carrée des deux côtés. La racine carrée de (x-3)2 est simplement (x-3). Pour 27/2, vous pouvez écrire : ±√(27/2). Donc, x - 3 = ±√(27/2).
  7. Image intitulée Solve Quadratic Equations Step 22
    7
    Simplifiez la racine pour trouver x. Pour simplifier ±√(27/2), trouvez le carré parfait de 27 ou 2 ou de leurs facteurs. Pour le nombre 27, nous obtenons un carré parfait de 9, car 9 x 3 = 27. Pour extraire le 9 de la racine, enlevez le chiffre 9 et écrivez le chiffre 3, sa racine carrée, à l'extérieur du radical. Ne touchez pas au 3 dans le numérateur sous la racine, car ce facteur de 27 ne peut pas être éliminé, et laissez le chiffre 2 au dénominateur. Puis, déplacez la constante de 3 du côté gauche de l'équation et placez-la à droite, avant de noter vos deux solutions de x :
    • x = 3 +(√6)/2
    • x = 3 - (√6)/2)
    Publicité

Conseils

  • Comme vous pouvez le voir, la solution comporte toujours une racine carrée. En effet le numérateur n’a pu être réduit (car il n'y a pas de terme similaire au dénominateur). Inutile donc de dissocier en deux solutions comportant des plus ou moins. Au lieu de cela, divisez la totalité de l'équation par un facteur commun, mais UNIQUEMENT si ce facteur est bien commun aux deux constantes ET au coefficient de la racine.
  • Si le nombre sous la racine carrée n'est pas un carré parfait, les dernières étapes fonctionneront un peu différemment. Voici un exemple.
  • Si le terme "b" est un nombre pair, cela donnera : {-(b/2) +/- √(b/2)-ac}/a.
Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://www.mathsisfun.com/algebra/factoring-quadratics.html
  2. ↑ http://www.purplemath.com/modules/quadform.htm
  3. ↑ http://www.mathsisfun.com/algebra/completing-square.html

À propos de ce wikiHow

David Jia
Coécrit par:
David Jia
Tuteur académique
Cet article a été coécrit par David Jia. David Jia est tuteur académique et fondateur de LA Math Tutoring, un centre privé de tutorat situé à Los Angeles, en Californie. Il a plus de 10 ans d'expérience dans l'enseignement, et il travaille avec des étudiants de tous âges et de tous niveaux dans diverses matières, ainsi qu'avec des conseillers en admission à l'université et en préparation aux tests SAT, ACT, ISEE, etc. Après avoir obtenu une note parfaite de 800 en mathématiques et de 690 en anglais au SAT, David a reçu la bourse Dickinson de l'université de Miami, où il a obtenu une licence en administration des affaires. En outre, David a travaillé comme instructeur afin de réaliser des vidéos en ligne pour des sociétés spécialisées dans les manuels scolaires comme Larson Texts, Big Ideas Learning et Big Ideas Math. Cet article a été consulté 40 687 fois.
Catégories: Mathématiques
Publicité