معادلة تربيعية

الصيغة التربيعية أو الشكل العام هي العبارة الرياضية التي يتم بها حساب حلول المعادلات التربيعية وتعطى بالعلاقة التالية:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

الرمز "±" يعني وجود حلين هما:

${\displaystyle x_{1}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{,}}\quad x_{2}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$

طريقة استنتاج العلاقة التربيعية

نعتبر معادلة تربيعية من الشكل:

${\displaystyle ax^{2}+bx+c=0\;}$

• يتم قسمة جميع المعامل الأطراف على ${\displaystyle {a}}$ (بما أن ${\displaystyle {a}\neq 0}$):

${\displaystyle {\frac {a}{a}}x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\!}$

• ومنه:

${\displaystyle x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}\!}$

• نضيف عددا يساوي ${\displaystyle ({\frac {b}{2a}})^{2}\!}$ إلى الطرفين وهذا يجعل الطرف الأيسر يبدو في شكل جداء شهير (أو ما يسمى "مربع كامل").

${\displaystyle x^{2}+{\frac {b}{a}}x+({\frac {b}{2a}})^{2}=-{\frac {c}{a}}+({\frac {b}{2a}})^{2}\!}$

• نكتب الطرف الأيسر على شكل جداء تربيعي:

${\displaystyle (x+{\frac {b}{2a}})^{2}={-{\frac {c}{a}}+({\frac {b}{2a}})^{2}}\!}$

• نشكل معادلتين خطيتين بمساواة الجذر التربيعي للطرف الأيسر بالجذر التربيعي الموجب والسالب للطرف الأيمن.

${\displaystyle x+{\frac {b}{2a}}=\pm {\sqrt {-{\frac {c}{a}}+({\frac {b}{2a}})^{2}}}\!}$

• نحل المعادلتين الخطيتين المشكلتين.

${\displaystyle x=-{\frac {b}{2a}}\pm {\sqrt {-{\frac {c}{a}}+({\frac {b}{2a}})^{2}}}\!}$

• بتبسيط العلاقة السابقة نحصل على العبارة التالية والتي تمثل الصيغة التربيعية أوالشكل العام للجذور:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

إذا كان ${\displaystyle \ x_{1}}$ ، ${\displaystyle \ x_{2}}$ هما جذري المعادلة

${\displaystyle ax^{2}+bx+c=0\!}$

فإن العلاقة بين معاملات المعادلة وجذورها تكون كالتالي:

${\displaystyle x_{1}+x_{2}={\frac {-b}{a}}\quad {\text{,}}\quad x_{1}.x_{2}={\frac {c}{a}}}$

يتم استعمال طريقة إكمال المربع بتبسيط المعادلة وتحويلها إلى الشكل: ${\displaystyle x^{2}+2xh+h^{2}=(x+h)^{2}\!}$

ويتم ذلك بإضافة عدد ثابت ذو قيمة مناسبة إلى كلا الطرفين لجعل الطرف الأيسر يظهر في شكل جداء شهير (مربع كامل). ويتم تطبيق الطريقة وفق المراحل التالية: نعتبر معادلة تربيعية من الشكل: ${\displaystyle ax^{2}+bx+c=0\;}$

1. يتم قسمة جميع معاملات الأطراف على ${\displaystyle a}$ (بما أن ${\displaystyle a\neq 0}$)
2. ننقل المعامل الثابت ${\displaystyle {\frac {c}{a}}\!}$ إلى الجانب الآخر للمعادلة (الجانب الأيمن).
3. نضيف عددا يساوي ${\displaystyle ({\frac {b}{2a}})^{2}\!}$ إلى الطرفين وهذا يجعل الطرف الأيسر يبدو في شكل جداء شهير.
4. نكتب الطرف الأيسر على الشكل التربيعي ونبسط الطرف الأيمن إن أمكن.
5. نشكل معادلتين خطيتين بمساواة الجذر التربيعي للطرف الأيسر بالجذر التربيعي الموجب والسالب للطرف الأيمن.
6. نحل المعادلين الخطتين المشكلتين.

مثال توضيحي

إيجاد حلول المعادلة: ${\displaystyle x^{2}+2x-2=0\!}$

${\displaystyle x^{2}+2x-2=0\!}$
${\displaystyle x^{2}+2x=2\!}$
${\displaystyle x^{2}+2x+1=2+1\!}$
${\displaystyle (x+1)^{2}=3\!}$
${\displaystyle x+1=\pm {\sqrt {3}}\!}$

${\displaystyle x=-1\pm {\sqrt {3}}\!}$

إشارة المميز

نعتبر المعادلة ${\displaystyle ax^{2}+bx+c=0\;}$

حيث ${\displaystyle a}$ و${\displaystyle b}$ و${\displaystyle c}$ أعداد حقيقة و${\displaystyle a\neq 0}$.

مميز المعادلة التربيعية هو العدد ${\displaystyle \Delta }$ الذي يحسب بالعلاقة: ${\displaystyle \Delta =b^{2}-4ac\;}$

تحسب قيمة جذور المعادلة استنادا إلى قيمة المميز ${\displaystyle \Delta }$:

• إذا كان ${\displaystyle (\Delta >0)}$ ، فالمعادلة لها حلان حقيقيان مختلفان:

${\displaystyle x_{1}={\frac {-b-{\sqrt {\Delta }}}{2a}}\quad {\text{,}}\quad x_{2}={\frac {-b+{\sqrt {\Delta }}}{2a}}}$

• إذا كان ${\displaystyle (\Delta =0)}$، فالمعادلة لها حل حقيقي واحد مضاعف:

${\displaystyle x_{1}=x_{2}=-{\frac {b}{2a}}\;}$

• إذا كان ${\displaystyle (\Delta <0)}$ فالمعادلة ليس لها حلول حقيقة، بل لها حلان مركبان.

أي دالة تربيعية لها شكل قطع مكافىء، الدالة أعلاه هي f (x) = x² − x − 2 = (x + 1)(x − 2) يتقاطع منحناها مع محور الفواصل في نقطتين هما x = −1 and x = 2، تمثل هاتان النقطتان حلي المعادلة التربيعية x² − x − 2 = 0

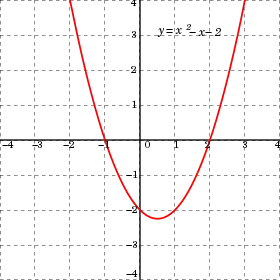
الدوال على الشكل ${\displaystyle f(x)=ax^{2}+bx+c=0\;}$ تسمى دوال تربيعية.

جميع الدوال التربيعية لها شكل عام متشابه يسمى القطع المكافىء، موقع وحجم المقطع يرتبط بالقيم ${\displaystyle a}$ ، ${\displaystyle b}$ ، ${\displaystyle c}$.

إذا كان ${\displaystyle a<0}$ فإن المقطع تكون له قيمة أعظمية كبرى وشكله يكون منفتحا نحو الأسفل، أما إذا كان ${\displaystyle a>0}$ فإن المقطع تكون له قيمة أعظمية صغرى وشكله يكون منفتحا نحو الأعلى.

فاصلة النقطة الأعظية (سواء كبرى أو صغرى) هي النقطة ${\displaystyle x=-{\frac {b}{2a}}\;}$، أما ترتيبتها فنحصل عليها بتعويض قيمة ${\displaystyle x}$ في عبارة الدالة.

حلول الدالة التربيعية هي نقاط تلاقي منحنى الدالة مع محور الفواصل ${\displaystyle x}$.