Half-normal distribution
In probability theory and statistics, the half-normal distribution is a special case of the folded normal distribution.
|
Probability density function 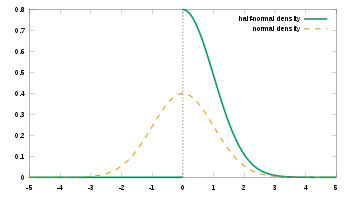 | |||
|
Cumulative distribution function 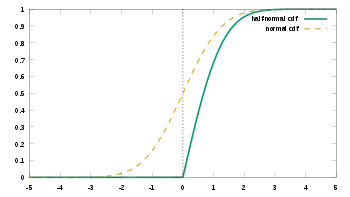 | |||
| Parameters | — (scale) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
Let follow an ordinary normal distribution, . Then, follows a half-normal distribution. Thus, the half-normal distribution is a fold at the mean of an ordinary normal distribution with mean zero.
Properties
Using the parametrization of the normal distribution, the probability density function (PDF) of the half-normal is given by
where .
Alternatively using a scaled precision (inverse of the variance) parametrization (to avoid issues if is near zero), obtained by setting , the probability density function is given by
where .
The cumulative distribution function (CDF) is given by
Using the change-of-variables , the CDF can be written as
where erf is the error function, a standard function in many mathematical software packages.
The quantile function (or inverse CDF) is written:
where and is the inverse error function
The expectation is then given by
The variance is given by
Since this is proportional to the variance σ2 of X, σ can be seen as a scale parameter of the new distribution.
The differential entropy of the half-normal distribution is exactly one bit less the differential entropy of a zero-mean normal distribution with the same second moment about 0. This can be understood intuitively since the magnitude operator reduces information by one bit (if the probability distribution at its input is even). Alternatively, since a half-normal distribution is always positive, the one bit it would take to record whether a standard normal random variable were positive (say, a 1) or negative (say, a 0) is no longer necessary. Thus,
Applications
The half-normal distribution is commonly utilized as a prior probability distribution for variance parameters in Bayesian inference applications.[1][2]
Parameter estimation
Given numbers drawn from a half-normal distribution, the unknown parameter of that distribution can be estimated by the method of maximum likelihood, giving
The bias is equal to
which yields the bias-corrected maximum likelihood estimator
Related distributions
- The distribution is a special case of the folded normal distribution with μ = 0.
- It also coincides with a zero-mean normal distribution truncated from below at zero (see truncated normal distribution)
- If Y has a half-normal distribution, then (Y/σ)2 has a chi square distribution with 1 degree of freedom, i.e. Y/σ has a chi distribution with 1 degree of freedom.
- The half-normal distribution is a special case of the generalized gamma distribution with d = 1, p = 2, a = .
- If Y has a half-normal distribution, Y -2 has a Levy distribution
- The Rayleigh distribution is a moment-tilted and scaled generalization of the half-normal distribution.
- Modified half-normal distribution[3] with the pdf on is given as , where denotes the Fox–Wright Psi function.
See also
References
- Gelman, A. (2006), "Prior distributions for variance parameters in hierarchical models", Bayesian Analysis, 1 (3): 515–534, doi:10.1214/06-ba117a
- Röver, C.; Bender, R.; Dias, S.; Schmid, C.H.; Schmidli, H.; Sturtz, S.; Weber, S.; Friede, T. (2021), "On weakly informative prior distributions for the heterogeneity parameter in Bayesian random‐effects meta‐analysis", Research Synthesis Methods, 12 (4): 448–474, arXiv:2007.08352, doi:10.1002/jrsm.1475, PMID 33486828, S2CID 220546288
- Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). "The Modified-Half-Normal distribution: Properties and an efficient sampling scheme". Communications in Statistics - Theory and Methods. 52 (5): 1591–1613. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
Further reading
- Leone, F. C.; Nelson, L. S.; Nottingham, R. B. (1961), "The folded normal distribution", Technometrics, 3 (4): 543–550, doi:10.2307/1266560, hdl:2027/mdp.39015095248541, JSTOR 1266560