Wigner semicircle distribution
The Wigner semicircle distribution, named after the physicist Eugene Wigner, is the probability distribution on [−R, R] whose probability density function f is a scaled semicircle (i.e., a semi-ellipse) centered at (0, 0):
|
Probability density function 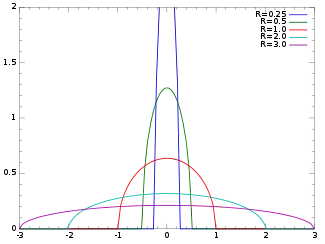 | |||
|
Cumulative distribution function 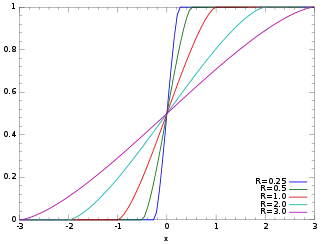 | |||
| Parameters | radius (real) | ||
|---|---|---|---|
| Support | |||
| CDF |
for | ||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
for −R ≤ x ≤ R, and f(x) = 0 if |x| > R. The parameter R is commonly referred to as the "radius" parameter of the distribution.
The Wigner distribution also coincides with a scaled beta distribution. That is, if Y is a beta-distributed random variable with parameters α = β = 3/2, then the random variable X = 2RY – R exhibits a Wigner semicircle distribution with radius R.
The distribution arises as the limiting distribution of the eigenvalues of many random symmetric matrices, that is, as the dimensions of the random matrix approach infinity. The distribution of the spacing or gaps between eigenvalues is addressed by the similarly named Wigner surmise.
General properties
The Chebyshev polynomials of the third kind are orthogonal polynomials with respect to the Wigner semicircle distribution.
For positive integers n, the 2n-th moment of this distribution is
where X is any random variable with this distribution and Cn is the nth Catalan number
so that the moments are the Catalan numbers if R = 2. (Because of symmetry, all of the odd-order moments are zero.)
Making the substitution into the defining equation for the moment generating function it can be seen that:
which can be solved (see Abramowitz and Stegun §9.6.18) to yield:
where is the modified Bessel function. Similarly, the characteristic function is given by:[1][2][3]
where is the Bessel function. (See Abramowitz and Stegun §9.1.20), noting that the corresponding integral involving is zero.)
In the limit of approaching zero, the Wigner semicircle distribution becomes a Dirac delta function.
Relation to free probability
In free probability theory, the role of Wigner's semicircle distribution is analogous to that of the normal distribution in classical probability theory. Namely, in free probability theory, the role of cumulants is occupied by "free cumulants", whose relation to ordinary cumulants is simply that the role of the set of all partitions of a finite set in the theory of ordinary cumulants is replaced by the set of all noncrossing partitions of a finite set. Just as the cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is normal, so also, the free cumulants of degree more than 2 of a probability distribution are all zero if and only if the distribution is Wigner's semicircle distribution.
Related distributions
Wigner (spherical) parabolic distribution
| Parameters | radius (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| MGF | |||
| CF | |||
The parabolic probability distribution supported on the interval [−R, R] of radius R centered at (0, 0):
for −R ≤ x ≤ R, and f(x) = 0 if |x| > R.
Example. The joint distribution is
Hence, the marginal PDF of the spherical (parametric) distribution is:[4]
such that R=1
The characteristic function of a spherical distribution becomes the pattern multiplication of the expected values of the distributions in X, Y and Z.
The parabolic Wigner distribution is also considered the monopole moment of the hydrogen like atomic orbitals.
Wigner n-sphere distribution
The normalized N-sphere probability density function supported on the interval [−1, 1] of radius 1 centered at (0, 0):
,
for −1 ≤ x ≤ 1, and f(x) = 0 if |x| > 1.
Example. The joint distribution is
Hence, the marginal PDF distribution is [4]
such that R=1
The cumulative distribution function (CDF) is
such that R=1 and n >= -1
The characteristic function (CF) of the PDF is related to the beta distribution as shown below
In terms of Bessel functions this is
Raw moments of the PDF are
Central moments are
The corresponding probability moments (mean, variance, skew, kurtosis and excess-kurtosis) are:
Raw moments of the characteristic function are:
For an even distribution the moments are [5]
Hence, the moments of the CF (provided N=1) are
Skew and Kurtosis can also be simplified in terms of Bessel functions.
The entropy is calculated as
The first 5 moments (n=-1 to 3), such that R=1 are
N-sphere Wigner distribution with odd symmetry applied
The marginal PDF distribution with odd symmetry is [4]
such that R=1
Hence, the CF is expressed in terms of Struve functions
"The Struve function arises in the problem of the rigid-piston radiator mounted in an infinite baffle, which has radiation impedance given by" [6]
Example (Normalized Received Signal Strength): quadrature terms
The normalized received signal strength is defined as
and using standard quadrature terms
Hence, for an even distribution we expand the NRSS, such that x = 1 and y = 0, obtaining
The expanded form of the Characteristic function of the received signal strength becomes [7]
See also
- Wigner surmise
- The Wigner semicircle distribution is the limit of the Kesten–McKay distributions, as the parameter d tends to infinity.
- In number-theoretic literature, the Wigner distribution is sometimes called the Sato–Tate distribution. See Sato–Tate conjecture.
- Marchenko–Pastur distribution or Free Poisson distribution
References
- Buchanan, Kristopher; Flores, Carlos; Wheeland, Sara; Jensen, Jeffrey; Grayson, David; Huff, Gregory (2017). "Transmit beamforming for radar applications using circularly tapered random arrays". 2017 IEEE Radar Conference (Radar Conf). pp. 0112–0117. doi:10.1109/RADAR.2017.7944181. ISBN 978-1-4673-8823-8. S2CID 38429370.
- Ryan, Buchanan (29 May 2014). Theory and Applications of Aperiodic (Random) Phased Arrays (Thesis). hdl:1969.1/157918.
- Overturf, Drew; Buchanan, Kristopher; Jensen, Jeffrey; Wheeland, Sara; Huff, Gregory (2017). "Investigation of beamforming patterns from volumetrically distributed phased arrays". MILCOM 2017 - 2017 IEEE Military Communications Conference (MILCOM). pp. 817–822. doi:10.1109/MILCOM.2017.8170756. ISBN 978-1-5386-0595-0. S2CID 11591305. https://ieeexplore.ieee.org/abstract/document/8170756/
- Buchanan, K.; Huff, G. H. (July 2011). "A comparison of geometrically bound random arrays in euclidean space". 2011 IEEE International Symposium on Antennas and Propagation (APSURSI). pp. 2008–2011. doi:10.1109/APS.2011.5996900. ISBN 978-1-4244-9563-4. S2CID 10446533.
- Thomas M. Cover (1963). "Antenna pattern distribution from random array" (PDF) (MEMORANDUM RM-3502--PR). Santa Monica: The RAND Corporation. Archived (PDF) from the original on September 4, 2021.
- W., Weisstein, Eric. "Struve Function". mathworld.wolfram.com. Retrieved 2017-07-28.
{{cite web}}: CS1 maint: multiple names: authors list (link) - "Advanced Beamforming for Distributed and Multi-Beam Networks" (PDF).
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.
External links
- Eric W. Weisstein et al., Wigner's semicircle