Burr distribution
In probability theory, statistics and econometrics, the Burr Type XII distribution or simply the Burr distribution[2] is a continuous probability distribution for a non-negative random variable. It is also known as the Singh–Maddala distribution[3] and is one of a number of different distributions sometimes called the "generalized log-logistic distribution".
|
Probability density function 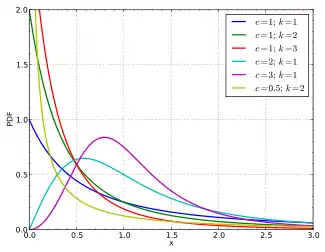 | |||
|
Cumulative distribution function 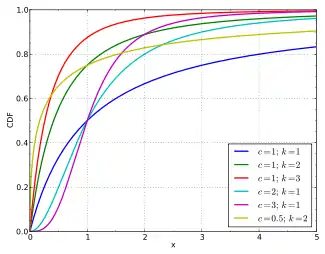 | |||
| Parameters |
| ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | where Β() is the beta function | ||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | where moments (see) | ||
| CF |
where is the Gamma function and is the Fox H-function.[1] | ||
Definitions
Probability density function
The Burr (Type XII) distribution has probability density function:[4][5]
The parameter scales the underlying variate and is a positive real.
Applications
It is most commonly used to model household income, see for example: Household income in the U.S. and compare to magenta graph at right.
Random variate generation
Given a random variable drawn from the uniform distribution in the interval , the random variable
has a Burr Type XII distribution with parameters , and . This follows from the inverse cumulative distribution function given above.
Related distributions
- When c = 1, the Burr distribution becomes the Pareto Type II (Lomax) distribution.
- When k = 1, the Burr distribution is a log-logistic distribution sometimes referred to as the Fisk distribution, a special case of the Champernowne distribution.[6][7]
- The Burr Type XII distribution is a member of a system of continuous distributions introduced by Irving W. Burr (1942), which comprises 12 distributions.[8]
- The Dagum distribution, also known as the inverse Burr distribution, is the distribution of 1 / X, where X has the Burr distribution
References
- Nadarajah, S.; Pogány, T. K.; Saxena, R. K. (2012). "On the characteristic function for Burr distributions". Statistics. 46 (3): 419–428. doi:10.1080/02331888.2010.513442.
- Burr, I. W. (1942). "Cumulative frequency functions". Annals of Mathematical Statistics. 13 (2): 215–232. doi:10.1214/aoms/1177731607. JSTOR 2235756.
- Singh, S.; Maddala, G. (1976). "A Function for the Size Distribution of Incomes". Econometrica. 44 (5): 963–970. doi:10.2307/1911538. JSTOR 1911538.
- Maddala, G. S. (1996) [1983]. Limited-Dependent and Qualitative Variables in Econometrics. Cambridge University Press. ISBN 0-521-33825-5.
- Tadikamalla, Pandu R. (1980), "A Look at the Burr and Related Distributions", International Statistical Review, 48 (3): 337–344, doi:10.2307/1402945, JSTOR 1402945
- C. Kleiber and S. Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. New York: Wiley. See Sections 7.3 "Champernowne Distribution" and 6.4.1 "Fisk Distribution."
- Champernowne, D. G. (1952). "The graduation of income distributions". Econometrica. 20 (4): 591–614. doi:10.2307/1907644. JSTOR 1907644.
- See Kleiber and Kotz (2003), Table 2.4, p. 51, "The Burr Distributions."
Further reading
- Rodriguez, R. N. (1977). "A guide to Burr Type XII distributions". Biometrika. 64 (1): 129–134. doi:10.1093/biomet/64.1.129.
External links
- John (2023-02-16). "The other Burr distributions". www.johndcook.com.